解决CRIC算法难题：递归与迭代的深度剖析（专家解读）

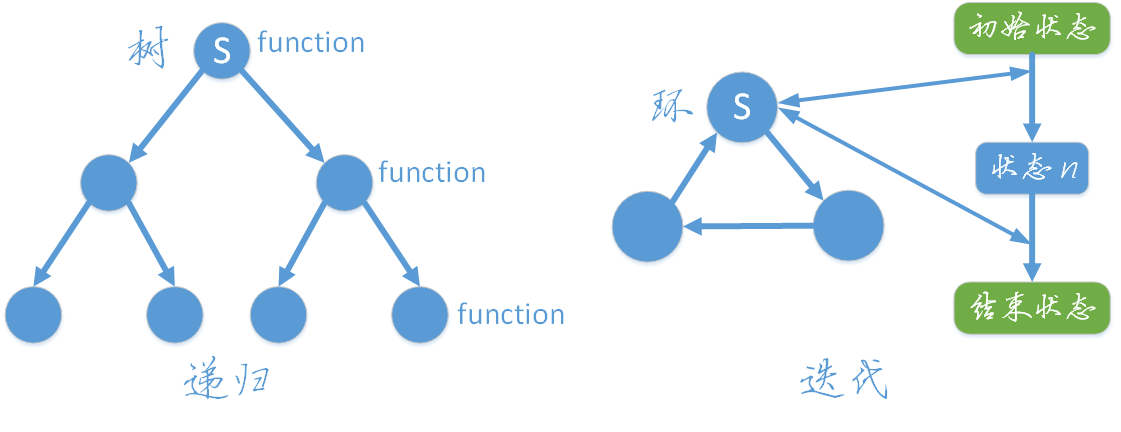
# 1. CRIC算法简介

CRIC（Combinatorial Recursion and Iteration Comparison）算法是计算机科学中的一种重要算法。它以递归和迭代为核心，通过对比和分析两者的性能和适用场景，为解决实际问题提供参考。CRIC算法能够将复杂问题拆分为简单问题，并通过递归和迭代的相互作用，找到最优解。

CRIC算法的应用广泛，无论是在排序算法、搜索算法，还是在复杂系统的设计和优化中，都能看到CRIC算法的影子。因此，深入理解CRIC算法，能够帮助我们更好地理解和掌握计算机程序设计的核心思想。

# 2. 理解递归

## 2.1 递归的概念和原理
### 2.1.1 递归的定义
递归是一种常见的编程技术，它允许函数调用自身来解决问题。其核心思想是将大问题分解为相似的小问题，直至达到一个简单到可以直接解决的规模。递归通常涉及到两个主要部分：基本情况（base case）和递归情况（recursive case）。基本情况是递归的终止点，通常是问题的最简单实例；递归情况则将问题分解为更小的实例，并递归地调用自身。

### 2.1.2 递归的工作机制
递归工作时，每次函数调用都会进入一个自己的上下文环境。这些上下文环境被压入调用栈（call stack），形成一个“调用栈帧”（stack frame）。随着递归调用的深入，新的栈帧会不断地加入到栈顶，直至达到基本情况，此时栈帧开始一个接一个地弹出，返回前一个栈帧，直至最初调用的栈帧，整个递归过程结束。

## 2.2 递归的实现方式
### 2.2.1 基本递归结构
一个基本的递归结构由两个部分组成：基本情况和递归步骤。以下是一个递归函数的基本模板：

def recursive_function(parameters):
    if base_condition:  # 基本情况
        return base_case_result
    else:
        # 递归步骤，通常包含对函数自身的调用
        return recursive_function(modified_parameters)

递归函数应始终朝着基本情况的方向进展，否则可能导致无限递归，最终导致栈溢出错误。

### 2.2.2 递归的终止条件
为了确保递归能够正常结束，必须设置正确的终止条件。这个条件能够确保每次递归调用都比上一次更接近基本情况。终止条件是递归能够正确工作的关键。在设计递归函数时，需要仔细考虑这个条件，以防止死循环的发生。

## 2.3 递归的实例分析
### 2.3.1 简单的递归实例
考虑一个简单的递归问题：计算阶乘。

def factorial(n):
    # 基本情况
    if n == 1:
        return 1
    # 递归步骤
    else:
        return n * factorial(n-1)

在上面的例子中，`n == 1` 是基本情况，而 `factorial(n-1)` 是递归步骤。每次递归调用都会减少 `n` 的值，直至 `n` 达到 1。

### 2.3.2 复杂递归问题解决
对于更复杂的问题，如遍历树结构，递归可以很自然地进行深度优先搜索（DFS）。假设我们有一个二叉树节点的定义：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

现在我们想要通过递归的方式遍历整个树并打印节点的值：

def traverse_tree(node):
    if node is not None:
        print(node.val)           # 访问当前节点
        traverse_tree(node.left)  # 遍历左子树
        traverse_tree(node.right) # 遍历右子树

上述代码递归地访问每个节点，按照深度优先的方式深入到树的最左节点，然后回溯到上一个节点，并继续深入右子树。

通过本章节的介绍，我们已经了解了递归的基本概念、实现方式以及实例分析。在下一章中，我们将对比递归与迭代，探讨它们的不同和各自的适用场景。

# 3. 理解迭代

理解迭代是计算机科学和编程实践中的一项基本技能。迭代是一种常用的算法设计范式，它通过重复应用相同的操作来解决问题。与递归相比，迭代通常更节省内存，因为它避免了重复函数调用导致的栈空间使用。本章节将深入探讨迭代的基本概念、实现技术和应用实例。

## 3.1 迭代的基本概念

迭代的定义和与递归的区别是理解迭代的第一步。接下来将详细解释这两个子章节的内容。

### 3.1.1 迭代的定义

迭代是一种问题解决方法，它重复地执行一系列操作，直到达到预定的目标或满足终止条件为止。在编程中，迭代通常使用循环结构实现，如`for`循环、`while`循环等。

在迭代过程中，我们通常维护一个或多个状态变量，它们在每次迭代中根据给定的逻辑进行更新，直到达到某个条件，迭代过程结束。

# 示例：使用Python中的while循环进行迭代

# 初始条件
number = 1
# 终止条件
max_number = 5

# 迭代过程
while number <= max_number:
    print(number)  # 打印当前数字
    number += 1  # 更新状态变量
# 迭代结束条件满足时退出循环

在上述Python代码中，我们通过`while`循环迭代变量`number`从1增加到5。

### 3.1.2 迭代与递归的区别

迭代和递归是两种不同的算法设计模式。它们各有优缺点，并在不同的场景下有着不同的适用性。理解它们之间的区别有助于选择最合适的解决问题的方法。

- **资源使用**：迭代通常比递归更节省内存，因为它不涉及额外的函数调用开销，不需要为每一次递归调用分配新的栈帧。
- **执行过程**：递归是自顶向下的解决问题方式，而迭代则是自底向上，通常更为直观。
- **代码可读性**：递归代码通常更简洁明了，但可能需要额外的理解来处理递归的终止条件和返回值。
- **适用范围**：对于某些特定问题，如树或图的遍历，递归可能更加直观易写；而对于可以明确迭代次数的问题，迭代可能更加高效。

## 3.2 迭代的实现技术

实现迭代的关键在于选择合适的循环结构以及有效地管理状态变量。本节将探讨循环结构的使用和迭代中的状态管理。

### 3.2.1 循环结构的使用

在不同的编程语言中，循环结构的语法和功能可能有所不同，但其核心概念基本相同。循环结构使得我们能够重复执行一段代码直到满足特定条件。

常见的循环结构有：

- `for`循环：用于遍历集合（如数组、列表）或重复执行特定次数。
- `while`循环：基于条件的循环，直到给定条件不再满足。

// 示例：C语言中的for循环使用

#include <stdio.h>

int main() {
    int i;
    for (i = 1; i <= 5; i++) {
        printf("%d\n", i);  // 输出1到5
    }
    return 0;
}

在C语言中，`for`循环是一种常见的迭代方式。

### 3.2.2 迭代中的状态管理

迭代中的状态管理指的是如何跟踪和更新那些在每次迭代中可能变化的变量。状态变量可以是一个简单的计数器，也可以是更复杂的数据结