复数虚部在控制理论中的应用：探索虚数在控制理论中的作用

# 1. 复数基础**

复数是具有实部和虚部的数学对象，表示为 a + bi，其中 a 和 b 是实数，i 是虚数单位，满足 i² = -1。复数可以表示为平面上的点，实部是 x 坐标，虚部是 y 坐标。

复数运算遵循与实数类似的规则，但增加了虚数单位 i 的乘法运算。复数的加法、减法和乘法与实数相同，而除法则需要使用复数共轭。复数共轭是将虚部取相反数，例如 (a + bi)* = a - bi。

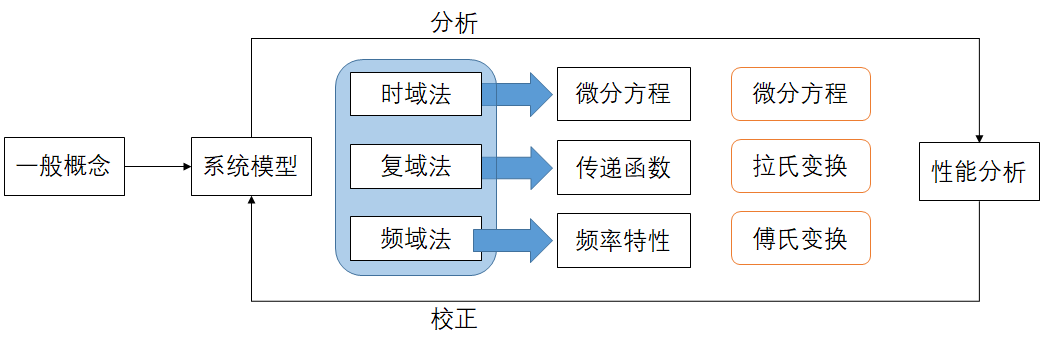
复数在控制理论中具有重要意义，因为它允许使用正弦和余弦函数来表示时变信号。在控制系统中，信号通常是时间函数，复数可以方便地表示这些信号的幅度和相位信息。

# 2. 复数在控制理论中的应用**

复数在控制理论中扮演着至关重要的角色，为时域和频域分析以及控制系统设计提供了强大的工具。

### 2.1 虚数在时域分析中的作用

#### 2.1.1 频率响应分析

复数可以用来分析控制系统的频率响应，它提供了系统对不同频率输入的输出响应。通过傅里叶变换，时域信号可以转换为频域信号，其中复数用于表示幅度和相位信息。

import numpy as np
import matplotlib.pyplot as plt

# 定义时域信号
t = np.linspace(0, 1, 1000)
x = np.sin(2 * np.pi * 10 * t)

# 傅里叶变换
X = np.fft.fft(x)

# 计算幅度和相位
amplitude = np.abs(X)
phase = np.angle(X)

# 绘制幅度和相位响应
plt.figure()
plt.subplot(2, 1, 1)
plt.plot(t, amplitude)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.subplot(2, 1, 2)
plt.plot(t, phase)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Phase')
plt.show()

**代码逻辑解读：**

* `np.fft.fft(x)`：执行傅里叶变换，将时域信号转换为频域信号。
* `np.abs(X)`：计算频域信号的幅度。
* `np.angle(X)`：计算频域信号的相位。
* `plt.plot(t, amplitude)`：绘制幅度响应。
* `plt.plot(t, phase)`：绘制相位响应。

#### 2.1.2 稳定性分析

复数还可用于分析控制系统的稳定性。奈奎斯特稳定性判据利用复数平面上的奈奎斯特图来确定系统是否稳定。奈奎斯特图绘制了开环传递函数在复数平面上的轨迹，如果轨迹不包围原点，则系统稳定。

import control
import numpy as np

# 定义传递函数
num = [1]
den = [1, 2, 1]
G = control.TransferFunction(num, den)

# 计算奈奎斯特图
w = np.logspace(-3, 3, 1000)
G_jw = G.freqresp(w)