无监督学习案例全解析：如何从零开始构建聚类模型

# 1. 无监督学习与聚类分析概述

在机器学习领域，无监督学习是第二大重要的研究和应用方向。在众多的无监督学习方法中，聚类分析作为最为核心的技术之一，已经广泛应用于数据挖掘、模式识别、图像处理、生物信息学、市场营销等多个领域。聚类分析的核心思想在于将数据集中的样本划分为若干个类别，使得同一类别内的样本尽可能相似，而不同类别间的样本则尽可能相异。

在本章中，我们将介绍无监督学习与聚类分析的基本概念，对比其与监督学习的不同，并探讨聚类分析的主要应用场景。通过对这些基础知识的了解，读者将为后续章节中深入探讨聚类算法和实战应用打下坚实的基础。

下面是一个简单而直接的代码示例，展示了如何使用Python的scikit-learn库来实现一个基本的K-means聚类分析过程：

from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 创建一个模拟数据集
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=0.60, random_state=0)

# 实例化KMeans聚类算法，并指定簇的数量
kmeans = KMeans(n_clusters=3)

# 进行聚类
kmeans.fit(X)

# 打印聚类结果
print(kmeans.labels_)

在上述代码中，我们首先使用`make_blobs`函数生成了一个模拟的二类数据集。接着，我们实例化了一个`KMeans`聚类器对象，并设定我们期望的簇数量为3。通过调用`fit`方法，数据集`X`被用来训练模型，并且我们可以打印出每个样本点对应的簇标签。这个过程是聚类分析中极为常见的一个入门级案例。

# 2. 理论基础与数学原理

在这一章节中，我们深入探讨无监督学习的理论基础与数学原理，为理解后续的聚类算法和模型构建打下坚实的基础。

## 2.1 无监督学习的定义与特点
### 2.1.1 与监督学习的比较
无监督学习与监督学习在机器学习领域是两种截然不同的方法。监督学习依赖于标注数据集，模型通过已知输入和对应输出的大量样本，学习得到一个映射关系，用以预测未知数据的输出。而无监督学习则不依赖于标注数据，它试图在没有预定义标签的情况下从输入数据中发现隐藏的结构或模式。

在无监督学习中，模型的目标是探索数据的内在分布，最典型的任务是聚类分析，即将数据根据相似性划分为多个簇。例如，无监督学习可以应用于市场细分，根据消费者购买行为来发现不同的消费群体。

### 2.1.2 无监督学习的应用场景
无监督学习的应用场景十分广泛，尤其在数据预处理和探索性数据分析中扮演重要角色。以下是无监督学习常见的一些应用场景：

- **数据挖掘**：通过聚类分析，可以发现隐藏在大量数据中的模式和关系。
- **异常检测**：无监督学习可以识别出数据中的异常点或离群值。
- **推荐系统**：例如，通过用户的购买历史进行聚类，从而为用户推荐可能感兴趣的产品。
- **特征学习**：降维技术如主成分分析（PCA）属于无监督学习，可以减少数据的维度，同时保留大部分信息。

## 2.2 聚类分析的数学基础
### 2.2.1 距离度量方法
在进行聚类之前，我们必须定义数据点之间的相似性或距离。距离度量是聚类分析的核心，它直接影响聚类结果的质量。常见的距离度量方法包括：

- **欧氏距离**：最常见的距离度量方式，适用于连续型变量。

  def euclidean_distance(point1, point2):
      return np.sqrt(np.sum((point1 - point2)**2))

- **曼哈顿距离**：适用于需要限制移动方向的场景。

  def manhattan_distance(point1, point2):
      return np.sum(np.abs(point1 - point2))

- **余弦相似度**：常用于高维文本数据，衡量的是两个向量的角度而非绝对距离。

### 2.2.2 聚类有效性指标
聚类结果的质量评估是聚类分析中至关重要的一环。有效性指标帮助我们量化聚类结果的好坏。一些常用的聚类有效性指标有：

- **轮廓系数（Silhouette Coefficient）**：综合考虑了聚类的紧密度和分离度，值越接近1，说明聚类效果越好。
- **Davies-Bouldin指数**：通过比较簇内散度与簇间散度的比率来评估聚类效果。
- **Calinski-Harabasz指数**：衡量聚类后的类内离散度与类间离散度的比率。

## 2.3 聚类算法的分类与原理
### 2.3.1 基于划分的方法
基于划分的聚类方法需要预先定义聚类的数目。其中最著名的是K-means算法。K-means的目标是将数据点分成K个簇，使得簇内的点尽量紧凑，簇间点尽量远离。以下是K-means算法的核心步骤：

1. **初始化**：随机选择K个数据点作为初始簇中心。
2. **分配**：将每个数据点分配到最近的簇中心。
3. **更新**：重新计算每个簇的中心。
4. **迭代**：重复步骤2和步骤3直到满足某个终止条件。

from sklearn.cluster import KMeans

# 示例代码
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
labels = kmeans.labels_

### 2.3.2 基于层次的方法
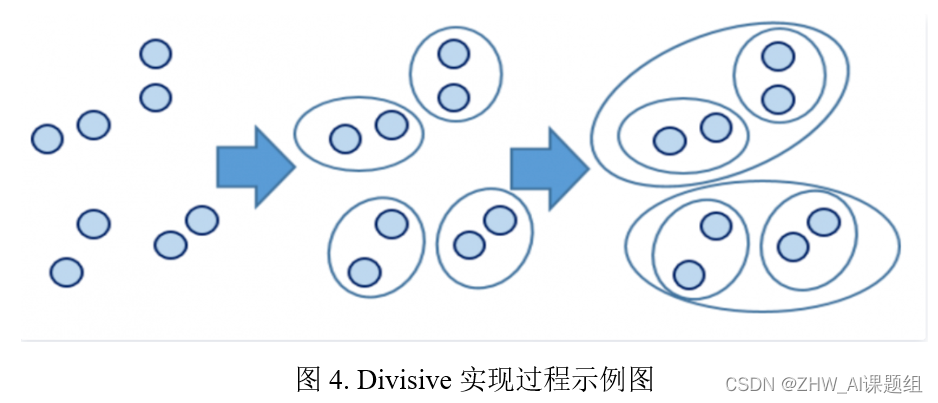
基于层次的聚类算法构建了一个聚类的层次树（dendrogram），在树的不同层次上可以得到不同的聚类结果。层次聚类可以分为凝聚式和分裂式两种：

- **凝聚式（Agglomerative）**：自下而上的策略，最初将每个点视为一个簇，逐步合并相似的簇，直到达到预设的簇数。
- **分裂式（Divisive）**：自上而下的策略，最初将所有数据点归为一个簇，然后迭代地将簇拆分成更小的簇。

### 2.3.3 基于密度的方法
基于密度的聚类方法如DBSCAN，通过寻找数据中的高密度区域将点聚类在一起。高密度区域通过邻域内点的数目来定义。DBSCAN算法的核心思想是，一个聚类被定义为密度相连的点的最大集合，且所有点都位于某个阈值距离内的核心点。

DBSCAN算法的两个主要参数是：
- `eps`：邻域半径，用于定义邻域内点的范围。
- `min_samples`：核心点所需的邻域内点数。

from sklearn.cluster import DBSCAN

dbscan = DBSCAN(eps=0.3, min_samples=10).fit(X)
labels = dbscan.labels_

在本章节中，我们对无监督学习和聚类分析的理论基础与数学原理进行了详细阐述。我们比较了无监督学习与监督学习的不同，探讨了距离度量方法和聚类有效性指标，并且分别介绍了基于划分、层次和密度的聚类方法。这些理论知识为后面章节中聚类模型的构建和评估奠定了基础。在下一章中，我们将进一步深入数据预处理、模型的选择与实现，以及模型评估与优化的讨论。

# 3. 聚类模型的构建与评估

## 3.1 数据预处理

数据预处理是机器学习中至关重要的一步，对于聚类分析也不例外。聚类的效果很大程度上取决于数据的质量和处理方式。以下是数据预处理的两个主要方面：数据清洗和特征选择与提取。

### 3.1.1 数据清洗

数据清洗的目的是发现并纠正数据集中的错误或异常值，提高数据质量。常见的数据清洗步骤包括处理缺失值、异常值检测和处理重复记录。

**代码块示例**:

import pandas as pd

# 示例数据
data = pd.DataFrame({
    'feature_1': [1, 2, None, 4, 5],
    'feature_2': [2, 3, 4, 5, None],
    'label': ['A', 'B', 'B', 'A', 'C']
})

# 处理缺失值
data = data.dropna()

# 异常值检测与处理
for col in data.columns:
    mean = data[col].mean()
    std = data[col].std()
    data = data[(data[col] > mean - 3 * std) & (data[col] < mean + 3 * std)]

# 处理重复记录
data = data.drop_duplicates()

print(data)

逻辑分析与参数说明:
- 在处理缺失值时，我们使用 `dropna()` 方法来删除含有缺失值的行。
-