无监督学习精粹：时间序列分析的7个高阶应用

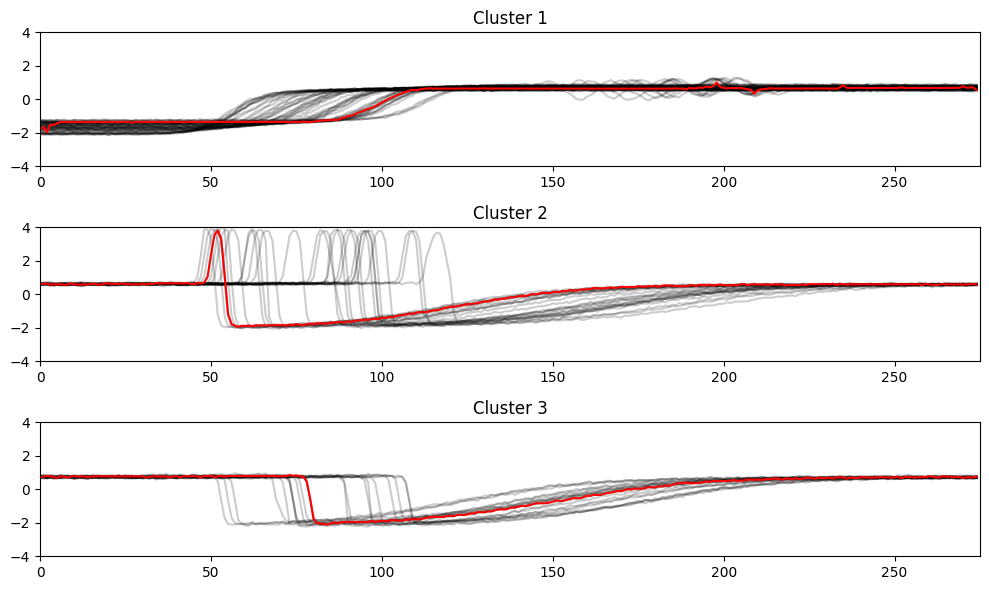
# 1. 无监督学习与时间序列分析基础

在开始时间序列分析之前，需要了解无监督学习的核心概念，为深入理解后续章节打下基础。无监督学习的目标是从未标记的数据中发现结构、模式和关系，无需依赖预先标记的训练数据集。**时间序列分析**作为一种特定类型的数据分析，专注于对按时间顺序排列的数据点进行分析，以识别其中的趋势、季节性、周期性和异常值。由于其有序性，时间序列分析往往与无监督学习中的一些算法，如聚类和关联规则挖掘，紧密相连。

时间序列分析的关键在于理解数据的内在模式，以便进行准确的预测和决策。在应用任何高级技术之前，重要的是首先掌握无监督学习的基本原理，这将为进一步的特征提取、聚类分析、预测模型构建等奠定坚实的基础。

接下来，我们将通过实例和理论探讨，逐步深入了解时间序列分析的各个重要组成部分。在此过程中，我们会涉及统计学、机器学习以及数据可视化等多方面的知识，以期能全面掌握时间序列分析的艺术和科学。

# 2. 时间序列的特征提取技术

## 2.1 时间序列数据的预处理

### 2.1.1 数据清洗

在时间序列分析的初期阶段，数据清洗是一个至关重要的步骤。这一步骤涉及识别和修正数据集中的错误和不一致性，以确保数据的质量。数据清洗过程包括处理缺失值、去除噪声和异常值、以及识别和纠正数据输入错误。例如，你可能会发现有些数据点是异常的，因为它们远远偏离了数据集的正常范围，或者它们是重复的，这都需要通过适当的技术来修正或删除。

import pandas as pd

# 假设df是包含时间序列数据的DataFrame
# 检查缺失值
df.isnull().sum()

# 处理缺失值，这里选择用前后值填充（前向填充，后向填充）
df.fillna(method='ffill', inplace=True)
df.fillna(method='bfill', inplace=True)

# 删除重复数据
df.drop_duplicates(inplace=True)

代码解释：`fillna`方法用前一个非空值（前向填充）和后一个非空值（后向填充）来填补缺失值。`drop_duplicates`方法删除重复的数据。

### 2.1.2 数据标准化与归一化

数据标准化和归一化是预处理步骤中的关键部分，它们的目的是将数据的分布缩放到一个特定的范围。标准化通常将数据缩放到具有零均值和单位方差，而归一化通常将数据缩放到一个特定的范围，如0到1。这一步骤对减少数据的偏度和方差非常有帮助，从而改善学习算法的性能。

from sklearn.preprocessing import StandardScaler, MinMaxScaler

# 假设df['value']是需要标准化或归一化的数据列
scaler = StandardScaler()
df['value_scaled'] = scaler.fit_transform(df[['value']])

scaler = MinMaxScaler(feature_range=(0, 1))
df['value_normalized'] = scaler.fit_transform(df[['value']])

代码逻辑分析：这里我们使用了`StandardScaler`和`MinMaxScaler`两种不同的缩放器，分别对应数据的标准化和归一化。`fit_transform`方法首先拟合数据，然后应用转换。

## 2.2 时间序列特征的计算方法

### 2.2.1 统计特征提取

统计特征是时间序列分析中提取特征的简单且有效的方法。常见的统计特征包括均值、中位数、标准差、偏度和峰度等。这些特征能够提供时间序列数据的概括性描述，并用于进一步的分析和模型构建。

import numpy as np

# 计算统计特征
mean_value = np.mean(df['value_scaled'])
median_value = np.median(df['value_scaled'])
std_dev = np.std(df['value_scaled'])
skewness = df['value_scaled'].skew()
kurtosis = df['value_scaled'].kurt()

# 输出特征值
print(f"均值: {mean_value}, 中位数: {median_value}, 标准差: {std_dev}, 偏度: {skewness}, 峰度: {kurtosis}")

代码扩展性说明：此代码块计算了缩放后的数据列的几个关键统计特征，并打印出来。这些特征可以用于了解时间序列数据的分布特性，并用于模式识别、异常检测和预测模型的训练。

### 2.2.2 基于傅里叶变换的特征提取

傅里叶变换是另一种强大的特征提取方法，它能够揭示时间序列数据中的周期性成分。通过傅里叶变换，可以将时间域的数据转换为频域，从而识别和利用时间序列数据的周期性模式。

from scipy.fft import fft

# 假设df['value']是时间序列数据
# 对数据进行傅里叶变换
fft_values = fft(df['value'])

# 提取傅里叶特征
fft_features = np.abs(fft_values)  # 取模得到幅度谱
fft_freq = np.fft.fftfreq(len(fft_features), d=1)  # 计算频率

# 打印傅里叶特征
print("傅里叶特征:", fft_features)

代码逻辑分析：`fft`方法进行傅里叶变换，`np.abs`计算复数的绝对值，即得到频率域的幅度谱，这是最重要的傅里叶特征。`np.fft.fftfreq`用于计算频率分量。

## 2.3 特征选择与降维技术

### 2.3.1 主成分分析（PCA）

主成分分析（PCA）是一种有效的降维技术，它通过线性变换将数据转换到一个新坐标系统中，使得数据在新坐标系中的方差最大化。PCA可以用于提取最重要的特征，减少数据集的维度，进而减少模型的计算复杂度并避免过拟合。

from sklearn.decomposition import PCA

# 假设df_features是经过特征提取的时间序列特征集
pca = PCA(n_components=2)
df_pca = pca.fit_transform(df_features)

# 打印主成分分析后的数据
print("PCA后的数据：\n", df_pca)

参数说明：`n_components=2`表示选择保留两个主成分。参数可以根据实际需要进行调整。

### 2.3.2 随机投影与线性判别分析（LDA）

随机投影是另一种降维技术，而线性判别分析（LDA）是一种监督学习的降维技术，它旨在将数据投影到一个较低维的空间中，同时保留类别间的最大可分性。

from sklearn.random_projection import GaussianRandomProjection
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

# 使用随机投影
rp = GaussianRandomProjection(n_components=2)
df_rp = rp.fit_transform(df_features)

# 使用LDA
lda = LDA(n_components=2)
df_lda = lda.fit_transform(df_features, df['target'])

# 打印随机投影和LDA后的数据
print("随机投影后的数据：\n", df_rp)
print("LDA后的数据：\n", df_lda)

代码扩展性说明：在这里，`GaussianRandomProjection`和`LinearDiscriminantAnalysis`分别用于随机投影和LDA降维。`n_components=2`表明目标维度被降为两个，这个值可以根据需要进行调整以达到最优降维效果。

到此为止，我们已经详细探讨了时间序列的特征提取技术，包括数据预处理的两种基本方法，以及特征计算的统计方法和基于傅里叶变换的方法。接着，我们讨论了特征选择和降维技术，包括主成分分析、随机投影和线性判别分析。这些技术共同构成了时间序列分析的基础，为后续的建模和分析工作打下了坚实的基础。在下一章中，我们将深入探讨时间序列的聚类分析，这是一种无监督学习方法，对于发现数据中的模式和关系具有重要的意义。

# 3. 时间序列聚类分析

## 3.1 聚类算法在时间序列中的应用

聚类分析是