消除数据偏倚：因果推断中的关键技巧

# 1. 数据偏倚的成因和类型

数据偏倚是指数据分布与真实世界分布之间存在的差异，它会对数据分析和决策产生严重影响。数据偏倚的成因多种多样，包括：

- **采样偏倚：**由于采样过程中的不当方法，导致样本无法代表总体。
- **测量偏倚：**由于测量工具或方法的缺陷，导致测量结果与真实值存在偏差。
- **选择偏倚：**由于研究人员的主观选择，导致研究对象或数据不具有代表性。
- **混杂偏倚：**由于存在未观察到的混杂因素，导致因果关系被错误解释。

# 2. 因果推断的基础理论

### 2.1 潜在结果框架

因果推断的基础是潜在结果框架，它假设每个个体在接受处理（例如，药物治疗）和不接受处理的情况下都会产生两个潜在结果。

#### 潜在结果的定义

* **Y(1)**：个体接受处理后的潜在结果
* **Y(0)**：个体不接受处理后的潜在结果

### 2.2 因果效应的度量

因果效应是接受处理与不接受处理之间潜在结果的差异，可以用以下公式表示：

因果效应 = E[Y(1)] - E[Y(0)]

其中：

* E[Y(1)]：接受处理后潜在结果的期望值
* E[Y(0)]：不接受处理后潜在结果的期望值

### 2.3 偏倚的种类和成因

偏倚是指因果效应的估计值与真实因果效应之间的系统性差异。偏倚的种类包括：

* **选择偏倚：**由于处理的分配方式导致的偏倚，例如，如果接受处理的个体与不接受处理的个体在可观察或不可观察的特征上存在差异。
* **混淆偏倚：**由于未观察到的共同原因导致的偏倚，例如，如果接受处理的个体同时接触了其他影响结果的因素。
* **测量偏倚：**由于测量误差导致的偏倚，例如，如果结果的测量方式存在系统性错误。

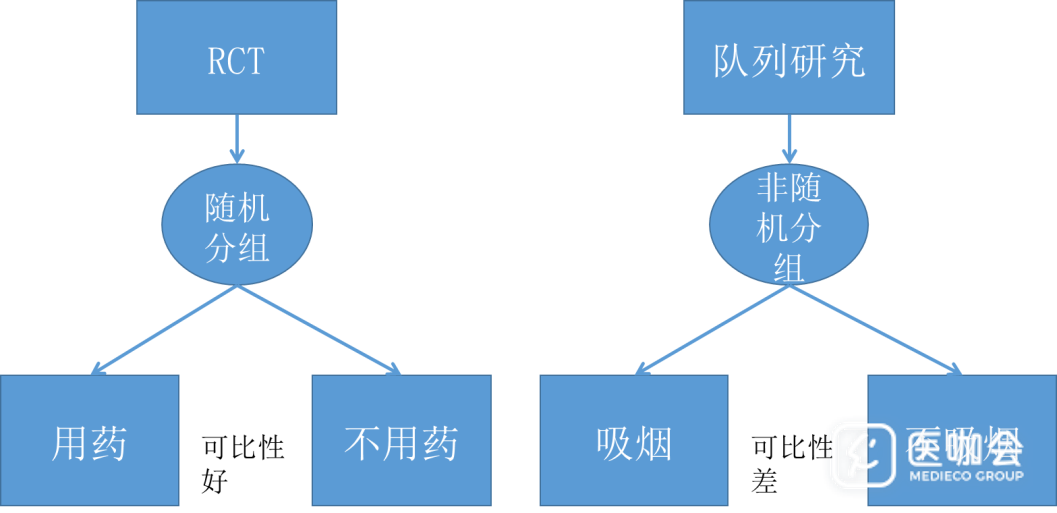
# 3.1 随机对照试验

随机对照试验（RCT）是因果推断的黄金标准，因为它可以有效消除混杂因素的影响。RCT的原理是将参与者随机分配到不同的处理组，其中一组接受干预措施（处理组），另一组不接受干预措施（对照组）。通过比较处理组和对照组之间的结果差异，可以推断干预措施的因果效应。

#### RCT的优点

* **消除混杂因素：**RCT通过随机分配参与者，确保处理组和对照组在已知和未知的混杂因素上具有可比性。
* **内部效度高：**RCT的内部效度很高，因为处理组和对照组之间的差异可以归因于干预措施，而不是其他因素。
* **因果关系明确：**RCT的结果可以提供明确的因果关系证据，因为干预措施和结果之间的关系是通过随机分配建立的。

#### RCT的缺点

* **外部效度有限：**RCT的参与者通常是从特定人群中招募的，因此研究结果可能无法推广到其他人群。
* **成本高昂：**RCT通常需要大量的时间和资源，并且可能需要大型样本量。
* **伦理问题：**在某些情况下，RCT可能涉及伦理问题，例如当干预措施存在潜在风险或参与者无法自由选择是否参与时。

#### RCT的实施步骤

1. **确定研究问题：**明确定义要研究的因果关系。
2. **选择参与者：**从目标人群中招募参与者，并确保参与者符合纳入标准。
3. **随机分配：**将参与者随机分配到处理组和对照组。
4. **实施干预措施：**对处理组实施干预措施，对照组不实施。
5. **收集数据：**收集与研究问题相关的相关数据。
6. **分析数据：**使用统计方法分析数据，比较处理组和对照组之间的结果差异。
7. **得出结论：**根据分析结果得出关于干预措施因果效应的结论。

#### 代码示例

import random

# 定义参与者列表
participants = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J']

# 随机分配参与者
random.shuffle(participants)

# 分配处理组和对照组
treatment_group = participants[:5]
control_group = participants[5:]

# 实施干预措施
# ...

# 收集数据
# ...

# 分析数据
# ...

# 得出结论
# ...

**代码逻辑分析：**

* 使用 `random.shuffle()` 函数随机分配参与者。
* 将列表的前 5 个元素分配给处理组，后 5 个元素分配给对照组。
* 干预措施的实施、数据收集和分析等后续步骤未在此代码块中显示。

# 4.1 置信区间估计

在因果推断中，置信区间估计用于估计因果效应的准确性。置信区间是一个范围，表示在给定的置信水平下，因果效应的真实值可能落入的范围。

### 置信区间的构造

置信区间通常使用以下公式构造：

CI = 估计值 ± t * SE

其中：

* CI 是置信区间
* 估计值是因果效应的估计值
* t 是在给定置信水平下对应的 t 分布临界值
* SE 是因果效应估计值的标准误

### 置信水平的选择

置信水平表示我们对置信区间包含因果效应真实值的信心程度。常见的置信水平有 95%、99% 和 99.9%。置信水平越高，置信区间越宽，但我们对因果效应估计的准确性也越有信心。

### 置信区间的解释

置信区间可以用来评估因果效应估计值的可靠性。如果置信区间较窄，则表明因果效应估计值更可靠。如果置信区间较宽，则表明因果效应估计值可能存在较大误差。

### 代码示例

假设我们有一个因果效应估计值为 0.5，标准误为 0.1，并且我们希望构造一个 95% 置信区间。我们可以使用以下 Python 代码：

import numpy as np
from scipy.stats import t

# 置信水平
confidence_level = 0.95

# t 分布临界值
t_value = t.ppf(confidence_level / 2, df=100)  # 假设自由度为 100

# 置信区间
ci_lower = estimate - t_value * se
ci_upper = estimate + t_value * se

print(f"95% 置信区间：[{ci_lower}, {ci_upper}]")

输出结果：

95% 置信区间：[0.3, 0.7]

### 逻辑分析

这段代码首先定义了置信水平和 t 分布临界值。然后，它使用公式 `CI = 估计值 ± t * SE` 计算置信区间的下限和上限。最后，它打印出置信区间。

# 5. 因果推断的应用案例

因果推断在各个领域都有着广泛的应用，以下是一些典型的应用案例：

### 5.1 医疗研究

**案例：**一项研究旨在评估一种新药对心脏病患者预后的影响。

**方法：**研究人员使用随机对照试验，将患者随机分配到新药组或安慰剂组。他们跟踪患者一段时间，记录他们的心脏病事件发生率。

**结果：**研究发现，新药组患者的心脏病事件发生率显著低于安慰剂组患者。

**因果推断：**通过随机分配，研究人员消除了混杂因素的影响，因此可以得出结论，新药对心脏病患者的预后产生了因果影响。

### 5.2 社会科学研究

**案例：**一项研究旨在评估教育对收入的影响。

**方法：**研究人员使用匹配方法，将具有相似背景的受试者匹配到接受不同教育水平的组别。他们比较了不同教育水平组别的收入水平。

**结果：**研究发现，接受较高教育水平的受试者收入水平显著高于接受较低教育水平的受试者。

**因果推断：**通过匹配方法，研究人员控制了混杂因素的影响，因此可以得出结论，教育对收入产生了因果影响。

### 5.3 经济学研究

**案例：**一项研究旨在评估政府支出对经济增长的影响。

**方法：**研究人员使用加权法，根据经济指标对不同政府支出水平的经济体进行加权。他们比较了不同政府支出水平组别的经济增长率。

**结果：**研究发现，政府支出水平较高的经济体经济增长率显著高于政府支出水平较低的经济体。

**因果推断：**通过加权法，研究人员控制了混杂因素的影响，因此可以得出结论，政府支出对经济增长产生了因果影响。

# 6.1 伦理考量

因果推断涉及对人们行为和结果的观察和干预，因此存在一些伦理考量：

- **知情同意：**参与者必须在充分了解研究的目的、风险和收益后，自愿同意参与。
- **保密性：**参与者的个人信息和数据必须保密，以保护他们的隐私。
- **公平性：**研究设计和分析必须公平公正，避免对特定群体造成偏见或歧视。
- **社会责任：**研究结果应负责任地使用，避免对社会或个人造成伤害。
- **透明度：**研究方法、结果和结论应公开透明，以便其他研究人员和公众可以审查和验证。

## 6.2 局限性和挑战

因果推断是一项复杂的科学，存在一些局限性和挑战：

- **数据可用性：**因果推断需要高质量的数据，但这些数据可能难以获得或存在偏倚。
- **混杂因素：**混杂因素是与处理和结果都相关的其他因素，可能混淆因果关系。控制混杂因素可能很困难。
- **因果效应的估计：**因果效应的估计可能受样本量、测量误差和模型假设的影响。
- **外部有效性：**因果推断结果可能无法推广到其他人群或环境。
- **伦理限制：**某些因果推断方法涉及对参与者的干预，这可能受到伦理限制。