基因表达数据可视化：ggplot2在生物信息学中的应用

# 1. 基因表达数据可视化概述

在生物信息学研究中，可视化是理解复杂数据的关键。基因表达数据通常包含成千上万个基因的信息，因此，有效地将这些数据可视化能够帮助研究人员快速识别模式、异常值和潜在的生物学意义。本章将介绍基因表达数据可视化的基础概念，包括可视化的重要性、常用工具，以及如何根据研究目的选择合适的可视化方法。我们将探讨数据可视化的几个核心原则，例如选择正确的图形类型、颜色和布局，以及如何通过视觉提示传达数据的关键特性。此外，本章还会提供一些实践指南，帮助读者了解如何应用这些原理到基因表达数据中，为进一步深入学习ggplot2和其他可视化工具打下坚实的基础。

# 2. ggplot2的基础知识

## 2.1 ggplot2的基本概念和安装
ggplot2是一个基于R语言的数据可视化包，它使用了一种被称为“图形语法”的绘图理念。ggplot2的核心是通过图层叠加的方式构建图形，这让用户可以灵活地创建各种复杂的统计图形。

要开始使用ggplot2，首先需要在R环境中安装它。可以通过CRAN（Comprehensive R Archive Network）的安装命令来完成：

install.packages("ggplot2")

安装完成后，使用以下代码来加载包：

library(ggplot2)

## 2.2 ggplot2的绘图原理和组件
### 2.2.1 图层概念
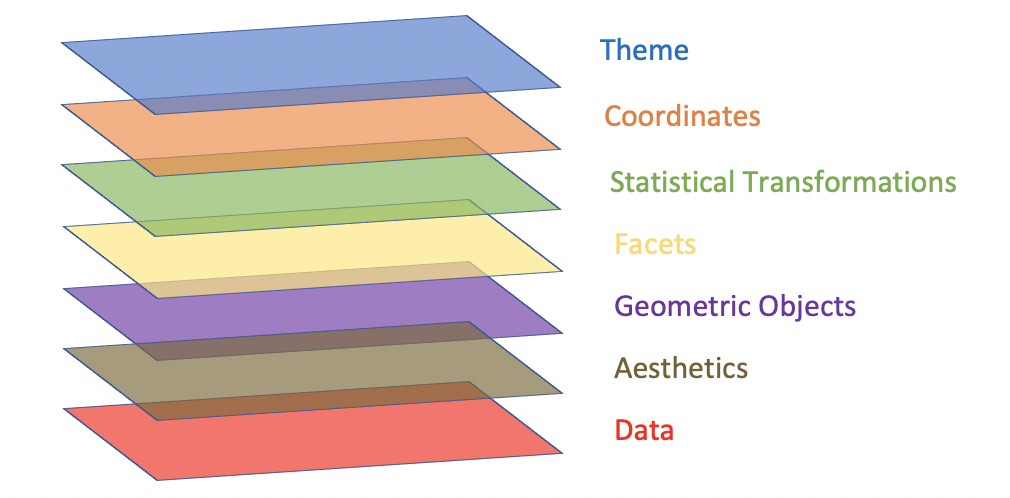
ggplot2的基本绘图单位是图层（Layer）。一个ggplot图形由多个图层组成，包括数据层、几何层、比例尺层、坐标系层和主题层。每个图层都对最终图形有特定的贡献。

例如，一个基本的散点图可以通过添加一个点几何层来创建：

ggplot(data = iris, aes(x = Sepal.Length, y = Petal.Length)) +
  geom_point()

这里`ggplot`函数创建了一个基本的图层，并通过`+`符号添加几何对象。

### 2.2.2 几何对象（Geoms）
几何对象（简称为geoms）定义了数据如何在图形中表示。例如`geom_point`用于绘制点，`geom_line`用于绘制线条，`geom_bar`用于绘制柱状图等。用户可以通过选择不同的geoms来创建多种类型的图表。

### 2.2.3 调度器（Scales）
调度器定义了数据空间到图形空间的转换规则。ggplot2默认的调度器会自动选择适合数据的尺度，但用户也可以通过指定调度器来自定义颜色、大小、形状等。

例如，自定义x轴和y轴的范围：

ggplot(data = iris, aes(x = Sepal.Length, y = Petal.Length)) +
  geom_point() +
  scale_x_continuous(limits = c(4, 8)) +
  scale_y_continuous(limits = c(1, 7))

### 2.2.4 主题（Themes）
主题控制了图形的非数据元素，例如背景颜色、网格线和字体样式。ggplot2提供了多种预设主题，用户也可以创建自定义主题以满足特定的美学需求。

例如，使用预设的主题`theme_minimal`：

ggplot(data = iris, aes(x = Sepal.Length, y = Petal.Length)) +
  geom_point() +
  theme_minimal()

## 2.3 ggplot2的数据类型和结构
### 2.3.1 数据框（Data Frames）
ggplot2绘图依赖于数据框（data frames），这是一种二维表格数据结构。每个变量是一列，每个观测是行。ggplot2对数据框中的数据类型也很敏感，不同的数据类型（如数值型、因子型、日期型）会影响绘图的方式。

### 2.3.2 长格式和宽格式数据
数据在ggplot2中的组织形式称为“格式”（format）。长格式数据（long format）易于ggplot2处理，因为它将每个观测及其变量封装在一个单元格中。宽格式数据（wide format）则将每个观测的不同变量分散在多个列中，可能需要转换才能用于绘图。

例如，将宽格式数据转换为长格式：

long_data <- reshape2::melt(wide_data)

### 2.3.3 数据清洗与转换技巧
在ggplot2中，常常需要对数据进行预处理才能进行有效的绘图。dplyr包提供了一系列的数据操作函数，如筛选、排序、分组、汇总等，是数据清洗和转换的利器。

使用dplyr进行数据分组和汇总：

library(dplyr)
grouped_data <- iris %>%
  group_by(Species) %>%
  summarise(mean_length = mean(Sepal.Length))

总结第二章的内容，ggplot2的灵活图层系统、几何对象、调度器和主题组件共同构成了其强大的数据可视化框架。通过使用R语言的数据框、长宽格式数据的转换以及数据清洗和转换技巧，ggplot2能够实现复杂的数据图形化展示。这些基础知识构成了ggplot2应用和扩展的基础，为我们深入学习和使用ggplot2打下了坚实的基础。

# 3. ggplot2的基本绘图技巧

在前一章中，我们已经探讨了ggplot2的基础知识，以及它在数据可视化中的基本原理和组件。本章将深入介绍ggplot2的基本绘图技巧，涵盖创建基本图形、图形的美化和定制，以及多个图形的组合和比较。

## 3.1 创建基本图形

ggplot2提供了一种非常直观的方式来创建基础图形，包括散点图、折线图、柱状图、箱形图等。

### 3.1.1 散点图的绘制

散点图是数据可视化中最基础且广泛使用的图形之一。它可以展示两个变量间的相互关系。

library(ggplot2)
# 加载数据集
data(mtcars)

# 绘制散点图
ggplot(data = mtcars, aes(x = wt, y = mpg)) +
    geom_point()

在这段代码中，我们使用了`geom_point()`来创建散点图。参数`aes(x = wt, y = mpg)`定义了x轴和y轴所对应的变量。`ggplot()`函数则是ggplot2包中创建图形的基础函数，它接受数据集和映射作为其基本参数。

### 3.1.2 折线图的绘制

折线图通常用来展示数据随时间或顺序的变化趋势。

# 假设我们有一个时间序列数据
time_series <- data.frame(
  time = 1:10,
  value = c(2, 3, 3.2, 3.5, 4.5, 5.3, 5.5, 6, 7, 8)
)

ggplot(time_series, aes(x = time, y = value)) +
    geom_line()

在这段代码中，`geom_line()`函数被用来绘制折线图，它将根据提供的时间序列数据将点连接成线。

### 3.1.3 柱状图和箱形图的绘制

柱状图非常适合比较不同类别的数据，而箱形图能提供有关数据分布的信息。

# 柱状图示例
ggplot(mtcars, aes(x = factor(cyl), y = mpg)) +
    geom_bar(stat = "summary", fun = "mean")

# 箱形图示例
ggplot(mtcars, aes(x = factor(cyl), y = mpg)) +
    geom_boxplot()

在这里，`geom_bar()`和`geom_boxplot()`分别用于绘制柱状图和箱形图。`stat = "summary"`和`fun = "mean"`定义了我们想要显示的是mpg的平均值。`geom_boxplot()`则直接绘制箱形图，不需要额外的统计参数。

## 3.2 图形的美化和定制

创建完基础图形之后，我们通常需要根据实际需求对图形进行美化和定制。

### 3.2.1 颜色、形状和大小的调整

调整图形元素的颜色、形状和大小可以显著提升图形的可读性和美观度。

# 设置颜色和形状
ggplot(mtcars, aes(x = wt, y = mpg, color = factor(cyl), shape = factor(gear))) +
    geom_point(size = 3)

# 设置点的大小
ggplot(mtcars, aes(x = wt, y = mpg, size = hp)) +
    geom_point()

在这段代码中，`aes(color = factor(cyl), shape = factor(gear))`和`aes(size = hp)`分别用于调整点的颜色、形状和大小。

### 3.2.2 图例和标签的定制

在图形中添加合适的图例和标签，可以帮助观众更好地理解图形所表达的信息。

# 添加标题、轴标签和图例标题
ggplot(mtcars, aes(x = wt, y = mpg, color = factor(cyl))) +
    geom_point() +
    labs(title = "MPG vs. Weight", x = "Weight", y = "Miles/(US) gallon", color = "Cylinders") +
    theme_minimal()

`labs()`函数用于定义图形的标题、轴标签和图例标题等。`theme_minimal()`函数则提供了简洁的图形主题。

### 3.2.3 坐标轴和图例的调整

有时需要调整坐标轴的范围和刻度，或者重新定位图例。

# 调整坐标轴的范围
ggplot(mtcars, aes(x = wt, y = mpg)) +
    geom_point() +