ggplot2与数据挖掘：探索性数据分析的视觉艺术

# 1. ggplot2与数据挖掘概述

数据分析与可视化的结合是现代数据科学不可或缺的一环。ggplot2是R语言中用于数据可视化的强大工具包，它基于“图形语法”理论，将复杂的数据可视化任务简化为几个简单的构建块。ggplot2不仅能够快速创建静态图表，而且能够生成具有高度可定制性的图形。它广泛应用于数据挖掘的各个阶段，从数据探索到结果解释，ggplot2都扮演着至关重要的角色。此外，ggplot2与数据挖掘技术的结合，为模型的结果可视化提供了一种强大而优雅的方式，增强了数据分析的洞察力和交互性。在本章中，我们将从ggplot2的基本概念和数据挖掘概述出发，为读者构建一个坚实的理解基础。

# 2. ggplot2基本使用技巧

## 2.1 ggplot2图形语法基础
### 2.1.1 图形对象的构建
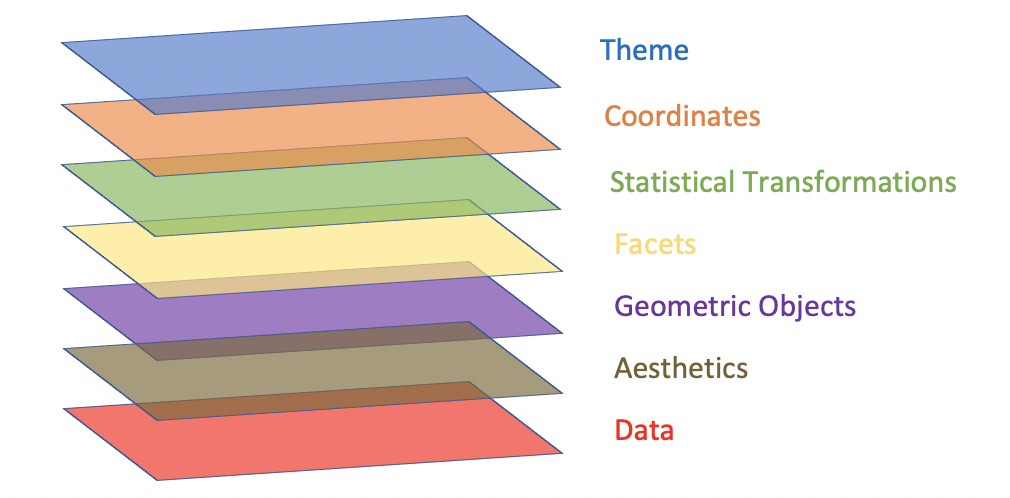
ggplot2图形对象的构建基于其特有的图形语法，首先需要加载ggplot2库并准备数据。在ggplot2中，一幅图由数据、映射、几何对象、统计变换、比例尺、坐标系统、图层和面板等要素组成。

library(ggplot2)

# 示例数据
data("mtcars")
# 创建图形对象
p <- ggplot(data = mtcars, aes(x = mpg, y = wt)) +
  geom_point() # 添加点图层
print(p)

上述代码创建了一个基础的点图，将`mtcars`数据集中的`mpg`（每加仑英里数）与`wt`（车重）的关系展示出来。这里`aes()`函数定义了数据到图形属性的映射关系，`geom_point()`则指定使用点图层来表现这些数据点。ggplot2中的图形对象是通过添加各种图层来构建的，这些图层可以包括点、线、矩形、文本等几何对象（geoms）。

### 2.1.2 图层的添加与管理
ggplot2中的图层可以通过`+`符号添加。它提供了多种图层，比如`geom_line()`用于绘制线图，`geom_histogram()`用于绘制直方图等。

# 添加线图层
p + geom_line(aes(group = 1), color = "red")

在这个例子中，我们在点图的基础上添加了一条红色的线，表示数据点的某种趋势。图层可以叠加，`ggplot`函数创建了一个图层，而`geom_line`则创建了另一个图层，通过`+`连接。每个图层可以有自己的一套美学映射。

## 2.2 数据可视化的基本元素
### 2.2.1 几何对象（geoms）
几何对象（geoms）是ggplot2中非常核心的概念。它们决定了数据如何在图形上展示。常见的geoms包括点、线、条形图、盒型图等。

# 使用不同的geoms展示数据
p <- ggplot(mtcars, aes(x = factor(cyl), y = mpg)) +
  geom_boxplot() +
  geom_jitter(width = 0.2) # 添加散点图层以显示数据点
print(p)

该代码段创建了一个箱型图，并在其上叠加了散点图层，以便在展示数据分布的同时显示各个数据点。通过调整`geom_jitter`中的`width`参数可以控制散点的分布密度和范围。

### 2.2.2 坐标系统（coordinates）
ggplot2提供了多种坐标系统，如笛卡尔坐标系、极坐标系等。坐标系的改变会影响图形中元素的展示方式，如位置、角度和长度等。

# 使用极坐标系
p + coord_polar(theta = "y")

这里通过`coord_polar`函数将基础图形转换为极坐标系下的雷达图或环形图。这种转换常用于展示比例关系，比如饼图和环形图等。在极坐标系中，角度成为关键维度。

### 2.2.3 标度与映射（scales）
标度（scales）控制了数据到图形属性的映射方式，比如数据的范围对应图形的长度、颜色、大小等。

p + scale_y_continuous(breaks = seq(0, 40, by = 5))

在这个例子中，通过`scale_y_continuous`函数调整了y轴的刻度，使其每5个单位一个间隔。标度函数可以用于控制颜色、形状、尺寸等多种图形属性的映射方式。

## 2.3 ggplot2的颜色和主题
### 2.3.1 颜色的美学应用
在ggplot2中，颜色是一个重要的视觉属性，可以用来表示数据的分类或者区分不同的数据点。

# 使用颜色映射
p <- ggplot(mtcars, aes(x = wt, y = mpg, color = factor(cyl))) +
  geom_point()
print(p)

这段代码通过颜色区分了不同缸数的汽车数据点，颜色的美学应用增强了图形的信息表达能力。使用`aes()`函数内的`color`参数，可以将颜色属性映射到某个因子或连续变量上。

### 2.3.2 主题的自定义与应用
ggplot2提供了一系列预设的图形主题，用于调整非数据图形属性的外观，如背景颜色、网格线、文本字体等。

p + theme_minimal() + labs(title = "Minimalist Theme")

这里通过`theme_minimal`函数应用了一个简洁的图形主题，并通过`labs`函数添加了标题。主题的自定义可以完全控制图形的外观，也可以通过`theme`函数对图形的各个细节进行精细调整。

通过上述内容的展开，我们由浅入深地学习了ggplot2的基本使用技巧，为后续更深入的数据可视化和探索性数据分析打下了坚实的基础。

# 3. ggplot2在探索性数据分析中的应用

在数据科学的实践中，探索性数据分析（EDA）是不可或缺的一个步骤。它帮助分析师理解数据的结构、发现数据之间的关系，并且识别异常值或错误。ggplot2作为R语言中最流行的可视化工具之一，非常适合用于EDA。ggplot2提供了一系列功能强大的图形对象，让数据探索变得直观和高效。

## 3.1 数据分布的可视化

### 3.1.1 直方图与密度图

在探索性数据分析中，直方图是一种直观地展现数据分布的图表。直方图将数据分割成一系列连续的区间（通常称为“bins”），每个区间内数据点的数量通过矩形的面积来表示。这使得我们能够判断数据的分布类型、识别异常值和发现数据的聚集趋势。

ggplot2可以通过简单的指令来创建直方图。下面的代码展示了如何使用ggplot2创建直方图，并对直方图进行个性化调整：

# 加载ggplot2包
library(ggplot2)

# 生成一些模拟数据
set.seed(123)
data <- data.frame(values = rnorm(100))

# 创建直方图
ggplot(data, aes(x = values)) + 
  geom_histogram(bins = 30, fill = "blue", color = "black") +
  labs(title = "直方图示例", x = "值", y = "频数") +
  theme_minimal()

### 3.1.2 散点图与箱型图

散点图是探索两个连续变量之间关系的常用方式。通过散点图，我们可以观察变量间