医学成像中的对数坐标：5个应用案例，可视化细胞分布和病变区域

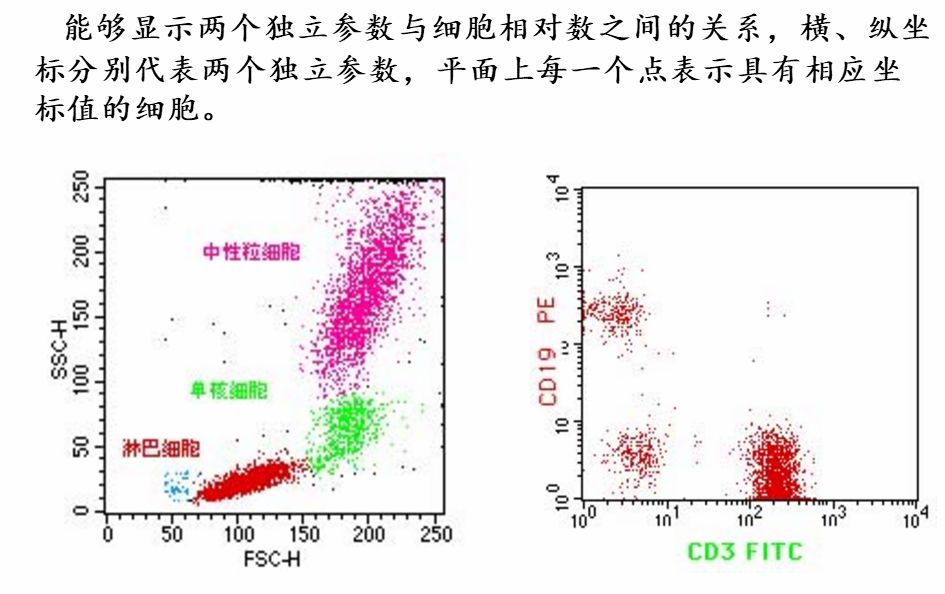
# 1. 对数坐标在医学成像中的概述**

对数坐标是一种非线性坐标系统，它将数据值转换为其对数。在医学成像中，对数坐标用于表示具有宽动态范围的数据，例如细胞分布、病变大小和信号强度。

通过使用对数坐标，医学图像可以更有效地显示数据，突出感兴趣的特征。对数变换可以将广泛分布的数据压缩到较窄的范围内，从而提高图像的对比度和可视化效果。此外，对数坐标还可以揭示数据中的模式和趋势，这对于医学诊断和研究至关重要。

# 2. 对数坐标的理论基础

### 2.1 数据分布和对数变换

在医学成像中，数据通常呈现出非正态分布，即数据分布不均匀，存在大量极端值。例如，细胞大小和分布的数据可能存在大量小细胞和少数大细胞。这种非正态分布会影响数据的可视化和分析。

对数变换是一种数学变换，可以将非正态分布的数据转换为更接近正态分布。对数变换的公式为：

y = log10(x)

其中：

* x 是原始数据
* y 是对数变换后的数据

对数变换通过压缩大值和拉伸小值，使数据分布更接近正态分布。这使得数据可视化和分析更加容易。

### 2.2 对数坐标的优势和局限性

**优势：**

* **提高数据可视化：**对数坐标可以将非正态分布的数据转换为更接近正态分布，从而提高数据的可视化效果。这使得识别数据中的模式和趋势更加容易。
* **增强对比度：**对数坐标可以增强数据中的对比度，使小值和极值更加明显。这对于识别和分析微小变化非常有用。
* **简化数据分析：**对数坐标可以简化数据分析，因为对数变换后的数据更接近正态分布，符合许多统计模型的假设。

**局限性：**

* **数据失真：**对数变换可能会导致数据失真，因为对数变换会改变数据的原始值。这可能会影响某些分析，例如计算平均值和标准差。
* **负值处理：**对数坐标无法处理负值数据。因此，在处理包含负值的医学图像数据时，需要考虑其他方法。
* **解释困难：**对数坐标的数据解释可能比原始数据更困难，因为对数坐标中的值与原始数据中的值并不直接对应。

# 3. 对数坐标在医学成像中的实践应用**

### 3.1 细胞分布的可视化

#### 3.1.1 细胞大小和分布的分析

对数坐标可以有效地揭示细胞大小和分布的差异。通过将细胞大小数据转换为对数坐标，可以将分布范围缩小，从而增强小细胞和大型细胞之间的对比度。这对于识别细胞异质性和异常细胞至关重要。

import numpy as np
import matplotlib.pyplot as plt

# 生成模拟细胞大小数据
cell_sizes = np.random.lognormal(mean=3, sigma=0.5, size=1000)

# 绘制直方图
plt.hist(cell_sizes, bins=50)
plt.xlabel("Cell Size")
plt.ylabel("Frequency")
plt.show()

# 绘制对数坐标直方图
plt.hist(cell_sizes, bins=50, log=True)
plt.xlabel("Cell Size (Log Scale)")
plt.ylabel("Frequency")
plt.show()

**代码逻辑分析：**

* `np.random.lognormal()` 函数生成服从对数正态分布的随机数据，该分布通常用于模拟细胞大小等生物学数据。
* `plt.hist()` 函数绘制直方图，显示数据分布。
* 在第二个直方图中，`log=True` 参数将 x 轴转换为对数坐标，从而缩小分布范围并增强对比度。

#### 3.1.2 细胞数量和密度评估

对数坐标还可以用于评估细胞数量和密度。通过将细胞计数转换为对数坐标，可以将大范围的计数值压缩到更易于比较的范围内。这对于检测细胞密度变化和识别异常区域非常有用。

import numpy as np
import matplotlib.pyplot as plt

# 生成模拟细胞计数数据
cell_counts = np.random.poisson(lam=10, size=1000)

# 绘制直方图
plt.hist(cell_counts, bins=50)
plt.xlabel("Cell Count")
plt.ylabel("Frequency")
plt.show()

# 绘制对数坐标直方图
plt.hist(cell_counts, bins=50, log=True)
plt.xlabel("Cell Count (Log Scale)")
plt.ylabel("Frequency")
plt.show()

**代码逻辑分析：**

* `np.r