MATLAB仿真建模详解：揭秘仿真建模的原理与实战应用

# 1. 仿真建模概述**

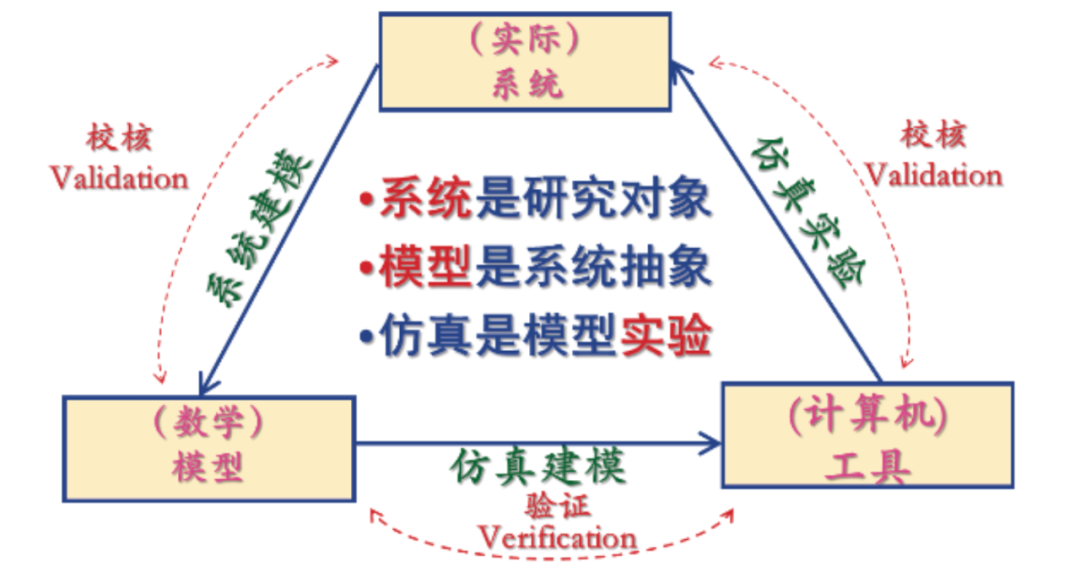
仿真建模是一种利用计算机模拟真实世界系统或过程的技术。它通过建立数学模型来描述系统的行为，然后使用计算机来求解这些模型，从而预测系统的输出。仿真建模广泛应用于工程、科学和商业等领域，用于设计、优化和分析系统。

MATLAB是一种强大的技术计算软件，它提供了广泛的工具和函数，非常适合仿真建模。MATLAB仿真建模环境提供了直观的图形用户界面和强大的编程语言，使工程师和科学家能够轻松地创建和求解仿真模型。

# 2. MATLAB仿真建模基础

### 2.1 MATLAB仿真建模环境介绍

#### 2.1.1 MATLAB仿真建模工具箱

MATLAB提供了丰富的仿真建模工具箱，包括：

- **Simulink：**图形化仿真环境，用于构建和模拟动态系统模型。
- **Control System Toolbox：**用于控制系统分析和设计的工具箱。
- **Optimization Toolbox：**用于优化问题的求解。
- **Signal Processing Toolbox：**用于信号处理和分析。

#### 2.1.2 MATLAB仿真建模流程

MATLAB仿真建模流程通常包括以下步骤：

1. **建立模型：**使用Simulink或其他工具创建系统模型。
2. **参数设置：**设置模型参数，包括初始条件、输入信号和仿真时间。
3. **仿真运行：**运行仿真，生成系统响应数据。
4. **结果分析：**分析仿真结果，评估系统性能。

### 2.2 MATLAB仿真建模语言

MATLAB仿真建模语言基于MATLAB语言，并扩展了用于仿真建模的特定函数和语法。

#### 2.2.1 MATLAB仿真建模语法

MATLAB仿真建模语法遵循以下规则：

- **模型定义：**使用`sim`函数定义仿真模型。
- **参数设置：**使用`set_param`函数设置模型参数。
- **仿真运行：**使用`sim`函数运行仿真。
- **结果获取：**使用`get_param`函数获取仿真结果。

#### 2.2.2 MATLAB仿真建模函数

MATLAB仿真建模提供了丰富的函数，包括：

- **`sim`：**运行仿真。
- **`set_param`：**设置模型参数。
- **`get_param`：**获取仿真结果。
- **`simulink`：**打开Simulink环境。
- **`add_block`：**向Simulink模型添加模块。

% 定义仿真模型
sim_model = sim('model_name');

% 设置模型参数
set_param(sim_model, 'StopTime', '10');

% 运行仿真
sim(sim_model);

% 获取仿真结果
仿真结果 = get_param(sim_model, 'yout');

**逻辑分析：**

1. `sim`函数定义了仿真模型，指定了模型名称。
2. `set_param`函数设置了模型的停止时间为10秒。
3. `sim`函数运行仿真。
4. `get_param`函数获取了模型的输出数据。

# 3. MATLAB仿真建模实践

### 3.1 连续系统仿真

#### 3.1.1 微分方程建模

连续系统仿真涉及使用微分方程来描述系统的行为。微分方程是一阶或更高阶的方程，其中一个或多个变量及其导数相对于时间。对于连续系统，状态变量的导数由微分方程定义。

例如，考虑一个简单的弹簧质量阻尼系统。该系统的运动可以用以下微分方程描述：

m * d^2x/dt^2 + c * dx/dt + k * x = F(t)

其中：

* `m` 是质量
* `c` 是阻尼系数
* `k` 是弹簧常数
* `x` 是位移
* `F(t)` 是外力

#### 3.1.2 MATLAB仿真实现

MATLAB提供了一系列函数来求解微分方程，包括`ode45`和`ode23s`。这些函数使用数值方法来近似求解微分方程。

以下MATLAB代码展示了如何使用`ode45`求解弹簧质量阻尼系统的微分方程：

% 定义系统参数
m = 1; % 质量
c = 0.1; % 阻尼系数
k = 10; % 弹簧常数

% 定义外力
F = @(t) 0; % 没有外力

% 定义微分方程
ode = @(t, x) [x(2); (-c/m) * x(2) - (k/m) * x(1) + F(t)/m];

% 定义初始条件
x0 = [0; 0]; % 初始位移和速度为 0

% 求解微分方程
[t, x] = ode45(ode, [0, 10], x0);

% 绘制结果
plot(t, x(:, 1));
xlabel('时间 (s)');
ylabel('位移 (m)');

### 3.2 离散系统仿真

#### 3.2.1 差分方程建模

离散系统仿真涉及使用差分方程来描述系统的行为。差分方程是一阶或更高阶的方程，其中一个或多个变量及其差分相对于时间。对于离散系统，状态变量的差分由差分方程定义。

例如，考虑一个简单的数字滤波器。该滤波器的输出可以通过以下差分方程描述：

y[n] = a * y[n-1] + b * x[n]

其中：

* `y[n]` 是输出信号
* `x[n]` 是输入信号
* `a` 和 `b` 是滤波器系数

#### 3.2.2 MATLAB仿真实现

MATLAB提供了`filter`函数来实现离散系统仿真。该函数使用差分方程来计算离散系统的输出。

以下MATLAB代码展示了如何使用`filter`函数实现数字滤波器：

% 定义滤波器系数
a = 0.9;
b = 0.1;

% 定义输入信号
x = randn(100, 1);

% 应用滤波器
y = filter(b, a, x);

% 绘制结果
plot(x);
hold on;
plot(y, 'r');
xlabel('样本');
ylabel('幅度');
legend('输入信号', '输出信号');

# 4. MATLAB仿真建模高级应用

### 4.1 优化算法集成

#### 4.1.1 遗传算法

遗传算法是一种受自然界生物进化启发的优化算法，它通过模拟生物进化过程中的选择、交叉和变异等机制，不断迭代优化目标函数。在MATLAB中，可以使用Genetic