Cumsum函数的终极指南：掌握数据分析中的趋势分析利器

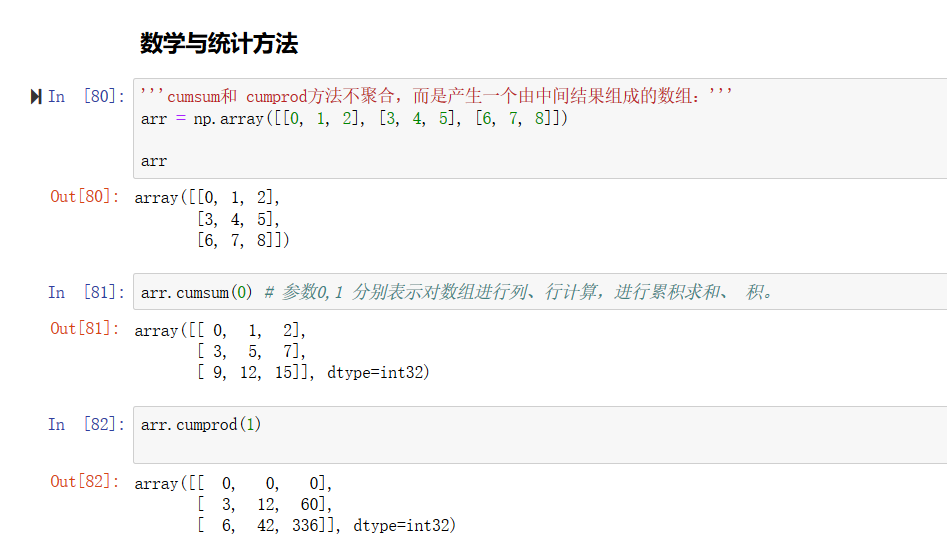
# 1. Cumsum函数的简介和基本原理**

Cumsum函数是一种累积和函数，用于计算序列中每个元素的累积和。它在数据分析中广泛应用，特别是在趋势分析和异常检测方面。

**基本原理：**

Cumsum函数通过迭代计算序列中的每个元素的累积和来工作。对于序列[x1, x2, ..., xn]，Cumsum函数的输出序列[y1, y2, ..., yn]如下：

y1 = x1
y2 = x1 + x2
yn = x1 + x2 + ... + xn

通过这种方式，Cumsum函数可以揭示序列中的累积趋势和模式，从而为数据分析提供有价值的见解。

# 2. Cumsum函数的应用场景和实战案例

### 2.1 趋势分析与异常检测

#### 2.1.1 识别数据中的上升或下降趋势

Cumsum函数可以用来识别数据中的上升或下降趋势。具体操作如下：

1. 计算数据的累积和序列。
2. 从累积和序列中减去其移动平均。
3. 绘制所得序列的折线图。

如果折线图显示出上升趋势，则表明数据中存在上升趋势；如果折线图显示出下降趋势，则表明数据中存在下降趋势。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 生成模拟数据
data = np.random.randn(100)

# 计算累积和序列
cumsum_data = np.cumsum(data)

# 计算移动平均
window_size = 10
moving_average = pd.Series(data).rolling(window_size).mean()

# 绘制折线图
plt.plot(cumsum_data - moving_average)
plt.show()

**逻辑分析：**

* `np.cumsum(data)`：计算数据的累积和序列。
* `pd.Series(data).rolling(window_size).mean()`：计算数据的移动平均，窗口大小为 `window_size`。
* `cumsum_data - moving_average`：从累积和序列中减去移动平均。

#### 2.1.2 检测数据中的异常值和异常模式

Cumsum函数还可以用来检测数据中的异常值和异常模式。具体操作如下：

1. 计算数据的累积和序列。
2. 计算累积和序列的移动平均。
3. 计算累积和序列与移动平均之间的差值。
4. 绘制差值序列的折线图。

如果折线图显示出尖峰或谷值，则表明数据中存在异常值或异常模式。

# 计算差值序列
diff_series = cumsum_data - moving_average

# 绘制折线图
plt.plot(diff_series)
plt.show()

**逻辑分析：**

* `diff_series = cumsum_data - moving_average`：计算累积和序列与移动平均之间的差值。

### 2.2 累积和计算

#### 2.2.1 计算数据的累积和

Cumsum函数可以用来计算数据的累积和。具体操作如下：

# 计算数据的累积和
cumsum_data = np.cumsum(data)

**参数说明：**

* `data`：要计算累积和的一维数组。

#### 2.2.2 计算数据中的移动平均

Cumsum函数还可以用来计算数据中的移动平均。具体操作如下：

# 计算数据的移动平均
moving_average = pd.Series(data).rolling(window_size).mean()

**参数说明：**

* `data`：要计算移动平均的一维数组。
* `window_size`：移动平均的窗口大小。

# 3.1 窗口大小和步长的选择

#### 3.1.1 窗口大小对结果的影响

窗口大小是Cumsum函数中一个关键参数，它决定了累积和计算中包含的数据点的数量。窗口大小的选择会对结果产生显著影响：

- **较小的窗口大小：**可以更快速地检测到数据中的变化，但也会导致结果更加敏感，容易受到噪声和异常值的影响。
- **较大的窗口大小：**可以平滑数据中的波动，减少噪声的影响，但也会降低对变化的灵敏度，可能导致检测延迟。

因此，在选择窗口大小时，需要考虑数据的特性和分析目标。对于噪声较小、变化频繁的数据，较小的窗口大小可能更合适；对于噪声较大、变化缓慢的数据，较大的窗口大小可能更合适。

#### 3.1.2 步长对结果的灵敏度

步长是Cumsum函数中另一个重要参数，它决定了累积和计算中数据点之间的移动间隔。步长的选择也会影响结果的灵敏度：

- **较小的步长：**可以更精确地跟踪数据中的变化，但也会增加计算量。
- **较大的步长：**可以减少计算量，但可能会导致对变化的检测延迟。

因此，在选择步长时，需要考虑数据的变化频率和分析需求。对于变化频繁的数据，较小的步长可能更合适；对于变化缓慢的数据，较大的步长可能更合适。

### 3.2 Cumsum函数的并行化和加速

#### 3.2.1 利用多核处理器提升计算效率

Cumsum函数的计算过程可以并行化，以利用多核处理器的优势。通过将数据分成多个块，并使用多线程同时处理这些块，可以显著提高计算效率。

#### 3.2.2 使用分布式计算框架进行并行化

对于海量数据，使用分布式计算框架（如Apache Spark）可以进一步并行化Cumsum函数的计算。分布式计算框架可以将数据分布到多个节点上，并行执行计算任务，从而大幅缩短计算时间。

**代码示例：**

import numpy as np
from dask import dataframe as dd

# 创建一个分布式DataFrame
df = dd.from_pandas(pd.DataFrame({'data': np.random.randn(1000000)}))

# 使用分布式计算框架并行化Cumsum计算
cumsum = df['data'].cumsum()

# 计算结果
result = cumsum.compute()

**逻辑分析：**

此代码示例使用Dask分布式计算框架并行化了Cumsum函数的计算。首先，将数据加载到分布式DataFrame中。然后，使用`cumsum()`方法计算累积和。最后，使用`compute()`方法触发并行计算并获取结果。

# 4. Cumsum函数在数据分析中的实战应用

Cumsum函数在数据分析领域有着广泛的应用，特别是在时间序列分析中。本章将介绍Cumsum函数在金融时间序列分析和医疗保健数据分析中的具体应用场景，并通过实战案例展示其强大的分析能力。

### 4.1 金融时间序列分析

#### 4.1.1 股票价格趋势预测

股票价格趋势预测是金融领域的重要课题。Cumsum函数可以用来识别股票价格的上升或下降趋势，为投资者提供决策依据。

**案例：**

假设我们有一组历史股票价格数据，如下所示：

import pandas as pd

data = pd.read_csv('stock_prices.csv')
data['Date'] = pd.to_datetime(data['Date'])
data.set_index('Date', inplace=True)

我们可以使用Cumsum函数计算股票价格的累积和，并绘制出累积和曲线：

data['cumsum'] = data['Close'].cumsum()
data['cumsum'].plot()

从累积和曲线上，我们可以观察到股票价格的整体趋势。上升趋势表现为累积和曲线向上倾斜，而下降趋势则表现为累积和曲线向下倾斜。

#### 4.1.2 外汇汇率波动分析

外汇汇率波动分析是另一个重要的金融应用场景。Cumsum函数可以用来检测外汇汇率的异常波动，帮助交易者识别潜在的交易机会。

**案例：**

假设我们有一组历史外汇汇率数据，如下所示：

import pandas as pd

data = pd.read_csv('forex_rates.csv')
data['Date'] = pd.to_datetime(data['Date'])
data.set_index('Date', inplace=True)

我们可以使用Cumsum函数计算外汇汇率的累积和，并绘制出累积和曲线：

data['cumsum'] = data['Rate'].cumsum()
data['cumsum'].plot()

从累积和曲线上，我们可以观察到外汇汇率的波动情况。剧烈的波动表现为累积和曲线的急剧上升或下降，而平稳的波动则表现为累积和曲线的平缓变化。

### 4.2 医疗保健数据分析

#### 4.2.1 疾病发病率趋势监测

疾病发病率趋势监测是医疗保健领域的重要任务。Cumsum函数可以用来识别疾病发病率的上升或下降趋势，帮助卫生部门及时采取干预措施。

**案例：**

假设我们有一组历史疾病发病率数据，如下所示：

import pandas as pd

data = pd.read_csv('disease_incidence.csv')
data['Date'] = pd.to_datetime(data['Date'])
data.set_index('Date', inplace=True)

我们可以使用Cumsum函数计算疾病发病率的累积和，并绘制出累积和曲线：

data['cumsum'] = data['Incidence'].cumsum()
data['cumsum'].plot()

从累积和曲线上，我们可以观察到疾病发病率的整体趋势。上升趋势表现为累积和曲线向上倾斜，而下降趋势则表现为累积和曲线向下倾斜。

#### 4.2.2 药物疗效评估

药物疗效评估是医疗保健领域另一个重要的应用场景。Cumsum函数可以用来检测药物治疗效果的显著性，帮助医生评估药物的有效性。

**案例：**

假设我们有一组药物治疗前后患者的健康指标数据，如下所示：

import pandas as pd

data = pd.read_csv('drug_efficacy.csv')
data['Date'] = pd.to_datetime(data['Date'])
data.set_index('Date', inplace=True)

我们可以使用Cumsum函数计算患者健康指标的累积和，并绘制出累积和曲线：

data['cumsum'] = data['Health Indicator'].cumsum()
data['cumsum'].plot()

从累积和曲线上，我们可以观察到患者健康指标的变化情况。显著的改善表现为累积和曲线向上倾斜，而显著的恶化则表现为累积和曲线向下倾斜。

# 5. Cumsum函数的局限性和替代方案

### 5.1 Cumsum函数的局限性

尽管Cumsum函数是一个强大的工具，但它也有一些局限性：

- **对噪声数据的敏感性：**Cumsum函数对噪声数据非常敏感，这可能会导致错误的趋势或异常检测结果。
- **无法处理季节性数据：**Cumsum函数无法处理具有季节性模式的数据，这可能会导致误导性的结果。

### 5.2 Cumsum函数的替代方案

在某些情况下，其他函数可能是Cumsum函数的更好的替代方案：

- **滑动平均：**滑动平均通过计算一定时间窗口内数据的平均值来平滑数据。它可以减少噪声的影响，但可能会滞后于实际趋势。
- **指数加权移动平均（EWMA）：**EWMA通过赋予最近数据更高的权重来计算移动平均。它比滑动平均更灵敏，可以更快地响应趋势变化。

**代码示例：**

import numpy as np
import pandas as pd

# 创建一个带有噪声数据的序列
data = np.random.randn(100) + 50

# 计算Cumsum
cumsum = np.cumsum(data)

# 计算滑动平均
window_size = 10
rolling_mean = pd.Series(data).rolling(window_size).mean()

# 计算EWMA
alpha = 0.5
ewma = pd.Series(data).ewm(alpha=alpha).mean()

**表格比较：**

| 函数 | 优点 | 缺点 |
|---|---|---|
| Cumsum | 识别趋势和异常值 | 对噪声数据敏感，无法处理季节性数据 |
| 滑动平均 | 平滑数据，减少噪声 | 可能滞后于实际趋势 |
| EWMA | 灵敏，快速响应趋势变化 | 可能对异常值过于敏感 |