MATLAB欧拉法与Runge-Kutta法：数值解方法深入对比

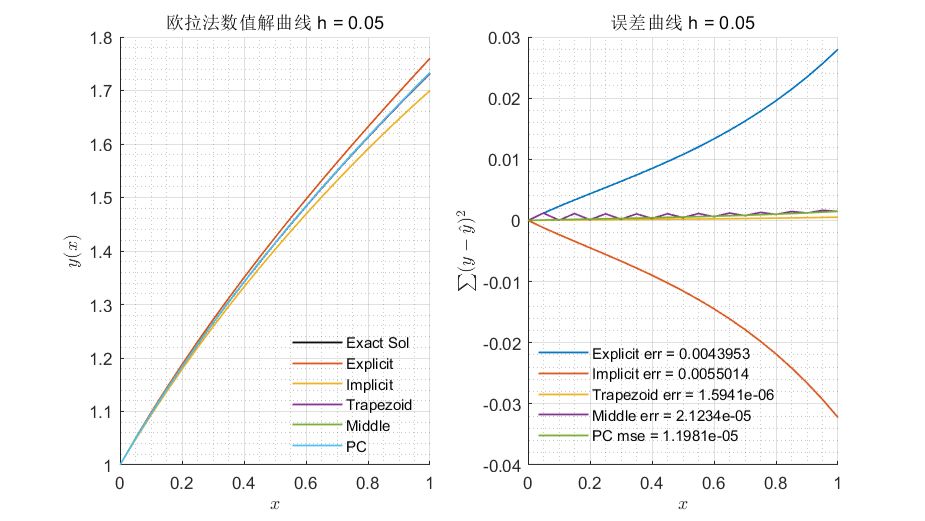
# 1. 数值解方法概述

数值解方法是求解微分方程近似解的一种有效方法，它将微分方程转化为一系列代数方程，通过迭代计算得到微分方程的近似解。数值解方法的优点是计算简单，易于实现，适用于求解各种类型的微分方程。

数值解方法主要分为两类：显式方法和隐式方法。显式方法直接利用微分方程的导数来计算近似解，计算简单，但稳定性较差；隐式方法利用微分方程的导数和近似解来计算近似解，计算复杂，但稳定性较好。

# 2. 欧拉法

### 2.1 欧拉法的基本原理

欧拉法是一种一阶显式数值解法，用于求解常微分方程。其基本原理是：

给定常微分方程：

y' = f(x, y)

其中：

* `y` 是待求解的函数
* `x` 是自变量
* `f(x, y)` 是函数 `y` 的导数

欧拉法通过以下步骤求解常微分方程：

1. 给定初始条件 `y(x_0) = y_0`
2. 对于给定的 `x_n`，计算 `y_{n+1}`：

y_{n+1} = y_n + h * f(x_n, y_n)

其中：

* `h` 是步长
* `y_n` 是 `x_n` 处的近似解
* `f(x_n, y_n)` 是 `y` 在 `x_n` 处的导数

### 2.2 欧拉法的实现步骤

欧拉法的实现步骤如下：

1. 输入常微分方程、初始条件和步长
2. 初始化 `y_0` 和 `x_0`
3. 循环计算 `y_{n+1}`，直到达到给定的 `x` 值
4. 输出近似解 `y_n`

### 2.3 欧拉法的误差分析

欧拉法是一种一阶方法，其误差为 `O(h)`。这意味着，当步长 `h` 减小时，误差会减小。欧拉法的误差分析如下：

y(x_{n+1}) - y_{n+1} = h * f(x_n, y_n) + O(h^2)

其中：

* `y(x_{n+1})` 是 `x_{n+1}` 处的精确解
* `y_{n+1}` 是欧拉法计算的近似解

从误差分析中可以看出，欧拉法在步长较小的情况下误差较小，在步长较大时误差较大。因此，在实际应用中，需要根据精度要求选择合适的步长。

**代码块：**

def euler_method(f, x0, y0, h, n):
    """
    欧拉法求解常微分方程

    参数：
        f: 常微分方程右端函数
        x0: 初始自变量值
        y0: 初始函数值
        h: 步长
        n: 迭代次数

    返回：
        x: 自变量值列表
        y: 近似解列表
    """

    x = [x0 + i * h for i in range(n + 1)]
    y = [y0]

    for i in range(n):
        y.append(y[i] + h * f(x[i], y[i]))

    return x, y

**代码逻辑分析：**

* `euler_method()` 函数接受常微分方程右端函数 `f`、初始条件 `x0`、`y0`、步长 `h` 和迭代次数 `n` 作为参数。
* 函数首先初始化自变量值列表 `x` 和近似解列表 `y`。
* 然后，函数循环迭代 `n` 次，计算每个自变量值 `x[i]` 处的近似解 `y[i]`。
* 最后，函数返回自变量值列表 `x` 和近似解列表 `y`。

**参数说明：**

* `f`: 常微分方程右端函数，接受自变量 `x` 和函数值 `y` 作为参数，返回导数值 `f(x, y)`。
* `x0`: 初始自变量值。
* `y0`: 初始函数值。
* `h`: 步长。
* `n`: 迭代次数。

# 3. Runge-Kutta法

### 3.1 Runge-Kutta法的基本原理

Runge-Kutta法是一种显式数值解法，用于求解一阶常微分方程和二阶常微分方程。与欧拉法不同，Runge-Kutta法采用多步计算，在每个步骤中使用前一步计算的结果来计算当前步的近似值。

Runge-Kutta法的基本原理是：

y_n+1 = y_n + h * f(t_n, y_n)

其中：

* `y_