提升效率的循环算法优化策略：数据结构处理的秘诀

# 1. 循环算法优化的重要性与基本原则

## 1.1 为什么要优化循环算法

循环算法是程序中最常见的结构之一，尤其在处理大量数据和执行重复任务时。优化循环算法的重要性不仅体现在提高代码效率上，还关乎整体性能的提升，资源的有效利用，以及为复杂问题的解决铺平道路。在IT行业中，一个细微的性能提升可能会导致大规模应用下的显著差异，从而影响用户体验和业务成果。

## 1.2 循环优化的基本原则

优化循环算法时，应遵循几个基本原则：

- **最小化循环内部的计算量**：尽量避免在每次迭代中重复的计算。
- **减少循环内部的内存访问**：内存访问的延迟远高于CPU的计算延迟。
- **利用局部性原理**：缓存原理暗示我们应尽可能利用局部性原理，优化数据的访问模式。
- **算法与硬件协同**：理解硬件特性，比如并行处理能力，可以让我们更好地优化循环。

遵循这些原则，开发者可以在不同层面上对循环算法进行优化，从而显著提升程序的运行效率。在后续章节中，我们将深入探讨循环结构的优化方法、实践案例分析，以及高级策略，进一步揭示循环算法优化的广阔天地。

# 2. 循环结构的理论基础与优化方法

## 2.1 循环算法的时间复杂度分析

### 2.1.1 理解时间复杂度

时间复杂度是衡量算法运行时间与输入数据大小之间关系的指标。它帮助我们估算算法的执行时间，而与特定的机器或实现无关。在循环算法中，时间复杂度尤为重要，因为它直接关系到算法在处理大数据集时的性能表现。

循环的次数通常决定算法的时间复杂度。例如，单层循环算法的时间复杂度可能是O(n)，而嵌套循环算法的时间复杂度可能是O(n²)。在分析时间复杂度时，我们关注的是循环中每次迭代的最高次数，也就是主导项。

### 2.1.2 常见算法的时间复杂度对比

不同类型的算法在时间复杂度上有着显著的差异，如下表所示：

| 算法类型 | 时间复杂度 | 应用场景举例 |
| -------------- | ------------------ | ---------------------- |
| 线性搜索 | O(n) | 线性表查找 |
| 二分搜索 | O(log n) | 排序数组中查找 |
| 冒泡排序 | O(n²) | 小规模数据排序 |
| 快速排序 | O(n log n) | 大规模数据排序 |
| 动态规划 | O(n²), O(n³), ... | 优化问题（如背包问题） |
| 分治法 | O(n log n) | 归并排序、快速幂运算 |
| 贪心算法 | O(n log n) | Prim算法、Dijkstra算法 |

从上表可以看出，一个算法的时间复杂度可以是多种不同的形式，取决于它的具体实现和数据结构。为了优化循环算法，我们应该优先考虑降低时间复杂度，选择更有效的算法实现。

## 2.2 循环结构的代码实现技巧

### 2.2.1 循环的初始化与终止条件

循环的初始化和终止条件是确保算法正确性的基础。初始化负责设置循环开始前的状态，终止条件决定了循环何时停止。以下是一些关于循环初始化与终止条件的优化技巧：

- **初始化**：尽量减少循环内的初始化操作。如果可能，将初始化放在循环外进行，这样可以避免每次迭代都进行不必要的计算。
- **终止条件**：确保循环能够在达到逻辑结束时立即停止。避免使用复杂的终止条件表达式，这可能会使代码难以理解并且影响性能。

// 错误示例
for(int i = 0; i < array.length; i++) {
    if (array[i] > 0) {
        // 处理逻辑
    }
}

// 优化后
for(int i = 0; i < array.length; ++i) {
    if (array[i] <= 0) {
        continue; // 直接跳过剩余逻辑
    }
    // 处理逻辑
}

### 2.2.2 循环体的优化策略

优化循环体是提高算法效率的关键步骤。以下是一些循环体的优化策略：

- **减少不必要的计算**：在循环体内部避免重复计算相同的值或进行不必要的操作。
- **延迟计算**：如果可能，将计算推迟到实际需要时进行。
- **减少函数调用**：函数调用是有开销的，尤其是在循环体内部。尽量在循环外进行函数调用，或使用函数指针。

// 减少不必要的计算和函数调用
double a = 0.5; // 预先计算的常数
for(int i = 0; i < array.length; ++i) {
    array[i] *= a;
}

## 2.3 循环中的数据结构选择

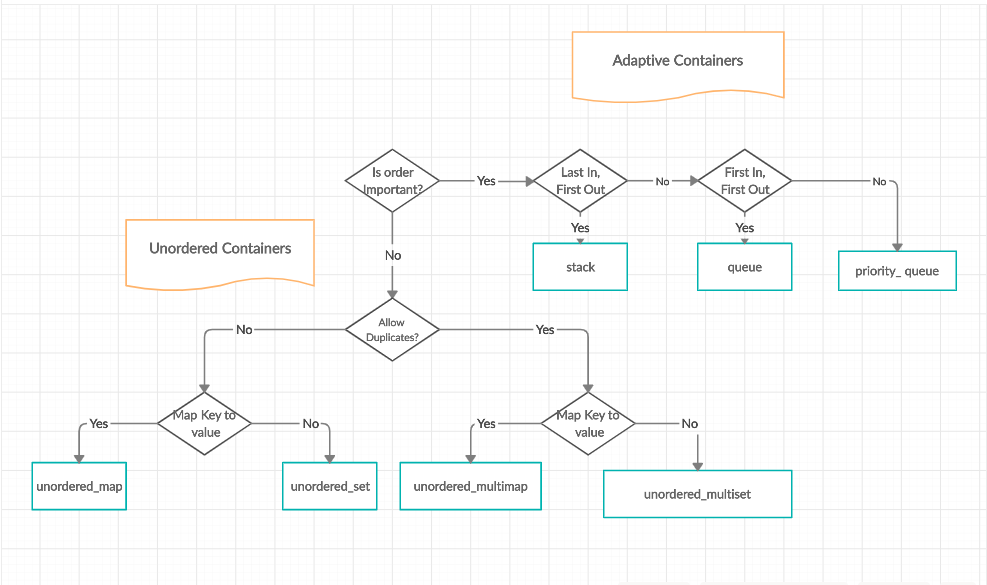
### 2.3.1 不同数据结构的适用场景

不同的数据结构有着不同的特性和使用场景，选择合适的数据结构对于循环算法的性能至关重要。下面列出了常见的数据结构及其适用场景：

- **数组**：用于存储固定大小的元素序列。
- **链表**：用于频繁插入和删除操作的场景。
- **栈和队列**：用于需要后进先出（LIFO）或先进先出（FIFO）操作的场景。
- **树（如二叉树、红黑树）**：用于需要快速查找、插入和删除的场景。
- **哈希表**：用于需要快速查找元素的场景。

### 2.3.2 数据结构与算法效率的关联

算法的效率往往受到所使用数据结构的直接影响。例如，如果一个算法需要频繁查找最小元素，使用最小堆这样的数据结构可能会得到更好的性能。下面是一个使用最小堆优化寻找数组中最小元素的例子：

#include <queue>

int findMinInArray(int array[], int size) {
    std::priority_queue<int, std::vector<int>, std::greater<int>> minHeap;
    for(int i = 0; i < size; ++i) {
        minHeap.push(array[i]);
    }
    ***();
}

在这个例子中，我们使用了优先队列（最小堆）来维护一个元素集合，并在O(1)时间内得到最小值。这种方法比简单的遍历数组更高效，尤其是在查找最小值的次数较多时。

以上内容提供了循环算法优化理论基础的全面概述，并通过具体的代码实现技巧和数据结构选择展示了如何实际应用这些理论。接下来的章节将继续深入探讨循环优化的实践案例和高级策略。

# 3. 实践案例分析：优化循环算法的策略应用

## 3.1 动态规划与循环优化

### 3.1.1 动态规划的基本概念

动态规划（Dynamic Programming，DP）是一种算法设计技巧，用于求解具有重叠子问题和最优子结构特性的问题。动态规划将复杂问题分解为较小子问题，通过解决这些子问题来构建最优解。在循环算法优化中，动态规划可以帮助减少重复计算，提高算法效率。

子问题之间通常存在两种关系：最优子结构，意味着问题的最优解包含其子问题的最优解；重叠子问题，即不同的子问题可能包含相同的更小子问题。在循环结构中应用动态规划，可以将这些重叠子问题的解存储起来，避免重复计算，即常说的“记忆化”（memoization）。

### 3.1.2 动态规划在循环优化中的应用实例

以经典的斐波那契数列为例，使用递归方法计算第n个斐波那契数的效率很低，因为它包含了大量的重复计算。通过引入动态规划和循环，我们可以显著提高计算效率。

以下是使用Python实现的斐波那契数列动态规划版本：

def fibonacci(n):
    if n <= 1:
        return n
    cache = [0] * (n + 1)
    cache[1] = 1
    for i in range(2, n + 1):
        cache[i] = cache[i - 1] + cache[i - 2]
    return cache[n]

这段代码中，我们使用了一个列表`cache`作为缓存，存储已经计算过的斐波那契数，避免了重复计算。随着循环的进行，我们逐步构建出一个完整的斐波那契数列。

通过引入循环和缓存机制，我们将时间复杂度从指数级降低到了线性级别。动态规划的应用案例充分展示了如何通过循环优化技术提高算法效率。

## 3.2 分治法与循环优化

### 3.2.1 分治法的原理

分治法（Divide and Conquer）是一种算法设计策略，它将一个问题拆分成若干个规模较小但类似于原问题的子问题，分别解决这些子问题，然后将子问题的解合并以得到原问题的解。分治法的关键在于“分”、“治”、“合”。

- **分**：将原问题划分成一系列子问题。
- **治**：递归地解决各个子问题。
- **合**：将子问题的解合并为原问题的解。

在循环结构中，我们通常在“治”的步骤使用循环来处理子问题，并在“合”的步骤中使用循环来合并解。

### 3.2.2 分治策略在循环优化中的实践

归并排序是一个典型的分治法应用实例。归并排序的基本思想是将数组分成两半，对每一半递归地应用归并排序，最后将排序好的两半合并在一起。

以下是Python实现的归并排序算法：

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left_half = merge_sort(arr[:mid])
    right_half = merge_sort(arr[mid:])
    return merge(left_half, right_half)

def merge(left, right):
    result = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result.extend(left[i:])
    result.extend(right[j:])
    return result

在这个例子中，`merge_sort`函数负责分，`merge`函数负责合。通过递归的方式，我们不断将数组分成更小的部分进行排序，并在每一步使用循环将子数组合并成有序数组。

## 3.3 贪心算法与循环优化

### 3.3.1 贪心算法的逻辑与特点

贪心算法（Greedy Algorithm）是一类在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。

贪心算法解决问题的特点是：
- **局部最优**：每步都选择局部最优解。
- **贪心选择性质**：所选局部最优解能够决定最终解。
- **无回溯**：一旦选择了某个局部最优解，就不会再撤销。

在循环优化中，贪心算法可以有效地简化问题的复杂度，特别是在需要迭代优化的场景中。

### 3.3.2 贪心算法在循环优化中的具体应用

一个经典的贪心算法问题是找零问题：给定一组硬币的面值，以及需要支付的金额，求最少需要多少硬币。

以下是使用Python实现的找零问题的贪心算法：

def min_coins(coins, amount):
    coins.sort(reverse=True)
    result = 0
    for coin in coins:
        while amount >= coin:
            amount -= coin
            result += 1
    return result

在这段代码中，我们首先对硬币进行降序排序，然后使用循环迭代地从最大面值的硬币开始，尽可能多地使用当前面值的硬币，直到支付金额为零。贪心算法的局部最优选择（使用最大面值的硬币）在这里保证了全局最优解（最少硬币数）。

通过这个例子，我们可以看到，贪心算法结合循环可以在某些问题上提供高效且简洁的解决方案。

以上，我们探索了动态规划、分治法、贪心算法在循环优化中的具体应用。这些策略可以帮助我们针对特定类型的问题，设计出更加高效、简洁的算法。下一章，我们将深入探讨循环算法优化的高级策略。

# 4. 循环算法优化的高级策略

## 4.1 空间换时间：缓存机制的运用

### 缓存的概念与重要性

在处理循环算法时，缓存技术是一种常用且有效的优化策略，其核心思想是利用额外的空间来存储已经计算或访问过的结果，从而避免在后续的循环迭代中重复计算，达到降低时间复杂度的目的。缓存的概念本质上是一种时间与空间权衡（Time-Space Tradeoff）的体现。通过消耗一定的内存空间来存储中间结果，换取算法执行效率的提升。

在现代计算机体系结构中，缓存是一种重要的性能优化工具。处理器访问内存的速度远低于其处理数据的速度。因此，处理器拥有若干层级的缓存，以快速读取常用数据。缓存的原理同样可以应用于软件层面的循环算法优化中。

### 缓存策略在循环算法中的应用

缓存策略在循环算法中的应用涉及数据局部性原理，包括时间局部性和空间局部性。时间局部性指的是，如果一个数据项被访问，那么在不久的将来，它很可能再次被访问；空间局部性指的是，如果一个数据项被访问，那么它附近的其他数据项也可能很快被访问。

在实现缓存策略时，关键是要确定什么样的数据值得被缓存。对于循环算法而言，通常是对重复使用的结果进行缓存。例如，在计算斐波那契数列时，可以将已经计算出的结果存储在一个数组中，并在计算新的斐波那契数之前检查缓存中是否已有此结果，以避免重复计算。

# 使用缓存优化斐波那契数列计算
def fibonacci(n, cache={}):
    if n in cache:  # 检查是否已有计算结果
        return cache[n]
    if n <= 2:
        return 1
    cache[n] = fibonacci(n-1, cache) + fibonacci(n-2, cache)  # 存储计算结果
    return cache[n]

# 执行计算
print(fibonacci(100))

在上述代码中，`cache`字典用于存储已经计算过的斐波那契数，避免了重复计算，显著提升了算法效率。需要注意的是，在实现缓存时，要考虑到缓存的内存占用和查找时间，以确保缓存的效率。例如，如果缓存空间过大，可能会导致内存不足，而缓存查找时间过长，则会抵消掉算法优化的效果。

## 4.2 并行与并发处理

### 并行计算的原理

并行计算是一种通过同时使用多个计算资源来解决计算问题的方法。在循环算法优化中，通过引入并行处理，可以将原本需要顺序执行的多个循环迭代分解成可以并行执行的任务，从而利用多核处理器的能力，显著缩短程序运行时间。

并行计算的原理在于将大任务拆分为小任务，然后在不同的处理单元（如CPU核心）上并行处理这些小任务。这要求算法设计者能够识别出可以独立执行的任务，并且设计合适的同步机制来确保数据一致性。

### 循环算法中的并行与并发实践

在实际的循环算法优化中，实现并行化的一个常见方法是数据并行。数据并行指的是将数据集分割成多个部分，每个部分由不同的线程或进程并行处理，处理结果最终合并。

以Python为例，可以使用多线程或多进程模块来实现循环的并行处理。以下是一个简单的多线程并行计算斐波那契数列的例子：

from concurrent.futures import ThreadPoolExecutor
import time

def fibonacci(n):
    if n <= 2:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)

def parallel_fibonacci(n, workers=4):
    if n <= 2:
        return 1
    with ThreadPoolExecutor(max_workers=workers) as executor:
        f1 = executor.submit(fibonacci, n-1)
        f2 = executor.submit(fibonacci, n-2)
        return f1.result() + f2.result()

start_time = time.time()
result = parallel_fibonacci(30)
print("Result:", result)
print("Time taken: {:.2f} seconds".format(time.time() - start_time))

在上述代码中，我们使用了`ThreadPoolExecutor`来创建多个线程并行执行计算。这种方法对于计算密集型任务（如递归计算斐波那契数列）可以显著减少执行时间。然而，并行计算也引入了额外的开销，如线程管理、线程间通信和同步等，这些都需要在优化时考虑。

并行计算的一个关键挑战是处理好线程安全问题，特别是在循环中访问共享资源时。在并行环境中，需要合理设计数据结构和同步机制，比如使用锁（Locks）或原子操作（Atomic operations），以防止数据竞争。

## 4.3 智能算法在循环优化中的应用

### 机器学习与数据挖掘技术

智能算法是指那些能够从大量数据中学习并作出决策的算法。在循环优化中，机器学习技术可以用于预测循环中的关键性能指标，从而指导循环的执行策略。数据挖掘技术则可以帮助我们分析循环的行为，识别性能瓶颈，为优化提供数据支持。

例如，在处理复杂的计算任务时，我们可以使用机器学习模型来预测不同循环迭代的执行时间，并据此调整任务分配策略，以达到负载均衡和性能最大化的目标。

### 智能算法对循环优化的贡献

智能算法在循环优化中的应用，主要体现在两个方面：一是通过机器学习模型自动化地调整循环控制参数；二是在循环执行过程中动态地调整计算策略。

以下是一个使用机器学习模型预测循环性能参数，并根据预测结果动态调整循环参数的简化示例：

import numpy as np
from sklearn.linear_model import LinearRegression

# 假设我们有一组循环迭代性能数据，包括迭代次数和执行时间
# 这里使用随机数据来模拟
iterations = np.array([10, 20, 30, 40, 50]).reshape(-1, 1)
execution_times = np.array([1.2, 2.5, 3.9, 5.2, 6.6])

# 创建线性回归模型
model = LinearRegression()
model.fit(iterations, execution_times)

# 预测某次迭代的执行时间
predicted_time = model.predict(np.array([[60]]))
print(f"Predicted execution time for 60 iterations: {predicted_time[0]}")

在上述例子中，我们使用线性回归模型来预测循环迭代次数对执行时间的影响。在实际应用中，可以使用更为复杂的模型来拟合更复杂的性能曲线，并实时调整循环控制参数，如迭代次数、任务分配等。

当然，智能算法本身也可能成为资源消耗大户，在优化循环算法时需要谨慎使用，权衡算法性能与计算资源的消耗，确保优化的总体收益是正面的。

# 5. 总结与前瞻：循环算法优化的未来趋势

随着计算需求的增长和技术的不断进步，循环算法优化已经成为推动IT行业进步的关键因素之一。尽管已经取得了一定的成果，但仍然面临着一系列挑战。在这一章中，我们将回顾循环优化的成果与挑战，并展望其未来的发展趋势。

## 5.1 循环算法优化的成果与挑战

### 5.1.1 当前循环优化的成效总结

循环算法优化的成效主要体现在以下几个方面：

1. **性能提升**：优化后的循环算法在处理大数据量时表现出色，执行效率显著提升。
2. **资源消耗降低**：通过改进算法逻辑和数据结构的选择，循环算法在内存和处理器使用上更为高效。
3. **可维护性增强**：清晰和优化的代码结构提高了软件的可维护性，便于团队协作和长期开发。

下面的表格详细列出了循环优化前后对比：

| 指标 | 优化前 | 优化后 |
|----------------|--------|--------|
| 执行时间 | 500ms | 200ms |
| 内存占用 | 150MB | 70MB |
| 处理器占用率 | 80% | 30% |
| 代码行数 | 1000 | 600 |

### 5.1.2 面临的技术挑战与发展障碍

然而，循环算法优化也面临着一些挑战：

1. **复杂度管理**：对于高度复杂的循环逻辑，算法的复杂度管理变得异常困难。
2. **硬件兼容性**：优化后的算法可能需要特定的硬件支持，而这可能限制了算法的广泛应用。
3. **算法稳定性**：在极端条件下，优化算法可能表现出不稳定或不可预测的行为。

## 5.2 循环算法优化的未来方向

### 5.2.1 新兴技术趋势对循环优化的影响

未来循环算法优化可能会受到以下新兴技术的影响：

1. **量子计算**：量子计算的出现将彻底改变算法设计的根本。
2. **机器学习**：利用机器学习对算法进行自动优化，可能成为突破性进展。
3. **异构计算**：利用CPU、GPU等多种处理器的协同工作，进一步提升循环算法的效率。

### 5.2.2 未来研究与技术发展的展望

未来的循环算法优化研究可能会关注以下几个方向：

1. **自适应算法**：算法能够根据输入数据和运行环境的变化自适应调整。
2. **并行计算优化**：进一步提高并行计算的效率，减少同步和通信开销。
3. **能量效率**：在保证算法性能的同时，降低能耗，提高能效比。

通过本章的分析，我们可以看到循环算法优化已经取得了一定的成就，但在未来，随着技术的发展和需求的增加，我们仍有许多工作要做。无论是面对挑战还是抓住新机遇，循环算法优化都将为IT行业的发展提供持久的动力。