Sobel算子深度剖析：理解边缘检测的基石算法，提升图像处理技能

# 1. 边缘检测概述**

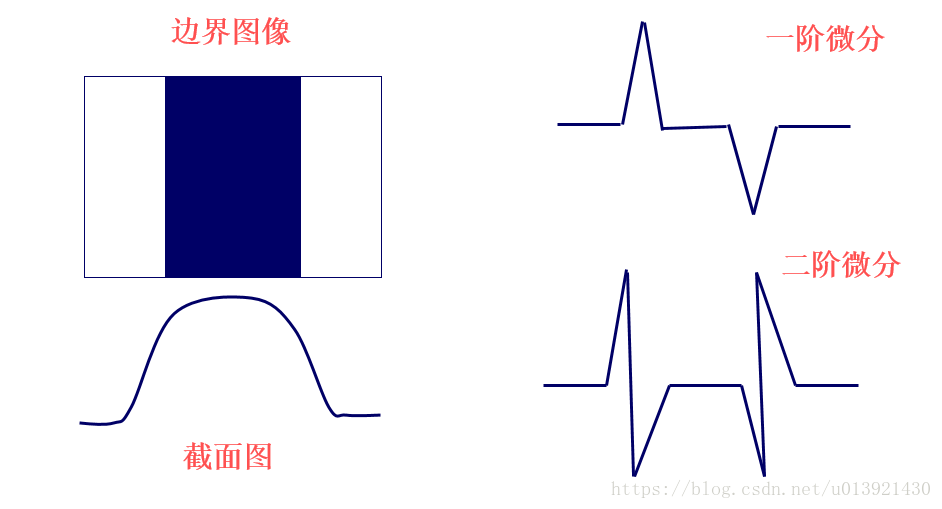
边缘检测是图像处理中一项基本技术，用于识别图像中亮度或颜色发生剧烈变化的区域。边缘通常对应于图像中物体的边界或纹理的变化。边缘检测算法可以帮助提取图像中的重要特征，用于后续的图像分析和理解任务。

在边缘检测算法中，Sobel算子是一种广泛使用的算子，它以其简单、快速和有效性而闻名。Sobel算子通过计算图像中每个像素的梯度来检测边缘。梯度是一个向量，它表示像素亮度在水平和垂直方向上的变化率。通过计算梯度的幅度和方向，Sobel算子可以识别图像中亮度变化剧烈的区域，这些区域通常对应于边缘。

# 2. Sobel算子理论基础

### 2.1 Sobel算子的原理和数学公式

Sobel算子是一种基于一阶差分的边缘检测算法，它通过计算图像中像素点周围像素点的梯度来检测边缘。Sobel算子包含两个模板，分别用于计算水平梯度和垂直梯度。

**2.1.1 梯度计算**

水平梯度和垂直梯度分别通过以下模板计算：

Gx = [[-1, 0, 1],
      [-2, 0, 2],
      [-1, 0, 1]]

Gy = [[-1, -2, -1],
      [0, 0, 0],
      [1, 2, 1]]

对于图像中的每个像素点，将这两个模板与像素点及其周围的像素点进行卷积运算，得到水平梯度和垂直梯度。

**2.1.2 方向计算**

梯度幅度和方向可以通过以下公式计算：

梯度幅度 = sqrt(Gx^2 + Gy^2)
梯度方向 = arctan(Gy / Gx)

梯度幅度表示边缘的强度，梯度方向表示边缘的方向。

### 2.2 Sobel算子的优点和局限性

**2.2.1 优点：**

* **简单、快速、有效：**Sobel算子计算简单，执行速度快，在边缘检测中表现良好。
* **对噪声鲁棒性较好：**Sobel算子使用一阶差分，对图像噪声有一定的鲁棒性。

**2.2.2 局限性：**

* **对噪声敏感：**虽然Sobel算子对噪声有一定的鲁棒性，但对于高噪声图像，仍可能产生虚假边缘。
* **不能检测所有边缘：**Sobel算子只能检测垂直或水平边缘，对于斜边缘的检测效果较差。

# 3. Sobel算子实践应用

### 3.1 图像预处理

在应用Sobel算子进行边缘检测之前，通常需要对图像进行预处理，以提高边缘检测的准确性和鲁棒性。图像预处理主要包括以下两个步骤：

#### 3.1.1 灰度转换

对于彩色图像，需要将其转换为灰度图像，因为Sobel算子只能处理灰度图像。灰度转换可以通过以下公式实现：

gray_image = 0.299 * red_channel + 0.587 * green_channel + 0.114 * blue_channel

其中，`red_channel`、`green_channel`和`blue_channel`分别表示彩色图像的红色、绿色和蓝色通道。

#### 3.1.2 高斯滤波

高斯滤波是一种平滑滤波器，可以去除图像中的噪声。高斯滤波的卷积核是一个二维正态分布，其形状如下：

[ 1 4 7 4 1 ]
[ 4 16 26 16 4 ]
[ 7 26 41 26 7 ]
[ 4 16 26 16 4 ]
[ 1 4 7 4 1 ]

通过对图像进行高斯滤波，可以有效地去除噪声，同时保留图像中的边缘信息。

### 3.2 Sobel算子边缘检测

图像预处理完成后，就可以应用Sobel算子进行边缘检测了。Sobel算子是一个3x3的卷积核，其水平和垂直方向的卷积核分别如下：

水平卷积核：
[-1 0 1]
[-2 0 2]
[-1 0 1]

垂直卷积核：
[-1 -2 -1]
[ 0  0  0]
[ 1  2  1]

#### 3.2.1 水平梯度和垂直梯度计算

使用水平卷积核和垂直卷积核分别与图像进行卷积，可以得到图像的水平梯度和垂直梯度。水平梯度表示图像中像素在水平方向上的变化，垂直梯度表示图像中像素在垂直方向上的变化。

#### 3.2.2 梯度幅度和方向计算

水平梯度和垂直梯度计算完成后，可以计算梯度幅度和梯度方向。梯度幅度表示像素点的边缘强度，梯度方向表示边缘的方向。

梯度幅度和梯度方向的计算公式如下：

梯度幅度 = sqrt(水平梯度^2 + 垂直梯度^2)
梯度方向 = arctan(垂直梯度 / 水平梯度)

### 3.3 边缘后处理

边缘检测完成后，还需要对边缘进行后处理，以去除噪声和增强边缘。边缘后处理主要包括以下两个步骤：

#### 3.3.1 非极大值抑制

非极大值抑制是一种边缘细化技术，可以去除边缘上的噪声。非极大值抑制的原理是，对于每个像素点，只保留梯度幅度最大的边缘点，而抑制其他边缘点。

#### 3.3.2 双阈值化

双阈值化是一种边缘二值化技术，可以将边缘分为强边缘和弱边缘。双阈值化的原理是，将梯度幅度大于高阈值的边缘点标记为强边缘，将梯度幅度小于低阈值的边缘点标记为弱边缘，介于高阈值和低阈值之间的边缘点标记为噪声。

# 4. Sobel算子进阶应用

### 4.1 Sobel算子在图像分割中的应用

#### 4.1.1 图像分割的原理

图像分割是将图像分解为不同区域或对象的过程，每个区域或对象具有相似的特征，例如颜色、纹理或形状。图像分割在计算机视觉和图像处理中至关重要，因为它可以帮助识别和提取图像中的感兴趣区域。

#### 4.1.2 Sobel算子在图像分割中的作用

Sobel算子可以通过检测图像中的边缘来辅助图像分割。边缘是图像中不同区域或对象的边界，它们通常具有较大的梯度值。Sobel算子可以计算图像中每个像素的梯度幅度和方向，从而生成边缘图。

边缘图可以作为图像分割的输入，帮助算法识别不同区域或对象的边界。例如，在以下代码中，我们使用Sobel算子检测图像中的边缘，然后使用K-Means算法对图像进行分割：

import cv2
import numpy as np

# 读取图像
image = cv2.imread('image.jpg')

# 灰度转换
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 高斯滤波
blur = cv2.GaussianBlur(gray, (5, 5), 0)

# Sobel算子边缘检测
sobelx = cv2.Sobel(blur, cv2.CV_64F, 1, 0, ksize=3)
sobely = cv2.Sobel(blur, cv2.CV_64F, 0, 1, ksize=3)

# 计算梯度幅度和方向
magnitude = np.sqrt(sobelx**2 + sobely**2)
direction = np.arctan2(sobely, sobelx)

# K-Means图像分割
segmented_image = cv2.kmeans(magnitude.reshape(-1, 1), 2)[1].reshape(image.shape)

# 显示分割后的图像
cv2.imshow('Segmented Image', segmented_image)
cv2.waitKey(0)
cv2.destroyAllWindows()

### 4.2 Sobel算子在目标检测中的应用

#### 4.2.1 目标检测的原理

目标检测是识别和定位图像中特定目标的过程。目标检测在计算机视觉中至关重要，因为它可以帮助识别和跟踪图像中的感兴趣对象，例如人脸、行人或车辆。

#### 4.2.2 Sobel算子在目标检测中的作用

Sobel算子可以通过检测图像中的边缘来辅助目标检测。边缘可以帮助识别目标的形状和轮廓，从而帮助算法定位和识别目标。例如，在以下代码中，我们使用Sobel算子检测图像中行人的边缘，然后使用滑动窗口算法检测行人：

import cv2
import numpy as np

# 读取图像
image = cv2.imread('image.jpg')

# 灰度转换
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 高斯滤波
blur = cv2.GaussianBlur(gray, (5, 5), 0)

# Sobel算子边缘检测
sobelx = cv2.Sobel(blur, cv2.CV_64F, 1, 0, ksize=3)
sobely = cv2.Sobel(blur, cv2.CV_64F, 0, 1, ksize=3)

# 计算梯度幅度和方向
magnitude = np.sqrt(sobelx**2 + sobely**2)
direction = np.arctan2(sobely, sobelx)

# 滑动窗口算法目标检测
for window_size in range(100, 200, 10):
    for x in range(0, image.shape[0] - window_size):
        for y in range(0, image.shape[1] - window_size):
            window = magnitude[x:x+window_size, y:y+window_size]
            if np.max(window) > 100:
                cv2.rectangle(image, (x, y), (x+window_size, y+window_size), (0, 255, 0), 2)

# 显示检测到的行人
cv2.imshow('Detected Pedestrians', image)
cv2.waitKey(0)
cv2.destroyAllWindows()

# 5. Sobel算子与其他边缘检测算法的比较

### 5.1 Canny算子

**优点：**

- 具有较强的抗噪能力
- 能检测出更精细的边缘
- 边缘定位准确

**局限性：**

- 计算复杂度较高
- 对参数设置敏感

**与Sobel算子的比较：**

Canny算子在抗噪性和边缘定位精度方面优于Sobel算子，但计算复杂度更高。Sobel算子简单快速，但对噪声敏感，定位精度较低。

### 5.2 Prewitt算子

**优点：**

- 与Sobel算子相似，简单快速
- 对噪声的敏感性低于Sobel算子

**局限性：**

- 边缘检测效果不如Sobel算子
- 方向检测精度较低

**与Sobel算子的比较：**

Prewitt算子在抗噪性方面优于Sobel算子，但边缘检测效果和方向检测精度均不如Sobel算子。

### 算法性能比较

| 算法 | 抗噪性 | 边缘检测效果 | 方向检测精度 | 计算复杂度 |
|---|---|---|---|---|
| Sobel | 低 | 中等 | 中等 | 低 |
| Canny | 高 | 高 | 高 | 高 |
| Prewitt | 中等 | 低 | 低 | 低 |

**选择建议：**

* **抗噪性要求高，边缘定位精度要求高：** Canny算子
* **计算复杂度要求低，边缘检测效果要求中等：** Sobel算子
* **抗噪性要求中等，边缘检测效果要求低：** Prewitt算子