【集合的自定义实现】：深入理解集合背后的数据结构，打造个性化的Set类

# 1. 集合的基本概念与理论基础

集合是数学中一个基本的概念，它描述了一组无序且不重复的元素的组合。在计算机科学领域，集合这一概念被进一步抽象和形式化，形成了数据结构中的集合类型。集合的概念源于数学，但在数据结构的实现中，还需要考虑计算机的存储和计算特性。在集合的基本操作中，包含并集、交集、差集和补集等，这些操作在数据处理、数据库、算法设计等领域有着广泛的应用。

集合在IT行业中的使用也非常广泛，例如，在处理数据时，经常需要使用集合来去除重复的元素；在进行数据库查询时，经常需要用到集合的运算来完成复杂的查询操作。因此，理解集合的基本概念和理论基础，对于IT行业的专业人士来说是十分重要的。在后续章节中，我们会深入探讨集合在数据结构中的实现以及自定义集合类的设计与实现，为读者提供更为具体和深入的了解。

# 2. 常见的集合数据结构分析

### 2.1 数组与链表
数组和链表是两种基础且广泛使用的数据结构，在集合的实现中扮演着关键角色。虽然它们在存储方式和操作效率上有明显的差异，但都是构建更复杂数据结构的基石。

#### 2.1.1 数组的基本特性与应用场景
数组是一种线性数据结构，通过索引直接访问元素，具有固定大小。其内部元素在内存中是连续存放的，因此数组在访问操作上具有很高的效率，但其缺点是插入和删除操作效率较低，因为这需要移动后续元素以填补或腾出空间。

数组的典型应用场景包括：
- 实现栈和队列：利用数组的固定大小特性，通过索引来实现先进先出（FIFO）和后进先出（LIFO）的数据结构。
- 作为其他数据结构的基础：如矩阵和多维数组。
- 存储固定大小的数据集合，如日历、颜色编码等。

代码示例：

int[] numbers = new int[10]; // 初始化一个大小为10的整型数组
numbers[0] = 1; // 通过索引直接访问和赋值

#### 2.1.2 链表的结构特点及优缺点
链表由一系列节点组成，每个节点包含数据部分和指向下一个节点的引用。由于链表的节点不需连续存储，它在插入和删除操作上表现出色，不需要移动数据，但访问速度较慢，需要从头节点开始遍历。

链表的典型应用场景包括：
- 实现队列和双向队列：通过调整指针来快速完成插入和删除。
- 构建图数据结构：节点间的连接可以灵活表示图形关系。
- 实现哈希表的冲突解决：链表可以用来存储具有相同哈希值的元素。

代码示例：

class ListNode {
    int val;
    ListNode next;
    ListNode(int x) { val = x; }
}

ListNode head = new ListNode(1); // 创建链表
head.next = new ListNode(2); // 连接节点

### 2.2 树结构的集合实现
树是一种非线性数据结构，以分支节点的方式组织数据，适用于表达层次和分类关系。树结构特别适合于实现集合的查询和排序操作。

#### 2.2.1 二叉树的基本原理及其对集合的支持
二叉树是树结构中最常见的一种形式，每个节点最多有两个子节点。二叉树的遍历操作效率较高，其中最著名的是二叉搜索树（BST），它支持高效的搜索、插入和删除操作。

二叉树的典型应用场景包括：
- 二叉搜索树：可以快速实现集合的搜索、插入和删除操作。
- 平衡二叉树（AVL树）、红黑树等：用于确保树的高度平衡，减少搜索时间。

代码示例：

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

TreeNode root = new TreeNode(1); // 创建根节点
root.left = new TreeNode(2); // 插入左子节点
root.right = new TreeNode(3); // 插入右子节点

### 2.3 哈希表的应用与原理
哈希表是一种通过哈希函数来处理数据的存储结构，它通过直接计算数据项的存储位置，以达到快速存取的效果。

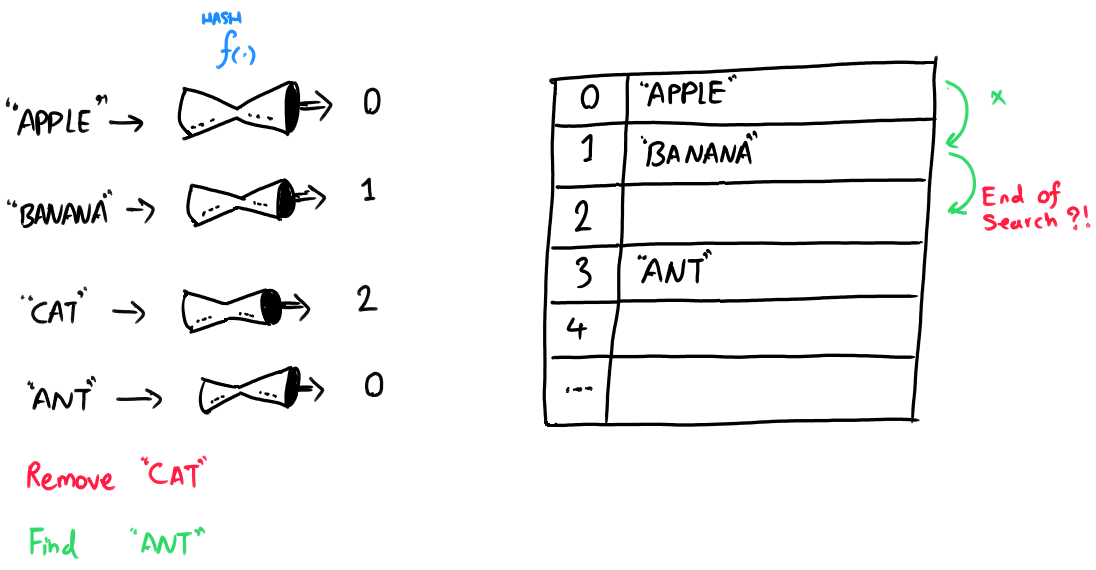
#### 2.3.1 哈希表的结构和冲突解决机制
哈希表由一系列桶（bucket）组成，数据项通过哈希函数映射到不同的桶中。当发生哈希冲突时（即不同的数据项映射到同一个桶），需要通过特定的冲突解决策略，如链表法或开放寻址法，来处理。

哈希表的典型应用场景包括：
- 实现关联数组：通过键值对快速存取数据。
- 作为缓存机制：快速检索和更新频繁访问的数据。

代码示例：

class HashTable {
    private Entry[] table; // 桶数组
    private int capacity; // 哈希表的容量

    class Entry {
        int key;
        int value;
        Entry next; // 链表法处理冲突时使用
    }

    public int get(int key) {
        int hash = (key % capacity); // 计算哈希值
        for (Entry e = table[hash]; e != null; e = e.next) {
            if (e.key == key) return e.value; // 查找成功返回值
        }
        return -1; // 查找失败返回-1
    }
}

#### 2.3.2 哈希表在集合中的应用及其效率分析
哈希表广泛应用于集合实现中，如Java中的`HashMap`和`HashSet`。它能够以接近O(1)的时间复杂度进行数据项的存取。然而，哈希表的空间利用率和性能受到哈希函数、表的大小和负载因子的影响。

哈希表的性能主要取决于：
- 哈希函数的设计：决定了数据项的分布均匀性，影响冲突的频率。
- 表的大小和负载因子：负载因子过大，可能导致性能下降，因此适时的调整表的大小很重要。

通过合理设计哈希表，可以在集合操作中获得极高的效率，对于需要快速访问数据的应用场景，如数据库索引、缓存系统等具有巨大的优势。

# 3. 自定义集合类的设计与实现

## 3.1 类的结构设计与属性定义

### 3.1.1 如何定义集合类的属性和方法

设计一个自定义集合类的首要步骤是对类的属性和方法进行定义。集合类通常用于存储一组数据项，并提供添加、删除、查找等基本操作。在定义属性时，需要考虑如何存储集合元素、集合的容量限制、集合的状态（是否允许重复元素、是否有序等）。

例如，如果我们设计一个简单的有序集合类，我们可以定义如下属性：

- `elements`: 用于存储集合中的元素。
- `size`: 集合中当前元素的数量。
- `capacity`: 集合的最大容量（可选，用于固定大小的集合）。

对于方法，我们需要实现一些集合操作的函数：

- `add`: 添加一个元素到集合中。
- `remove`: 从集合中移除一个元素。
- `find`: 在集合中查找一个元素。
- `isEmpty`: 检查集合是否为空。
- `size`: 获取集合中元素的数量。

### 3.1.2 类内部数据的存储策略选择

集合类的内部数据存储策略是决定其性能的关键因素之一。常见的存储策略包括数组、链表、二叉树、哈希表等。每种策略都有其优势和劣势，例如：

- **数组**适合于元素大小固定且数量有限的情况，优点是访问速度快，缺点是插入和删除操作较慢，且空间可能浪费。
- **链表**适合于元素大小不定的情况，优点是插入和删除操作较快，缺点是查找元素较慢。
- **树结构**如二叉搜索树，适合于需要有序排列的集合，优点是查找、插入和删除操作的效率较高，缺点是维护成本较高，特别是树结构不平衡时。
- **哈希表**适合于快速查找的情况，优点是查找、插入和删除操作的平均时间复杂度为O(1)，缺点是不支持有序排列，且有哈希冲突问题。

在设计自定义集合类时，需要根据实际的应用场景来选择合适的存储策略。例如，如果需要一个有序且可以快速查找的集合，可以选择平衡二叉搜索树；如果需要快速的随机访问，可以选择数组或哈希表。

## 3.2 集合操作的核心方法实现

### 3.2.1 添加、删除和查找操作的算法设计

集合操作的核心在于添加（add）、删除（remove）和查找（find）这三个操作。每个操作的算法设计需要根据集合内部数据的存储策略来定制。下面给出这些操作的基本思路：

#### 添加操作（add）

- **数组存储策略**：检查数组是否有空位，如果有，则将元素添加到数组的末尾，否则需要扩展数组容量并移动现有元素。
- **链表存储策略**：创建一个新节点，将新节点添加到链表的合适位置（头节点或尾节点）。
- **二叉树存储策略**：将新元素添加到树中合适的位置以保持二叉搜索树的特性。
- **哈希表存储策略**：计算元素的哈希值，将元素放置在哈希表的对应位置。

#### 删除操作（remove）

- **数组存储策略**：查找元素的索引位置，将其后所有元素前移一位，并更新元素计数器。
- **链表存储策略**：遍历链表找到元素的前一个节点，更改指针以绕过要删除的节点，然后释放该节点的内存。
- **二叉树存储策略**：找到要删除的节点，并考虑四种情况：节点是叶子节点、只有一个子节点、有两个子节点。
- **哈希表存储策略**：计算元素的哈希值，找到对应位置的元素并移除，同时考虑处理哈希冲突链。

#### 查找操作（find）

- **数组存储策略**：使用线性搜索遍历数组直到找到元素或遍历结束。
- **链表存储策略**：遍历链表，直到找到匹配的节点或遍历结束。
- **二叉树存储策略**：通过比较节点值来递归或迭代地搜索二叉树。
- **哈希表存储策略**：直接通过哈希值定位元素，处理哈希冲突。

### 3.2.2 集合的合并、差集等高级操作实现

除了基本的添加、删除和查找操作之外，集合类还通常需要实现一些高级操作，例如合并两个集合（union）、计算两个集合的差集（difference）、求交集（intersection）等。以下是这些操作