【集合与排序的巧妙结合】：探索集合的有序性及高效排序方法

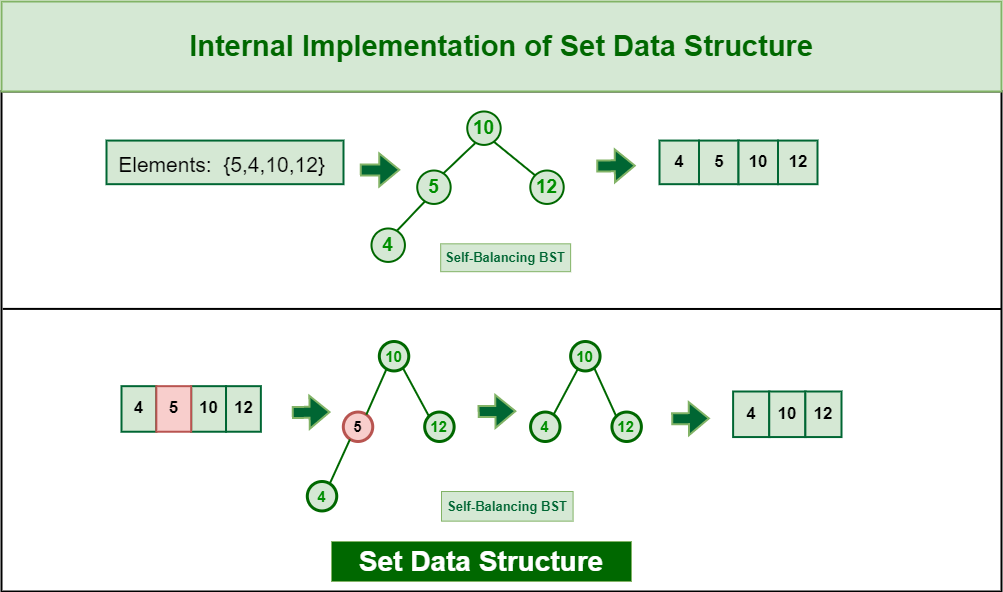
# 1. 集合与排序的基本概念

在开始探讨集合和排序的进阶内容之前，我们必须首先理解这些基本概念的含义及其重要性。集合是数学中的一个基本概念，它是由不同的元素组成的整体。在编程领域，集合常常与数据结构相结合，用于存储不重复的数据项。了解集合的基本操作和性质，对于任何希望提升数据处理能力的IT专业人员来说都是必不可少的。

排序是将一组数据按照一定的顺序进行排列的过程。它广泛应用于计算机科学和数据分析领域。良好的排序算法可以提高数据检索的效率，优化存储空间，甚至在某些情况下减少数据处理时间。在深入探讨排序算法之前，建立对排序目的、应用场景和基本原理的理解是非常关键的。

以下简要回顾一下排序和集合的基本概念：

- **集合**：数学中的一组元素的聚合，具有无序性和元素唯一性。
- **排序**：数据处理方法，将集合中的元素按照特定的顺序重新排列。
- **应用**：在数据处理和数据库管理系统中，集合和排序是构建高效算法的基础。

在后续的章节中，我们将探讨集合与排序算法的更深层次的理论基础以及它们在实际应用中的表现和优化策略。我们将从集合的基础理论出发，逐步深入了解排序算法的分类、特点、性能评估以及在不同场景下的应用案例。通过本章的学习，读者应能掌握集合与排序的基本概念，并为深入研究打下坚实的基础。

# 2. 集合有序性的理论基础

### 2.1 集合理论的基本原理

#### 2.1.1 集合的定义与性质

集合是一个数学概念，它描述了一组明确且不同的对象的总体。这些对象称为集合的元素。在数学中，集合通常用大写字母表示，如A、B、C等，而集合中的元素则用小写字母表示。一个基本的集合表达式可以是 A = {1, 2, 3}，这里1、2、3是集合A的元素。

集合理论中的一些基本性质包括：

- **无序性**：集合中的元素没有特定的顺序。
- **唯一性**：集合中不允许出现重复的元素。
- **可比较性**：任意两个集合要么完全相同，要么完全不同，不存在部分相同的概念。

#### 2.1.2 集合运算及其规则

集合运算主要包括以下几种：

- **并集**：集合A和B的并集包含在A或B中的所有元素。用符号表示为 A ∪ B。
- **交集**：集合A和B的交集只包含同时在A和B中的元素。用符号表示为 A ∩ B。
- **差集**：集合A对B的差集包含在A中但不在B中的元素。用符号表示为 A - B 或 A \ B。
- **补集**：集合A的补集包含所有不在A中的元素，通常是在一个更广泛的全集中定义的。用符号表示为 A' 或 C(A)。
- **笛卡尔积**：集合A和B的笛卡尔积是所有可能的有序对(a, b)的集合，其中a属于A且b属于B。用符号表示为 A × B。

集合运算遵循一些基本的规则，例如交换律、结合律、分配律等。这些规则对于简化集合表达式和解决集合相关问题非常有用。

### 2.2 排序算法的分类与特点

#### 2.2.1 常见排序算法简介

排序算法是指将一组数据按照特定顺序（通常是从小到大或从大到小）进行排列的算法。以下是几种常见的排序算法简介：

- **冒泡排序**：通过重复遍历待排序的列表，比较每对相邻元素，并在必要时交换它们。每次遍历后，最大的元素会被放置在正确的位置。
- **选择排序**：工作原理是在每一回合中选出最小的元素，然后与该回合的第一个位置的元素交换。
- **插入排序**：通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
- **快速排序**：通过选取一个基准值，将数组分为两部分，其中一部分的所有数据都比另一部分的所有数据要小，然后递归地在子数组上重复这个过程。
- **归并排序**：采用分治法的一个典型应用。将已有序的子序列合并，得到完全有序的序列。

#### 2.2.2 时间复杂度和空间复杂度分析

排序算法的效率通常用时间和空间复杂度来衡量。复杂度分析关注算法执行时间随着输入数据规模增长的趋势。

- **时间复杂度**：描述了算法执行时间与输入数据规模之间的关系。常见的时间复杂度有O(1)、O(log n)、O(n)、O(n log n)、O(n^2)等。
- **空间复杂度**：衡量算法在执行过程中临时占用存储空间大小的量度，主要考虑算法执行过程中需要的额外空间。

下面是一个表格展示了上面提到的几种排序算法在最坏、平均和最好情况下的时间复杂度和空间复杂度：

| 排序算法 | 最坏时间复杂度 | 平均时间复杂度 | 最好时间复杂度 | 空间复杂度 |
|------------|----------------|----------------|----------------|------------|
| 冒泡排序 | O(n^2) | O(n^2) | O(n) | O(1) |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) |
| 插入排序 | O(n^2) | O(n^2) | O(n) | O(1) |
| 快速排序 | O(n^2) | O(n log n) | O(n log n) | O(log n) |
| 归并排序 | O(n log n) | O(n log n) | O(n log n) | O(n) |

### 2.3 排序算法的稳定性和比较性

#### 2.3.1 稳定排序的概念及重要性

在排序算法中，“稳定性”是一个重要的概念。稳定排序算法指的是在排序过程中保持相等元素的相对顺序不变的算法。

举个例子，如果我们有一个记录列表，其包含的数据项有主键和次键两个属性，如果使用稳定的排序算法，那么当主键相同的情况下，次键的相对顺序将保持不变。

稳定排序在某些应用场景中非常重要，如在数据库索引中排序时，保持记录的相对位置不变，有助于保持数据的一致性和预测性。