基于混淆矩阵的F1分数计算方法详解

# 1. 导言

在机器学习和数据分析领域，混淆矩阵和F1分数是评估模型性能不可或缺的工具。混淆矩阵提供了模型在分类问题中预测结果的详细信息。而F1分数则是综合考虑模型的准确率和召回率，更全面地评估模型的表现。了解混淆矩阵和F1分数的概念及计算方法，对于改进模型和优化预测结果至关重要。

通过本文的详细介绍和案例分析，读者将能够深入理解混淆矩阵的构造和评估指标的含义，以及如何利用F1分数来评估模型的性能。同时，本文还将探讨F1分数在不同领域的应用场景和实际案例，帮助读者更好地应用这一评估指标解决实际问题。深入了解和应用混淆矩阵和F1分数，将有助于提升数据科学家和机器学习工程师的技能水平。

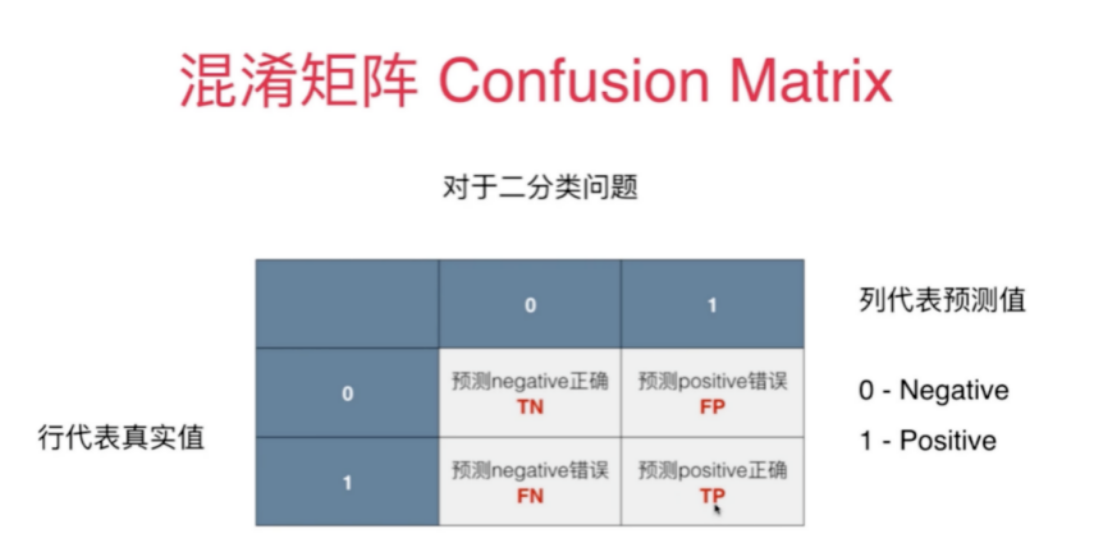
# 2. **混淆矩阵与评估指标**

在机器学习中，为了评估模型的性能和效果，常常会使用混淆矩阵和相关评估指标。这些指标可以帮助我们更好地了解模型在处理数据时的表现。

#### 2.1 真正率、假正率与其他基本概念

- **真正率(TP Rate)**：指被模型正确划分为正类别的样本数占总正类别样本数的比例，计算公式为 $TPR = \frac{TP}{TP + FN}$。
- **假正率(FP Rate)**：指被模型错误划分为正类别的负类别样本数占总负类别样本数的比例，计算公式为 $FPR = \frac{FP}{FP + TN}$。
- 其他基本概念：真负率(TNR)、假负率(FNR)等，通过混淆矩阵中的四个基本计数单元来计算。

#### 2.2 准确率与召回率的定义

- **准确率(Precision)**：指模型预测为正例的样本中，真正例的比例，计算公式为 $Precision = \frac{TP}{TP + FP}$。

- **召回率(Recall)**：指所有正例样本中，被模型正确预测为正例的比例，计算公式为 $Recall = \frac{TP}{TP + FN}$。

#### 2.3 精确度、灵敏度和特异度的意义

- **精确度(Accuracy)**：指模型预测正确的样本数占总样本数的比例，计算公式为 $Accuracy = \frac{TP + TN}{TP + TN + FP + FN}$。

- **灵敏度(Sensitivity)**：又称为召回率，指模型对正例的判断能力，计算公式为 $Sensitivity = \frac{TP}{TP + FN}$。

- **特异度(Specificity)**：指模型对负例的判断能力，计算公式为 $Specificity = \frac{TN}{TN + FP}$。

以上这些基本概念和指标构成了混淆矩阵中各种评估模型性能的要素，对于理解模型的分类效果至关重要。

# 3. F1分数的计算方法详解

#### 3.1 F1分数的定义
在机器学习领域，F1分数是综合考虑了准确率和召回率的指标，常用于评估分类模型的性能表现。它是精确率和召回率的调和均值，能够更全面地评估模型在正负样本预测上的表现。

#### 3.2 精确度和召回率的权衡
精确率衡量了模型在所有预测为正类别中