解决复杂优化问题，寻找最优解：MATLAB优化算法，让你成为优化算法专家

# 1. MATLAB优化算法简介

MATLAB优化算法是MATLAB中用于求解优化问题的工具集。优化问题涉及找到一组变量的值，使目标函数最大化或最小化，同时满足约束条件。MATLAB优化算法提供了一系列功能强大的算法，可以高效地解决各种优化问题。

优化算法通常分为两大类：传统优化算法和智能优化算法。传统优化算法基于数学原理，如梯度下降和牛顿法。智能优化算法受生物学和物理现象的启发，如遗传算法和粒子群优化。MATLAB优化算法涵盖了这两种类型的算法，为用户提供了解决广泛优化问题的全面解决方案。

# 2. MATLAB优化算法理论基础

### 2.1 优化问题的数学模型

优化问题是寻找一个函数的极值（最大值或最小值）的问题。数学上，优化问题可以表示为：

min/max f(x)
subject to:
    g(x) <= 0, h(x) = 0

其中：

- `f(x)` 是目标函数，表示需要优化（最小化或最大化）的函数。
- `x` 是决策变量，表示需要优化的问题变量。
- `g(x) <= 0` 是不等式约束，表示决策变量的限制条件。
- `h(x) = 0` 是等式约束，表示决策变量必须满足的条件。

#### 2.1.1 线性规划模型

线性规划模型是一种特殊的优化问题，其中目标函数和约束条件都是线性的。线性规划模型可以表示为：

min/max c^T x
subject to:
    Ax <= b

其中：

- `c` 是目标函数的系数向量。
- `x` 是决策变量向量。
- `A` 是约束条件系数矩阵。
- `b` 是约束条件右端向量。

#### 2.1.2 非线性规划模型

非线性规划模型是一种优化问题，其中目标函数或约束条件是非线性的。非线性规划模型可以表示为：

min/max f(x)
subject to:
    g(x) <= 0, h(x) = 0

其中：

- `f(x)` 是非线性的目标函数。
- `g(x) <= 0` 是非线性的不等式约束。
- `h(x) = 0` 是非线性的等式约束。

### 2.2 优化算法的分类和原理

优化算法是用于求解优化问题的数学方法。优化算法可以分为两类：

#### 2.2.1 传统优化算法

传统优化算法是基于数学原理的优化算法，包括：

- **梯度下降法：**一种迭代算法，通过沿着目标函数梯度负方向移动来寻找极值。
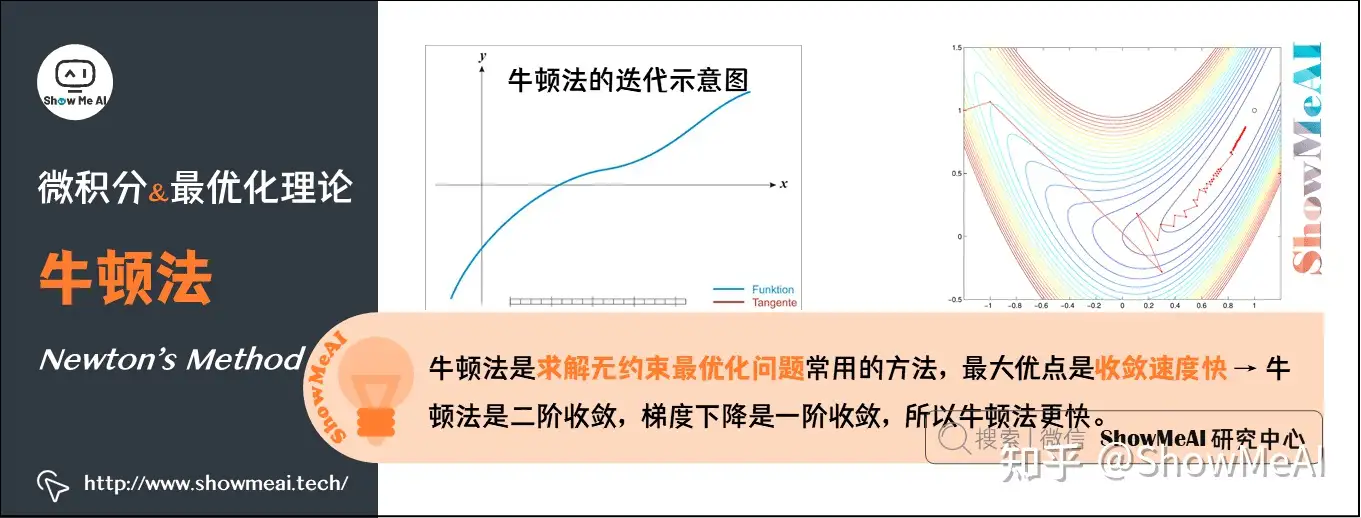
- **牛顿法：**一种二次收敛算法，利用目标函数的二阶导数信息来加速收敛。
- **共轭梯度法：**一种迭代算法，利用共轭梯度方向来加速收敛。

#### 2.2.2 智能优化算法

智能优化算法是受自然界启发的优化算法，包括：

- **遗传算法：**一种模拟生物进化过程的算法，通过选择、交叉和变异操作来优化目标函数。
- **粒子群算法：**一种模拟鸟群觅食行为的算法，通过信息共享和协作来优化目标函数。
- **蚁群算法：**一种模拟蚂蚁觅食行为的算法，通过信息素的传递和更新来优化目标函数。

# 3.1 线性规划问题求解

#### 3.1.1 线性规划问题的建模

线性规划问题是一种数学优化