HALCON图像配准与拼接：案例分析与技术应用


# 摘要
HALCON图像配准与拼接是图像处理领域的重要技术，对于提高图像分析的精度和效果至关重要。本文从理论和实践两个维度出发，全面阐述了图像配准的基础知识、关键算法、性能评估方法以及图像拼接的流程和技术。特别地，详细介绍了HALCON工具在图像配准与拼接中的应用案例，展示了其在实际项目中的有效性。同时，本研究还探讨了高级配准技术、拼接技术的发展方向以及当前面临的技术挑战和可能的解决策略，旨在为图像配准与拼接技术的未来发展提供参考和指导。

# 关键字
HALCON；图像配准；图像拼接；特征点匹配；性能评估；自动化与智能化

参考资源链接：[HALCON_实用教程与案例分析.pdf](https://wenku.csdn.net/doc/6412b4febe7fbd1778d418f5?spm=1055.2635.3001.10343)
# 1. HALCON图像配准与拼接概述

在现代计算机视觉领域中，图像配准与拼接技术是核心组成部分，对于各种视觉处理任务至关重要。图像配准，是指将不同时间、不同视角或不同传感器获取的两幅或更多图像进行空间变换，以达到几何对齐的过程。而图像拼接则是在配准的基础上，将多个图像合并成一幅宽视角或高分辨率的新图像。

HALCON作为一个功能强大的机器视觉软件，提供了丰富的图像处理和分析工具，包括先进的图像配准与拼接功能。通过HALCON，我们可以实现高精度的图像对齐和无缝拼接，广泛应用于医疗成像、卫星遥感、工业检测等领域。

本章将对HALCON在图像配准与拼接领域的应用进行简要介绍，为后续章节详细探讨其理论基础和实践应用打下基础。接下来的章节将深入分析HALCON工具的核心功能，并通过案例研究，探讨如何在实际工作中应用HALCON进行有效的图像配准与拼接。

# 2. 图像配准的理论基础与实践

### 2.1 图像配准的基本概念

#### 2.1.1 配准的定义和重要性

图像配准是指将来自同一场景但采集角度、时间或成像条件不同的两幅或多幅图像按照一定的规则进行空间变换，使得这些图像在空间上的一致性，即对应点间的距离尽可能小。这是图像处理领域中非常重要的一个环节，尤其在图像融合、三维重建、变化检测、医学图像分析等领域发挥着至关重要的作用。

图像配准的重要性体现在，通过配准，可以整合同一场景下的多个视角的信息，得到更丰富或更具解释性的结果。例如，在医学领域，通过对不同时间点拍摄的患者器官图像进行配准，医生可以观察到疾病的进展或治疗的效果。在遥感领域，配准技术使研究者能够对比同一地区在不同时间的卫星图像，分析地表变化。

#### 2.1.2 配准的分类及其适用场景

配准方法主要可以分为刚性配准、仿射配准和非刚性配准。

刚性配准考虑图像间的旋转、平移和镜像，主要用于那些变形很小的场景。例如，在工业视觉检测中，经常要对同一物体在不同时间或角度拍摄的图片进行比对。

仿射配准则允许图像进行缩放、旋转、倾斜等变化，能应对较为复杂的场景变形情况。在多角度拍摄的三维重建项目中，仿射配准能够有效地对齐各角度的图片，构建出较为准确的三维模型。

非刚性配准则允许图像间的局部变形，适用于生物组织的图像配准等需要考虑组织变形和拉伸的复杂场景。比如，在神经成像中，非刚性配准能够很好地补偿大脑在不同状态下的形变，为研究提供准确的数据。

### 2.2 图像配准的关键算法

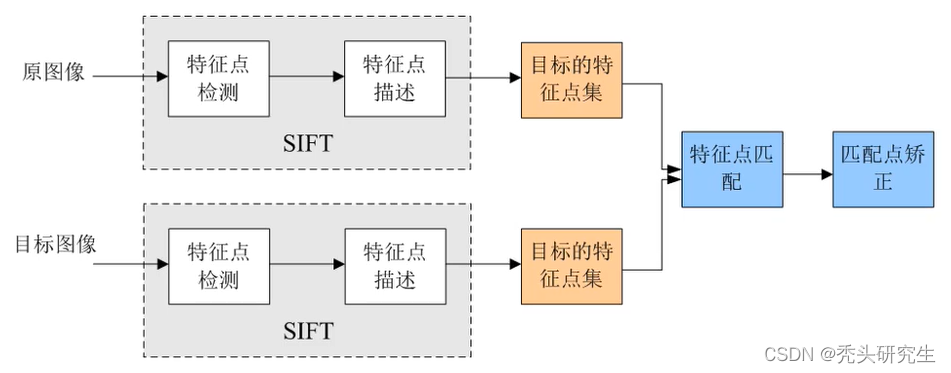
#### 2.2.1 特征点检测与匹配

特征点检测与匹配是图像配准中的重要步骤，涉及到从图像中提取有用的特征，并在不同图像之间寻找对应的特征点。

**SIFT（尺度不变特征变换）**是一种常用于特征点检测的算法，它对旋转、缩放、亮度变化保持不变性，甚至在一定程度上对视角变化和仿射变换也保持不变性。SIFT特征点匹配一般通过计算特征点的欧氏距离来进行，距离最近的两个点通常被认为是匹配的。

代码示例：

import cv2
from matplotlib import pyplot as plt

def find_features_and_match(img1_path, img2_path):
    # 读取图像
    img1 = cv2.imread(img1_path, 0)  # 查询图像
    img2 = cv2.imread(img2_path, 0)  # 训练图像

    # 初始化SIFT检测器
    sift = cv2.SIFT_create()

    # 使用SIFT找到关键点和描述符
    kp1, des1 = sift.detectAndCompute(img1, None)
    kp2, des2 = sift.detectAndCompute(img2, None)

    # 初始化BFMatcher
    bf = cv2.BFMatcher()
    matches = bf.knnMatch(des1, des2, k=2)

    # 使用 Lowe's ratio test 进行匹配
    good_matches = []
    for m, n in matches:
        if m.distance < 0.75 * n.distance:
            good_matches.append(m)

    # 绘制前20个好的匹配
    img3 = cv2.drawMatches(img1, kp1, img2, kp2, good_matches[:20], None, flags=2)
    plt.imshow(img3), plt.show()

# 使用示例
find_features_and_match('image1.jpg', 'image2.jpg')

在上述代码中，我们使用了OpenCV库来实现SIFT算法，并且使用了BFMatcher来进行特征点的匹配。匹配结果被绘制出来，并展示给用户。

#### 2.2.2 变换模型和代价函数

图像配准中，变换模型定义了图像间的几何变换关系，而代价函数衡量了变换后图像之间的差异。

常用的变换模型有仿射变换、透视变换等。仿射变换可以表示为`T(x) = Mx + b`，其中`M`是仿射矩阵，`b`是平移向量。而透视变换的表达更加复杂，适用于相机视角变化引起的图像变形。

**代价函数**是配准算法优化过程中的关键。常见的代价函数有最小二乘法、互信息（Mutual Information）、归一化互相关（Normalized Cross-Correlation, NCC）等。最小二乘法通常用于基于强度的配准，而互信息和NCC多用于基于特征的配准。

#### 2.2.3 最优化配准算法的实现

图像配准的最优化问题通常通过迭代方法来解决，常见的优化算法包括梯度下降法、牛顿法、共轭梯度法等。在这些方法中，我们需要确定一个初始变换矩阵，然后通过优化算法对这个矩阵进行迭代更新，直到达到收敛条件。

在实际应用中，使用优化算法配准时，可以通过设置合适的停止准则来减少计算时间，例如设定最大迭代次数、变换矩阵更新的阈值等。图2-1展示了一个优化过程的示例。

import