【聚类分析深度剖析】：3大策略解锁无监督学习精髓


# 摘要
聚类分析是数据挖掘和无监督学习中的核心技术，旨在将数据集内的相似对象组成多个簇。本文首先概述了聚类分析的基础理论和数学模型，包括无监督学习的定义、聚类算法的目标、距离和相似性度量方法以及聚类准则函数。接着，本文详细解析了层次聚类和部分经典聚类算法如K-means、K-medoids和DBSCAN的原理和步骤。之后，文章深入探讨了聚类结果的评估指标、参数优化策略，并强调了数据预处理和特征选择在聚类分析中的重要性。最后，本文探索了聚类分析在实际应用中的场景，并分析了高维数据聚类的挑战和多源数据的聚类融合方法，同时探讨了深度学习在聚类分析中的新兴应用。

# 关键字
聚类分析；无监督学习；距离度量；层次聚类；参数优化；深度学习

参考资源链接：[数据挖掘实验报告+代码+截图](https://wenku.csdn.net/doc/6412b495be7fbd1778d4017a?spm=1055.2635.3001.10343)
# 1. 聚类分析概述

聚类分析是数据挖掘中的一种重要技术，其核心目标是将数据集中相似的对象分组在一起。通过将相似的数据划分为一个个簇，聚类算法帮助我们发现数据中的模式、结构和关系，无需预先标记数据类别。聚类在市场分析、社交网络分析、图像分割等多个领域都有广泛的应用。

聚类分析可以分为有监督学习和无监督学习。在无监督学习中，由于缺乏先验知识，聚类算法需要从原始数据中自动发现潜在的分布和结构，而无需关注特定的输出。聚类算法的设计和优化涉及多个领域的知识，包括统计学、机器学习和数据科学。

从最简单的划分方法到复杂的层次和基于模型的方法，聚类技术不断发展和演进，以应对不同的数据类型和业务需求。随着技术的不断成熟，聚类分析已经成为数据科学和机器学习领域不可或缺的一部分。

# 2. 理论基础与数学模型

## 2.1 聚类分析的理论框架

### 2.1.1 无监督学习的定义与特点

无监督学习是机器学习的一个分支，它不同于监督学习需要带有标签的训练数据。在无监督学习中，算法试图在没有明确指导的情况下发现隐藏的模式或数据的内在结构。聚类分析是无监督学习中最常见和最重要的任务之一，它涉及到根据相似性将数据点分组，使得同一组内的数据点彼此相似，而不同组的数据点则相对不相似。

聚类分析的特点包括：
- **无标签数据处理**：不需要事先知道数据的类别标签，聚类算法会自动发现数据的内在结构。
- **探索性分析**：在很多情况下，聚类可以作为数据探索的一种方式，帮助研究者理解数据集中的结构和分布。
- **灵活性和多样性**：不同的聚类算法和参数设置可以产生不同的结果，这为研究者提供了从不同角度探索数据的灵活性。

### 2.1.2 聚类的基本概念和目的

聚类的目的是将数据集分割成多个群组，使得每个群组内的数据点相似性高，而群组间的相似性低。聚类结果通常用于数据的进一步分析，例如理解数据的分布、进行数据简化、发现数据中的异常值或寻找数据中的潜在变量。

聚类算法通常涉及以下基本概念：
- **簇（Cluster）**：数据点的集合，簇内的点彼此相似，簇间的点相对不相似。
- **原型（Prototype）**：代表簇中心的一个点，可以是簇内所有点的均值，也可以是一个抽象的点。
- **距离度量（Distance Metric）**：用于衡量数据点之间相似性的方法，如欧氏距离、曼哈顿距离等。
- **相似性（Similarity）**：衡量数据点之间相似程度的指标，一般距离越小，相似性越高。

## 2.2 聚类算法的数学模型

### 2.2.1 距离度量方法

距离度量是聚类分析中的核心概念，它决定了数据点如何在空间中相互比较。不同的距离度量方法会直接影响聚类的结果。以下是几种常见的距离度量方法：

- **欧氏距离（Euclidean Distance）**：两点间直线距离，是最常用的距离度量方法。

  # 欧氏距离的Python代码实现
  import numpy as np

  def euclidean_distance(x, y):
      return np.sqrt(np.sum((x - y) ** 2))

- **曼哈顿距离（Manhattan Distance）**：两点在标准坐标系上的绝对轴距总和。

  # 曼哈顿距离的Python代码实现
  def manhattan_distance(x, y):
      return np.sum(np.abs(x - y))

- **切比雪夫距离（Chebyshev Distance）**：在坐标系上，两点之间的最大距离。

  # 切比雪夫距离的Python代码实现
  def chebyshev_distance(x, y):
      return np.max(np.abs(x - y))

### 2.2.2 相似性度量方法

相似性度量与距离度量相对应，它提供了另一种比较数据点的方法。相似性越高，距离度量值越小。常见的相似性度量包括：

- **余弦相似性（Cosine Similarity）**：度量两个非零向量的夹角大小，通常用于文本数据。

  # 余弦相似性的Python代码实现
  def cosine_similarity(x, y):
      return np.dot(x, y) / (np.linalg.norm(x) * np.linalg.norm(y))

- **杰卡德相似系数（Jaccard Similarity）**：用于度量两个集合的相似度，常用于计算样本集合的相似度。

### 2.2.3 聚类准则函数

聚类准则函数是评价聚类效果好坏的标准，常见的有：

- **最小方差准则（Minimize Variance）**：最小化簇内距离的平方和，以达到簇内紧密的目的。

  # 最小方差准则的Python代码示例
  def minimize_variance(clusters):
      variance = sum([np.sum([np.sum((x - c)**2) for x in cluster]) for cluster, c in clusters])
      return variance

- **最大化间隔准则（Maximize Margin）**：寻找最大的簇间距离，以实现簇间区分最大化。

不同的聚类准则函数将直接影响聚类的算法选择和聚类结果，因此在实际应用中需要根据数据特性和分析目的来选择合适的准则函数。

聚类分析的理论基础与数学模型为理解各种聚类算法提供了必要的理论支撑。通过上述介绍，可以发现聚类的核心概念和方法对于最终的聚类结果具有决定性影响。在选择和设计聚类算法时，务必充分考虑这些理论元素和数学模型的适用性。接下来的章节将详细介绍几种经典的聚类算法，并进一步讨论它们的优缺点以及适用场景。

# 3. 经典聚类算法详解

## 3.1 层次聚类方法

层次聚类通过逐步合并或分割数据点来构建一个分层的聚类树，该方法不依赖于初始的聚类中心，是聚类分析中一种直观且常见的方法。

### 3.1.1 聚类树的构建过程

层次聚类的基本思想是将n个数据对象看作n个单独的类，然后根据对象间的相似性逐步合并，直到所有的对象被合并到一个类中或者满足某个停止条件为止。

构建聚类树的过程可以分为两个主要步骤：

1. **聚合步骤**：开始时，每个数据点都是一个独立的类。在每一步中，距离最近的两个类被合并成一个新的类。这个过程会重复进行，直到满足特定的停止准则。

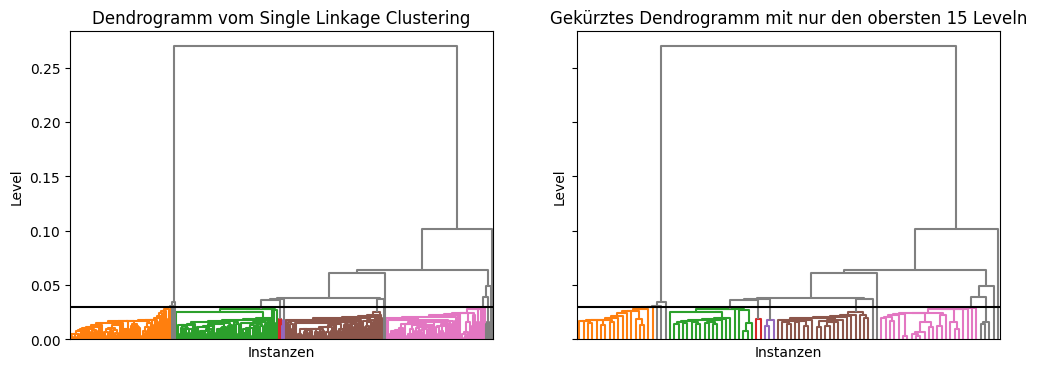
2. **创建聚类树**：通过从聚合过程得到的信息构建一个树状结构，这棵树被称为谱系图（dendrogram）。在谱系图上，水平线段表示类被合并的步骤，高度表示合并时对象间的距离。

层次聚类的两个常见策略为：

- **自底向上（聚合策略）**：也称为AGNES（Agglomerative Nesting）。从单点类开始，逐步合并，直到形成一个包含所有点的单一类。
- **自顶向下（分裂策略）**：也称为DIANA（Divisive Analysis）。从包含所有点的单一类开始，逐步分裂，直到每个点成为一个单独的类。

### 3.1.2 分层方法的优缺点分析

层次聚类方法的优点主要包括：

- **不需要预先指定聚类的数量**：聚类树会自然地展示出数据可以被分为多少个聚类，这一点对探索性数据分析非常有用。
- **直观且易于解释**：通过谱系图可以直观地看到数据如何聚在一起，为分析提供直观的可视化结果。

然而，层次聚类也存在一些缺点：

- **计算复杂度高**：对于大数据集，层次聚类可能会非常耗时，因为它通常具有O(n^3)的计算复杂度。
- **无法回溯**：一旦类被合并或分割，就无法撤销操作，可能不是最优的