【常见错误揭秘】：假设检验中第一类与第二类错误的识别与预防

# 1. 假设检验的基本概念与类型

## 1.1 假设检验的定义
假设检验是一种统计方法，用于评估两个假设之间的证据。在统计学中，我们通常将“无效假设”（null hypothesis, H₀）和“替代假设”（alternative hypothesis, H₁）进行对比。无效假设是指无差异、无效应的假设，而替代假设指的是我们希望证实的效果或差异。通过收集数据并计算检验统计量，我们可以决定是否拒绝无效假设。

## 1.2 假设检验的流程
假设检验的流程一般包括以下步骤：
1. 提出无效假设和替代假设。
2. 确定检验统计量和显著性水平（α）。
3. 根据样本数据计算检验统计量。
4. 根据检验统计量和显著性水平做出决策：拒绝或不拒绝无效假设。

## 1.3 假设检验的类型
假设检验的类型根据数据的分布和检验的目标不同而分为多种，其中常见的包括：
- 参数检验，如t检验、z检验和ANOVA（方差分析）。
- 非参数检验，如曼-惠特尼U检验、威尔科克森符号秩检验。
- 单尾检验与双尾检验：这取决于我们对假设检验的方向性预期。

假设检验是数据分析中的重要工具，它帮助我们科学地判断数据中是否存在统计意义上的证据，以此来支持或反对我们关于总体参数的假设。

# 2. 深入解析第一类错误

## 2.1 第一类错误的定义与影响

### 2.1.1 犯第一类错误的概率α和其含义

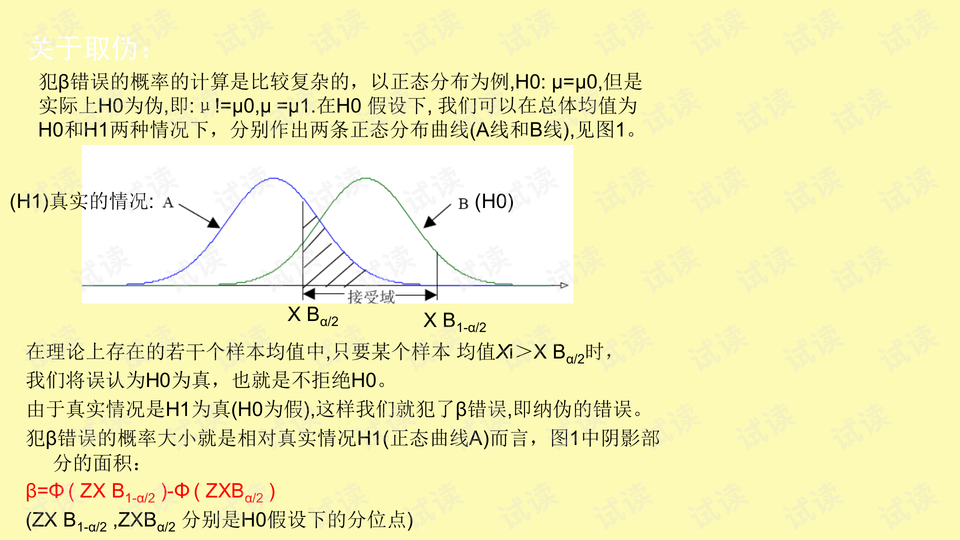
第一类错误（Type I error），在统计学中是指错误地拒绝了一个真实的零假设（null hypothesis）。假设检验中的零假设通常是我们想要验证的假设，如果零假设为真而我们错误地拒绝了它，便发生了第一类错误。犯第一类错误的概率通常用α表示，α的大小反映了我们进行假设检验时对犯这种错误的容忍度。

在实际应用中，α的取值范围通常在0到1之间。当α=0时，意味着我们完全不允许犯第一类错误，但这会导致我们很难拒绝零假设，因此可能会频繁犯第二类错误（Type II error）。反之，当α取值较大时，虽然拒绝零假设变得更加容易，但犯第一类错误的可能性也会增加。在研究和实践中，常用的α值有0.05、0.01和0.10，其中0.05是最常用的显著性水平。

### 2.1.2 第一类错误在实际中的案例分析

在药物临床试验中，第一类错误可能会导致错误地认为一个没有效果的药物是有效的，从而推向市场。例如，假定有一个新药，实际上它并没有比现有药物更好的疗效，但由于样本量不足或数据变异较大，临床试验结果错误地表明新药更有效。当该药物被广泛使用时，不仅浪费了医疗资源，还可能给患者带来不必要的风险。

在产品质量控制中，第一类错误可能表现为错误地拒绝了一个实际上合格的产品批次。例如，工厂生产了一批电子元件，假设它们的平均寿命超过了规定的标准。由于抽样误差，一个不合格的产品批次可能错误地被认定为合格，这可能导致更多的不合格产品流入市场，给消费者带来损失。

## 2.2 第一类错误的控制方法

### 2.2.1 设置合适的显著性水平

为了控制第一类错误，我们需要合理设置显著性水平α。这个过程涉及到对研究问题的理解、对潜在风险的评估以及对错误成本的认识。在决定α值时，通常需要考虑以下几个因素：

1. **研究领域与常规**：不同的学科有不同的习惯，例如在心理学研究中，α=0.05被广泛接受；而在物理学中，α值可能会更小。
2. **风险偏好**：研究者对错误的容忍度不同，例如在涉及人类健康的重要研究中，研究者可能更倾向于设置较低的α值以降低风险。
3. **后果的严重性**：错误的后果越严重，选择的α值应该越低。在错误可能导致重大损失的情况下，应当考虑更加严格的显著性水平。

### 2.2.2 多重假设检验的校正策略

当进行多重假设检验时，单一的显著性水平设置可能不足以控制第一类错误的累积概率。例如，在对多个基因表达水平进行检验时，即使每个检验的α值设定为0.05，但当检验次数足够多时，至少有一个错误拒绝零假设的概率会显著增加。为了解决这一问题，研究者经常采用多重假设检验的校正策略，包括：

1. **Bonferroni校正**：该方法简单，它将α值除以检验次数。例如，如果有10次独立的检验，α值会被调整为0.05/10=0.005。
2. **Benjamini-Hochberg程序**：这是一种更灵活的控制错误发现率（FDR）的方法。它根据每个假设检验的P值排序，控制总的错误发现率，允许部分错误的发生，但不会过多。
3. **Holm方法**：这一方法在Bonferroni校正的基础上稍作改进，它考虑了检验之间的相关性，并且在实践中通常比Bonferroni校正提供更高的统计功效。

graph TD
    A[开始多重假设检验校正] --> B{选择校正方法}
    B -->|Bonferroni校正| C[计算修正后的显著性水平]
    B -->|Benjamini-Hochberg程序| D[控制FDR]
    B -->|Holm方法| E[考虑检验顺序和相关性]
    C --> F[进行每个假设检验]