多变量数据的假设检验：多元方差分析与多变量t检验的实战应用

# 1. 多变量数据假设检验概述

在进行科学实验或统计研究时，我们经常需要对数据做出假设，并检验这些假设以得出结论。多变量数据假设检验是统计学中的一个重要分支，它涉及到两个或多个随机变量，并对这些变量的整体分布特征进行假设检验。它通常用于研究多个观测变量与多个分组变量之间的关系。多变量数据假设检验能够帮助我们解答诸如不同处理条件或组别对多个观测变量是否有显著影响的问题，以及各组间是否存在着显著的差异。

多变量数据假设检验的一个典型应用是多元方差分析（MANOVA），它不仅考虑了单一变量的均值差异，还能同时考虑多个变量组合的均值差异，提高了实验设计的效率和结果的解释能力。在本章中，我们将对多变量数据假设检验的基本概念和应用进行概述，为理解后续章节中的多元方差分析和多变量t检验奠定基础。

# 2. 多元方差分析（MANOVA）理论基础

### 2.1 方差分析的基本原理

#### 2.1.1 单变量方差分析(ANOVA)回顾

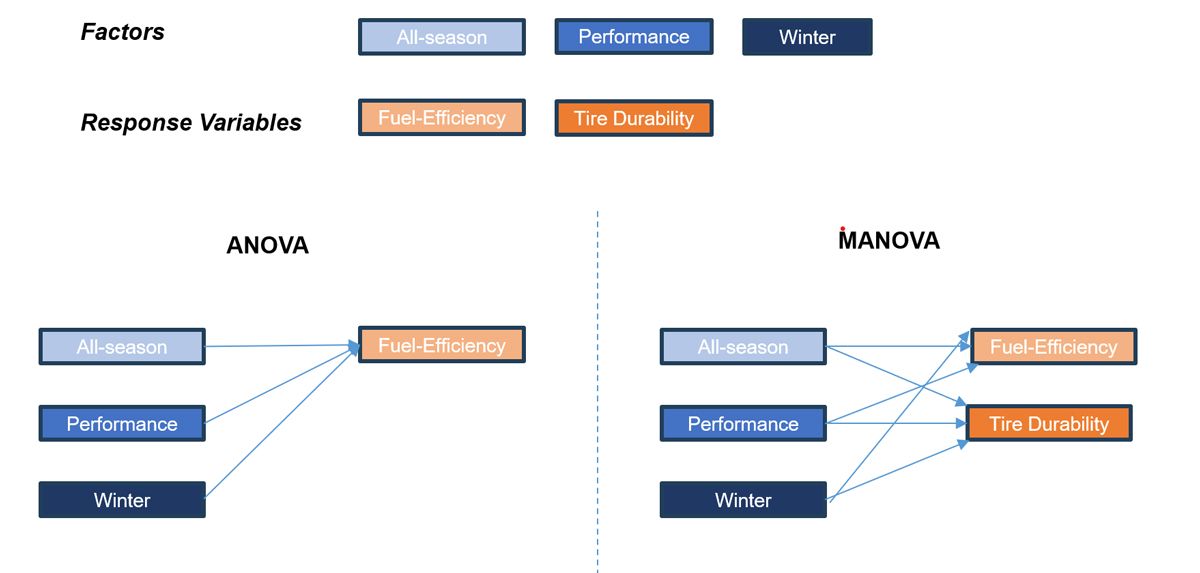
单变量方差分析（ANOVA）是统计学中用于检验三个或以上样本均值是否存在显著差异的方法。在ANOVA中，我们通常检验如下假设：

- 零假设（H0）：所有组的均值相等。
- 备择假设（H1）：至少有一组均值与其他组不同。

ANOVA 的核心是将总变异分解为组间变异和组内变异。组间变异衡量的是各组均值之间的差异，而组内变异衡量的是组内数据点与组均值之间的差异。通过计算 F 统计量，我们可以判断组间变异是否显著大于组内变异，从而决定是否拒绝零假设。

##### 代码块示例

import statsmodels.api as sm
from statsmodels.formula.api import ols

# 示例数据
data = sm.datasets.get_rdataset('ToothGrowth', 'datasets').data

# 构建模型
model = ols('len ~ C(dose)', data=data).fit()

# 执行ANOVA
anova_results = sm.stats.anova_lm(model, typ=2)
print(anova_results)

以上代码使用了`statsmodels`库来执行ANOVA，并且将结果输出到控制台。`typ=2`表示使用第二类平方和进行计算。这些步骤展示了ANOVA分析的直接应用，可以推广到多元方差分析。

#### 2.1.2 多元方差分析的统计模型

多元方差分析（MANOVA）是ANOVA在多维情况下的扩展，它允许我们同时分析多个响应变量。在MANOVA中，我们不再只关注一个因变量的均值差异，而是关注多个因变量共同作用下的组间差异。MANOVA使用Wilk's Lambda统计量、Pillai's Trace、Hotelling-Lawley Trace或Roy's Largest Root等统计方法来测量组间和组内变异的差异。

### 2.2 多元方差分析的前提条件

#### 2.2.1 数据分布的正态性

正态性是进行多元方差分析的一个基本假设，意味着所有因变量在每个组中都应该接近正态分布。在实际应用中，可以通过绘制Q-Q图或进行Shapiro-Wilk检验来评估数据的正态性。

##### 代码块示例

import scipy.stats as stats

# Shapiro-Wilk检验函数
def shapiro_test(dataframe):
    results = []
    for column in dataframe:
        stat, p = stats.shapiro(dataframe[column])
        results.append([column, stat, p])
    return results

# 示例数据
data = sm.datasets.get_rdataset('ToothGrowth', 'datasets').data
shapiro_results = shapiro_test(data[['len', 'supp']]) # 只测试len和supp列
print(shapiro_results)

此代码块定义了一个函数`shapiro_test`来执行Shapiro-Wilk检验。它接受一个数据框架作为输入，并返回每个列的Shapiro-Wilk统计量和P值。

#### 2.2.2 各组方差-协方差矩阵的等同性

MANOVA对各组数据的方差-协方差矩阵的等同性有要求，这通常通过Box's M检验来评估。若检验统计量显著，则违反了方差-协方差矩阵等同性的假设。

##### 代码块示例

from pingouin import multivariate_normality

# Pingouin库中的Box's M检验
boxm_results = multivariate_normality(data[['len', 'supp']], alpha=0.05)
print(boxm_results)

这里，我们使用了`pingouin`库中的`multivariate_normality`函数来测试数据是否满足方差-协方差矩阵的等同性假设。

#### 2.2.3 观测独立性

观测独立性意味着每个观测数据点都是独立的，不应受到其他数据点的影响。在一些试验设计中，如纵向研究，这一假设可能不成立，此时需要进行重复测量的方差分析或混合模型分析。

### 2.3 多元方差分析的实施步骤

#### 2.3.1 假设的构建

在MANOVA中，我们构建的假设如下：

- 零假设（H0）：所有组的均值向量相等。
- 备择假设（H1）：至少有一个组的均值向量与其他组不同。

#### 2.3.2 检验统计量的计算

MANOVA的检验统计量有多种，如Wilk's Lambda、Pillai's Trace、Hotelling-Lawley Trace或Roy's Largest Root。选择哪一种取决于数据的特性以及研究者的需求。

##### 代码块示例

from statsmodels.multivariate.manova import MANOVA

# 构建MANOVA模型
manova_model = MANOVA.from_formula('len + supp ~ C(dose)', data=data)

# 进行MANOVA
manova_results = manova_model.mv_test()
print(manova_results)

在本代码块中，我们使用了`statsmodels`库来执行MANOVA。`mv_test`方法返回了一个包含各种检验统计量的对象，允许我们检验不同组间均值向量的差异。

#### 2.3.3 结果的解释与决策

MANOVA的结果提供了多个检验统计量和相应的P值，帮助我们判断组间均值向量是否存在显著差异。如果P值小于设定的显著性水平（如0.05），则拒绝零假设，认为至少有一组均值与其他组有显著差异。

### 结论

多元方差分析是一种强有力的统计工具，它扩展了单变量方差分析，允许我们同时考虑多个因变量的差异。它依赖于若干关键的前提假设，如数据的正态分布、组间方差-协方差矩阵的等同性和观测的独立性。在应用MANOVA时，我们必须先检验这些假设，然后才能解释检验统计量并得出科学的结论。通过上述代码示例，我们可以看到如何使用Python进行数据的假设检验和MANOVA分析，以深入理解多变量数据的结构。

# 3. 多变量t检验（Hotelling's T-squared）理论框架

在多变量数据统计分析中，多变量t检验是评估两个或更多个多元数据组均值差异的常用方法。在多元分析中，多变量t检验通常用来替代单变量t检验，尤其是当研究设计涉及多个相关响应变量时。本章旨在详细介绍多变量t检验的概念、应用、统计假设以及计算方法，通过理论与实例相结合的方式，为读者提供深入理解和应用多变量t检验的全面视角。

## 3.1 多变量t检验的概念与应用

### 3.1.1 单样本t检验与多变量t检验的比较

在统计学中，单样本t检验是用于比较单个样本均值与已知总体均值的统计检验方法。而多变量t检验（Hotelling's T-squared test）扩展了这一概念，使得多个