高级应用：探索DeepAR时间序列预测模型的无限潜力，解锁预测新境界

# 1. 时间序列预测简介

时间序列预测是预测未来值的一门技术，它利用历史数据来建立模型，从而对未来事件进行预测。时间序列预测在各个领域都有着广泛的应用，例如：

- **金融：**预测股票价格、汇率和商品价格
- **零售：**预测需求、库存和销售
- **制造业：**预测机器故障和生产率
- **医疗保健：**预测疾病爆发、患者预后和治疗效果

时间序列预测模型有多种类型，其中一种流行的方法是深度学习模型，例如 DeepAR 模型。DeepAR 模型是一种强大的时间序列预测模型，它利用深度学习技术来捕获时间序列数据的复杂模式。

# 2. DeepAR模型的理论基础

### 2.1 时间序列的数学建模

时间序列是一种按时间顺序排列的数据序列，它可以用来描述随时间变化的现象。时间序列建模是通过数学模型来捕捉时间序列中的模式和趋势，以便进行预测和分析。

#### 自回归模型（AR）

自回归模型（AR）是一种最简单的线性时间序列模型，它假设当前时间点的观测值只与过去几个时间点的观测值相关。AR模型的数学表达式为：

y_t = c + ∑(i=1)^p φ_i * y_(t-i) + ε_t

其中：

* y_t 为当前时间点的观测值
* c 为常数项
* φ_i 为自回归系数
* p 为自回归阶数
* ε_t 为误差项

#### 滑动平均模型（MA）

滑动平均模型（MA）假设当前时间点的观测值只与过去几个时间点的误差项相关。MA模型的数学表达式为：

y_t = μ + ∑(i=1)^q θ_i * ε_(t-i) + ε_t

其中：

* μ 为均值
* θ_i 为滑动平均系数
* q 为滑动平均阶数
* ε_t 为误差项

#### 自回归滑动平均模型（ARMA）

自回归滑动平均模型（ARMA）结合了AR和MA模型，它假设当前时间点的观测值与过去几个时间点的观测值和误差项相关。ARMA模型的数学表达式为：

y_t = c + ∑(i=1)^p φ_i * y_(t-i) + ∑(i=1)^q θ_i * ε_(t-i) + ε_t

### 2.2 DeepAR模型的架构和算法

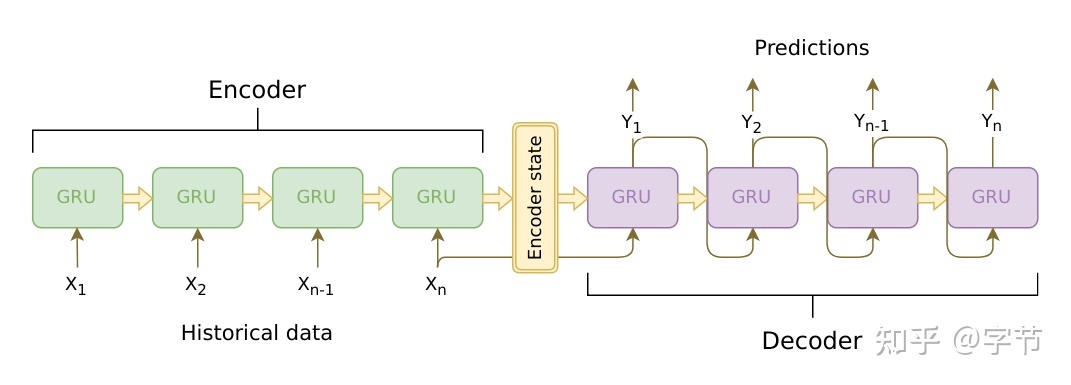
DeepAR模型是一种深度学习时间序列预测模型，它基于编码器-解码器架构。编码器负责将输入时间序列编码成固定长度的向量，解码器负责将编码后的向量解码成预测值。

#### 编码器

DeepAR模型的编码器是一个卷积神经网络（CNN），它由多个卷积层和池化层组成。CNN能够提取时间序列中的局部模式和趋势。

#### 解码器

DeepAR模型的解码器是一个循环神经网络（RNN），它由多个LSTM层组成。LSTM能够处理长序列数据，并捕捉时间序列中的长期依赖关系。

#### 训练算法

DeepAR模型使用最大似然估计（MLE）算法进行训练。MLE算法的目标是找到一组模型参数，使模型对给定数据集的似然函数最大化。

#### 预测算法

训练好的DeepAR模型可以用于预测未来时间点的观测值。预测算法通过将输入时间序列编码成固定长度的向量，然后将向量解码成预测值来进行。

# 3. DeepAR模型的实践应用

##