MATLAB滤波器实战宝典：揭秘滤波类型、参数和实现，助你解决信号处理难题

# 1. MATLAB滤波器概述

MATLAB滤波器是一组用于处理和分析数据的强大工具。它们允许工程师和科学家从信号中去除噪声、提取特征并增强信号。MATLAB提供了一个全面的滤波器工具箱，其中包含各种滤波器类型，包括时域和频域滤波器。

时域滤波器直接操作信号的时间序列，而频域滤波器则在信号的频率域中进行操作。时域滤波器的常见类型包括移动平均滤波器和指数加权移动平均滤波器，而频域滤波器的常见类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。

# 2. 滤波器理论与分类

### 2.1 时域滤波器

时域滤波器直接对时域信号进行处理，其输出与当前时刻及过去时刻的输入信号有关。时域滤波器主要分为以下两类：

#### 2.1.1 移动平均滤波器

移动平均滤波器（Moving Average Filter，简称 MA）通过对信号窗口内的数据进行平均来平滑信号。其数学表达式为：

y[n] = (1/N) * Σ[x[n-i], i = 0, ..., N-1]

其中：

* `y[n]` 为滤波后的输出信号
* `x[n]` 为输入信号
* `N` 为窗口大小

移动平均滤波器具有平滑噪声和保留信号低频分量的特点，但会引入时延。

#### 2.1.2 指数加权移动平均滤波器

指数加权移动平均滤波器（Exponential Weighted Moving Average Filter，简称 EWMA）是对移动平均滤波器的改进，其权重随着时间的推移呈指数衰减。其数学表达式为：

y[n] = α * x[n] + (1 - α) * y[n-1]

其中：

* `α` 为平滑系数，范围为 (0, 1)
* `y[n]` 为滤波后的输出信号
* `x[n]` 为输入信号
* `y[n-1]` 为上一次滤波后的输出信号

指数加权移动平均滤波器比移动平均滤波器更能快速响应信号变化，但对噪声的平滑效果较差。

### 2.2 频域滤波器

频域滤波器通过对信号的傅里叶变换进行处理，其输出与信号的频率分量有关。频域滤波器主要分为以下四类：

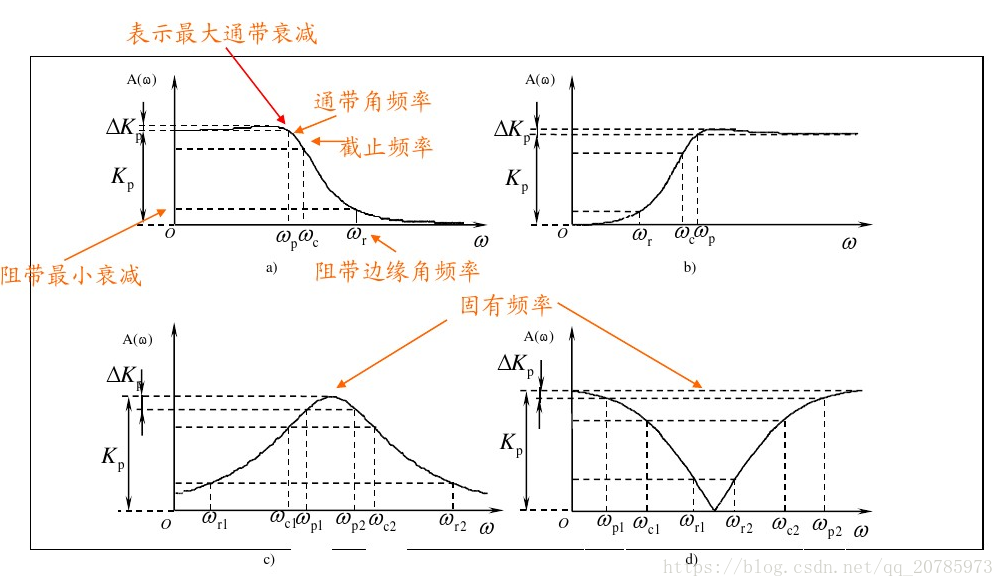
#### 2.2.1 低通滤波器

低通滤波器（Low-Pass Filter，简称 LPF）允许低频分量通过，而衰减高频分量。其频率响应曲线如下图所示：

[图片：低通滤波器频率响应曲线]

#### 2.2.2 高通滤波器

高通滤波器（High-Pass Filter，简称 HPF）允许高频分量通过，而衰减低频分量。其频率响应曲线如下图所示：

[图片：高通滤波器频率响应曲线]

#### 2.2.3 带通滤波器

带通滤波器（Band-Pass Filter，简称 BPF）允许特定频带内的分量通过，而衰减其他频带的分量。其频率响应曲线如下图所示：

[图片：带通滤波器频率响应曲线]

#### 2.2.4 带阻滤波器

带阻滤波器（Band-Stop Filter，简称 BSF）允许特定频带外的分量通过，而衰减该频带内的分量。其频率响应曲线如下图所示：

[图片：带阻滤波器频率响应曲线]

频域滤波器具有选择性好、时延小等优点，但对噪声的平滑效果较差。

# 3. MATLAB滤波器设计与实现

### 3.1 FIR滤波器设计

#### 3.1.1 窗函数法

窗函数法是一种常用的FIR滤波器设计方法，其基本思想是将理想滤波器的频率响应与一个窗函数相乘，从而得到一个实际可实现的滤波器。常用的窗函数有矩形窗、汉明窗、海宁窗等。

**代码块：**

% 设计一个截止频率为0.5的低通FIR滤波器，使用矩形窗
order = 100; % 滤波器阶数
cutoff_freq = 0.5; % 截止频率
window = rectwin(order + 1); % 矩形窗
h = fir1(order, cutoff_freq, window); % 设计滤波器

% 绘制滤波器的频率响应
freqz(h, 1, 512);
title('FIR低通滤波器（矩形窗）的频率响应');

**逻辑分析：**

* `fir1`函数用于设计FIR滤波器，其参数包括滤波器阶数、截止频率和窗函数。
* `rectwin`函数生成一个矩形窗，其参数为窗的长度。
* `freqz`函数绘制滤波器的频率响应，其参数包括滤波器的传递函数、单位采样频率和频率点数。

#### 3.1.2 最小二乘法

最小二乘法是一种优化方法，可以用于设计FIR滤波器。其基本思想是找到一组滤波器系数，使得滤波器的频率响应与理想频率响应之间的误差最小。

**代码块：**

% 设计一个截止频率为0.5的低通FIR滤波器，使用最小二乘法
order = 100; % 滤波器阶数
cutoff_freq = 0.5; % 截止频率
h = firpm(order, [0 cutoff_freq 1], [1 1 0]); % 设计滤波器

% 绘制滤波器的频率响应
freqz(h, 1, 512);
title('FIR低通滤波器（最小二乘法）的频率响应');

**逻辑分析：**

* `firpm`函数用于设计FIR滤波器，其参数包括滤波器阶数、频带边缘和频带增益。
* `[0 cutoff_freq 1]`指定了滤波器的频带边缘，`[1 1 0]`指定了滤波器的频带增益。

### 3.2 IIR滤波器设计

#### 3.2.1 巴特沃斯滤波器

巴特沃斯滤波器是一种IIR滤波器，其频率响应在截止频率附近具有平坦的通带和陡峭的阻带。

**代码块：**

% 设计一个截止频率为0.5的低通巴特沃斯滤波器
order = 5; % 滤波器阶数
cutoff_freq = 0.5; % 截止频率
[b, a] = butter(order, cutoff_freq); % 设计滤波器

% 绘制滤波器的频率响应
freqz(b, a, 512);
title('巴特沃斯低通滤波器的频率响应');

**逻辑分析：**

* `butter`函数用于设计巴特沃斯滤波器，其参数包括滤波器阶数和截止频率。
* `[b, a]`分别表示滤波器的分子和分母系数。

#### 3.2.2 切比雪夫滤波器

切比雪夫滤波器是一种IIR滤波器，其频率响应在通带内具有等纹波，在阻带内具有陡峭的衰减。

**代码块：**

% 设计一个截止频率为0.5的低通切比雪夫滤波器
order = 5; % 滤波器阶数
cutoff_freq = 0.5; % 截止频率
ripple = 0.1; % 通带纹波
[b, a] = cheby1(order, ripple, cutoff_freq); % 设计滤波器

% 绘制滤波器的频率响应
freqz(b, a, 512);
title('切比雪夫低通滤波器的频率响应');

**逻辑分析：**

* `cheby1`函数用于设计切比雪夫滤波器，其参数包括滤波器阶数、通带纹波和截止频率。
* `[b, a]`分别表示滤波器的分子和分母系数。

### 3.3 滤波器参数优化

#### 3.3.1 滤波器阶数

滤波器阶数是影响滤波器性能的一个重要参数。阶数越高，滤波器的截止频率越陡峭，但计算量也越大。

#### 3.3.2 截止频率

截止频率是滤波器将信号分为通带和阻带的频率。截止频率越高，通带的带宽越大，但阻带的衰减也越小。

**表格：**

| 参数 | 影响 |
|---|---|
| 滤波器阶数 | 截止频率的陡峭度、计算量 |
| 截止频率 | 通带的带宽、阻带的衰减 |

**mermaid格式流程图：**

graph LR
subgraph 滤波器阶数
    A[滤波器阶数] --> B[截止频率的陡峭度]
    A[滤波器阶数] --> C[计算量]
end
subgraph 截止频率
    D[截止频率] --> E[通带的带宽]
    D[截止频率] --> F[阻带的衰减]
end

# 4. MATLAB滤波器应用实例

### 4.1 图像滤波

#### 4.1.1 去噪滤波

**应用场景：**图像去噪是图像处理中的一个基本任务，旨在去除图像中的噪声，例如高斯噪声、椒盐噪声等。MATLAB提供了多种滤波器函数来实现图像去噪，例如`imnoise`、`imfilter`和`wiener2`。

**操作步骤：**

1. 读取原始图像：`I = imread('image.jpg');`
2. 添加噪声：`I_noise = imnoise(I, 'gaussian', 0.05);`
3. 应用去噪滤波：`I_denoised = wiener2(I_noise, [5 5]);`
4. 显示去噪后的图像：`imshow(I_denoised);`

**代码块：**

% 读取原始图像
I = imread('image.jpg');

% 添加高斯噪声
I_noise = imnoise(I, 'gaussian', 0.05);

% 应用维纳滤波去噪
I_denoised = wiener2(I_noise, [5 5]);

% 显示去噪后的图像
imshow(I_denoised);

**逻辑分析：**

* `imnoise`函数添加高斯噪声，参数`0.05`表示噪声标准差。
* `wiener2`函数使用维纳滤波去噪，参数`[5 5]`表示滤波器内核大小。
* `imshow`函数显示去噪后的图像。

#### 4.1.2 边缘检测

**应用场景：**边缘检测是图像处理中另一个重要任务，旨在检测图像中的边缘和轮廓。MATLAB提供了`edge`和`canny`等函数来实现边缘检测。

**操作步骤：**

1. 读取原始图像：`I = imread('image.jpg');`
2. 转换为灰度图像：`I_gray = rgb2gray(I);`
3. 应用边缘检测：`edges = edge(I_gray, 'canny');`
4. 显示边缘检测结果：`imshow(edges);`

**代码块：**

% 读取原始图像
I = imread('image.jpg');

% 转换为灰度图像
I_gray = rgb2gray(I);

% 应用Canny边缘检测
edges = edge(I_gray, 'canny');

% 显示边缘检测结果
imshow(edges);

**逻辑分析：**

* `rgb2gray`函数将彩色图像转换为灰度图像。
* `edge`函数使用Canny边缘检测算法检测边缘，参数`'canny'`表示使用Canny算法。
* `imshow`函数显示边缘检测结果。

### 4.2 信号滤波

#### 4.2.1 去除噪声

**应用场景：**信号去噪是信号处理中的一个常见任务，旨在去除信号中的噪声，例如高频噪声、低频噪声等。MATLAB提供了`filter`和`smooth`等函数来实现信号去噪。

**操作步骤：**

1. 加载信号数据：`data = load('signal.mat');`
2. 添加噪声：`data_noise = data.signal + 0.1 * randn(size(data.signal));`
3. 应用滤波去噪：`data_denoised = filter(b, a, data_noise);`
4. 绘制去噪后的信号：`plot(data_denoised);`

**代码块：**

% 加载信号数据
data = load('signal.mat');

% 添加高斯噪声
data_noise = data.signal + 0.1 * randn(size(data.signal));

% 设计低通滤波器
b = fir1(10, 0.5);
a = 1;

% 应用滤波去噪
data_denoised = filter(b, a, data_noise);

% 绘制去噪后的信号
plot(data_denoised);

**逻辑分析：**

* `randn`函数生成高斯噪声。
* `fir1`函数设计低通滤波器，参数`10`表示滤波器阶数，`0.5`表示截止频率。
* `filter`函数应用滤波器去噪，参数`b`和`a`分别表示滤波器的分子和分母多项式。
* `plot`函数绘制去噪后的信号。

#### 4.2.2 提取特征

**应用场景：**信号特征提取是信号处理中的另一个重要任务，旨在从信号中提取有价值的特征，用于模式识别、分类等任务。MATLAB提供了`findpeaks`和`spectrogram`等函数来实现信号特征提取。

**操作步骤：**

1. 加载信号数据：`data = load('signal.mat');`
2. 查找峰值：`[pks, locs] = findpeaks(data.signal);`
3. 计算频谱：`[S, F, T] = spectrogram(data.signal);`
4. 绘制频谱图：`imagesc(T, F, 20 * log10(abs(S)));`

**代码块：**

% 加载信号数据
data = load('signal.mat');

% 查找峰值
[pks, locs] = findpeaks(data.signal);

% 计算频谱
[S, F, T] = spectrogram(data.signal);

% 绘制频谱图
imagesc(T, F, 20 * log10(abs(S)));

**逻辑分析：**

* `findpeaks`函数查找信号中的峰值，返回峰值幅度和位置。
* `spectrogram`函数计算信号的频谱，返回频谱图、频率和时间。
* `imagesc`函数绘制频谱图，参数`20 * log10(abs(S))`表示以分贝为单位绘制频谱。

# 5.1 多级滤波

多级滤波是一种通过将多个滤波器串联或并行连接来实现更复杂滤波功能的技术。

### 5.1.1 级联滤波器

级联滤波器将多个滤波器串联连接，每个滤波器的输出作为下一个滤波器的输入。这种结构可以实现更复杂的滤波特性，例如：

% 创建一个低通滤波器和一个高通滤波器
lowpass = designfilt('lowpassfir', 'PassbandFrequency', 100, 'StopbandFrequency', 200, 'FilterOrder', 10);
highpass = designfilt('highpassfir', 'PassbandFrequency', 200, 'StopbandFrequency', 100, 'FilterOrder', 10);

% 将两个滤波器级联
cascadeFilter = cascade(lowpass, highpass);

% 应用级联滤波器
filteredSignal = filter(cascadeFilter, signal);

### 5.1.2 并行滤波器

并行滤波器将多个滤波器并行连接，每个滤波器处理输入信号的不同部分。这种结构可以实现同时进行多种滤波操作，例如：

% 创建一个低通滤波器和一个高通滤波器
lowpass = designfilt('lowpassfir', 'PassbandFrequency', 100, 'StopbandFrequency', 200, 'FilterOrder', 10);
highpass = designfilt('highpassfir', 'PassbandFrequency', 200, 'StopbandFrequency', 100, 'FilterOrder', 10);

% 将两个滤波器并行连接
parallelFilter = parallel(lowpass, highpass);

% 应用并行滤波器
[lowpassOutput, highpassOutput] = filter(parallelFilter, signal);