山东大学ACM模板：涵盖数论、分数规划与经典问题详解

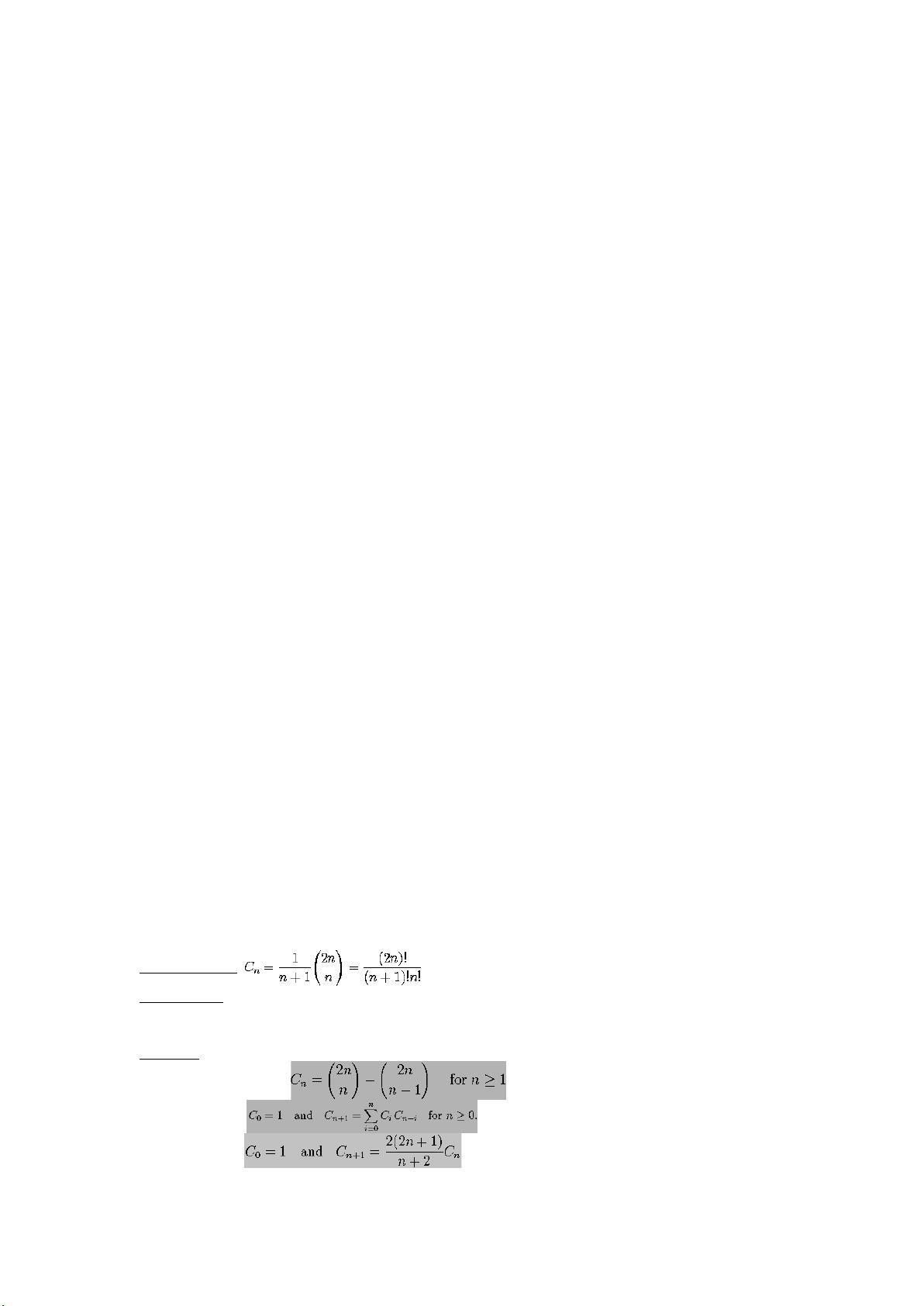
山东大学ACM模板-杂题是一份精心整理的资源，旨在帮助学生解决在ACM国际大学生程序设计竞赛中可能遇到的各种数学、算法和数据结构问题。这份模板涵盖了广泛的主题，包括但不限于： 1. **数论基础**：涉及最大公约数、扩展欧几里得算法、中国余数定理（处理模线性方程组）、逆元计算、同余方程合并等，这些都是解决许多算法问题的基础。 2. **数列与特殊函数**：如斯特林数的改进版、第二类斯特灵数的奇偶校验、卡特兰数、泰勒级数、麦克劳林级数等，这些用于计算和计数问题。 3. **递推关系**：包括2阶和K阶线性齐次及非齐次递推关系，这对于解决组合优化问题非常关键，如整数划分、Fibonacci数列等。 4. **组合数学**：有重复排列/组合的总结、指数型母函数，以及计数问题的解决方案。 5. **数值与统计**：自然数的数字统计，以及递推关系的线性代数证明。 6. **概率与图论**：如最大密度子图、最优比率问题（如MST、环形结构）和Steiner树问题。 7. **搜索与匹配**：KMP算法、子数组查询（RMQ）、最长上升/不降子序列、逆序对、sigma[n]的计算等。 8. **排序与计数**：基数排序、枚举子集、区间最大频率、稳定婚姻问题等。 9. **特殊操作**：如异或最大值、字典序全排列（互转）、历法算法、位运算（如位移、位与、位或等）以及Int64操作。 10. **特定问题与工具**：如素数生成器、反素数表、Josephus问题、皇后问题（使用位运算）、DeBruijn序列等。 11. **优化方法**：如分数规划中的Dinkelbach算法、裸分规问题，以及与最大密度子图相关的最优比率算法。 12. **字符串处理**：如KMP算法，以及与字符串相关的问题如寻找两个数异或的最大值和字典序全排列。 13. **实用辅助**：如Calendar类库总结，以及数学公式引用。 这份模板不仅提供了解决问题的具体算法，还包括了对概念的理解和应用，是参加ACM竞赛的学生和研究者不可或缺的学习参考资料。