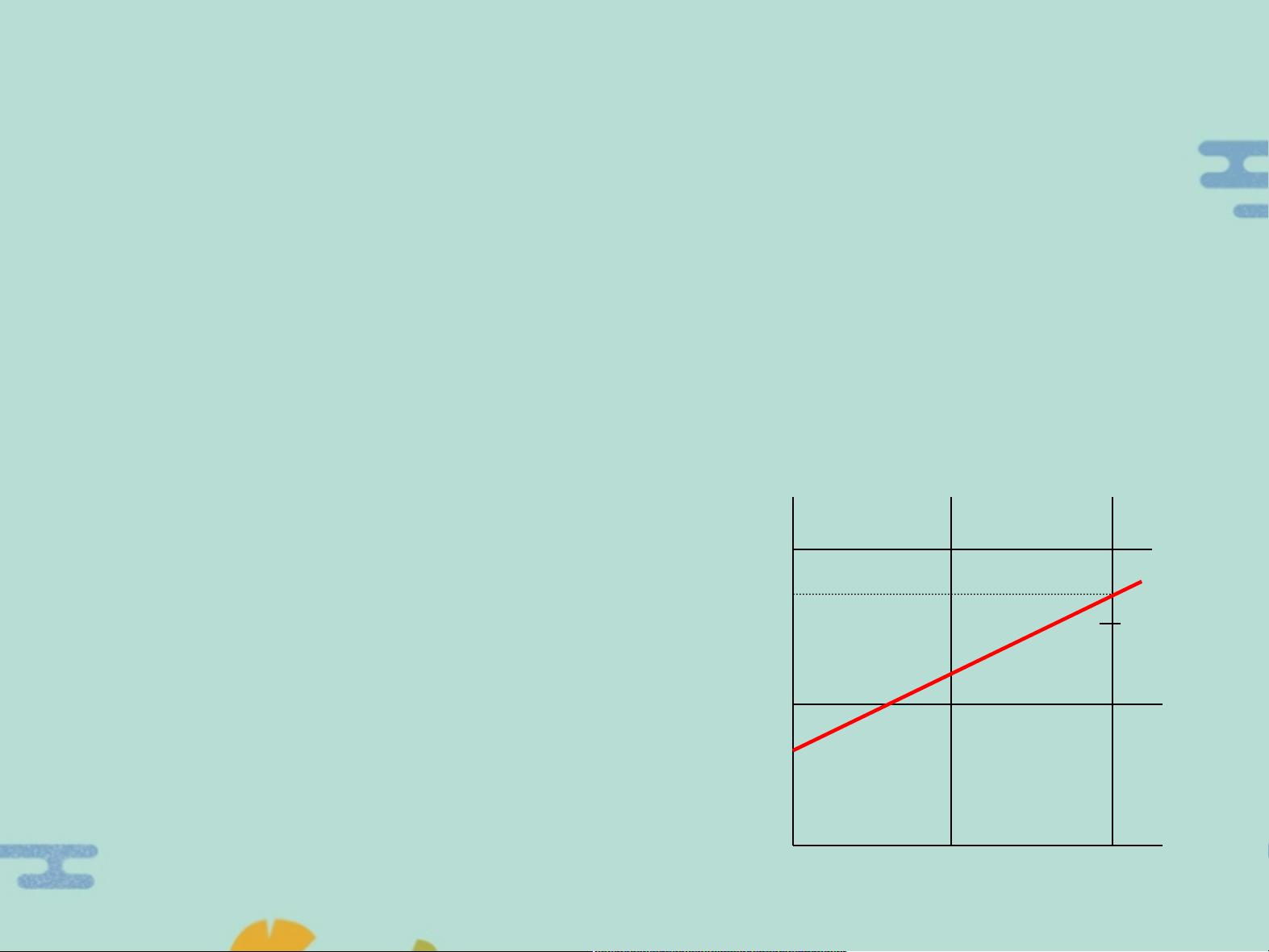计算机图形学概论：直线生成的DDA算法 - 用离散网格点表示直线

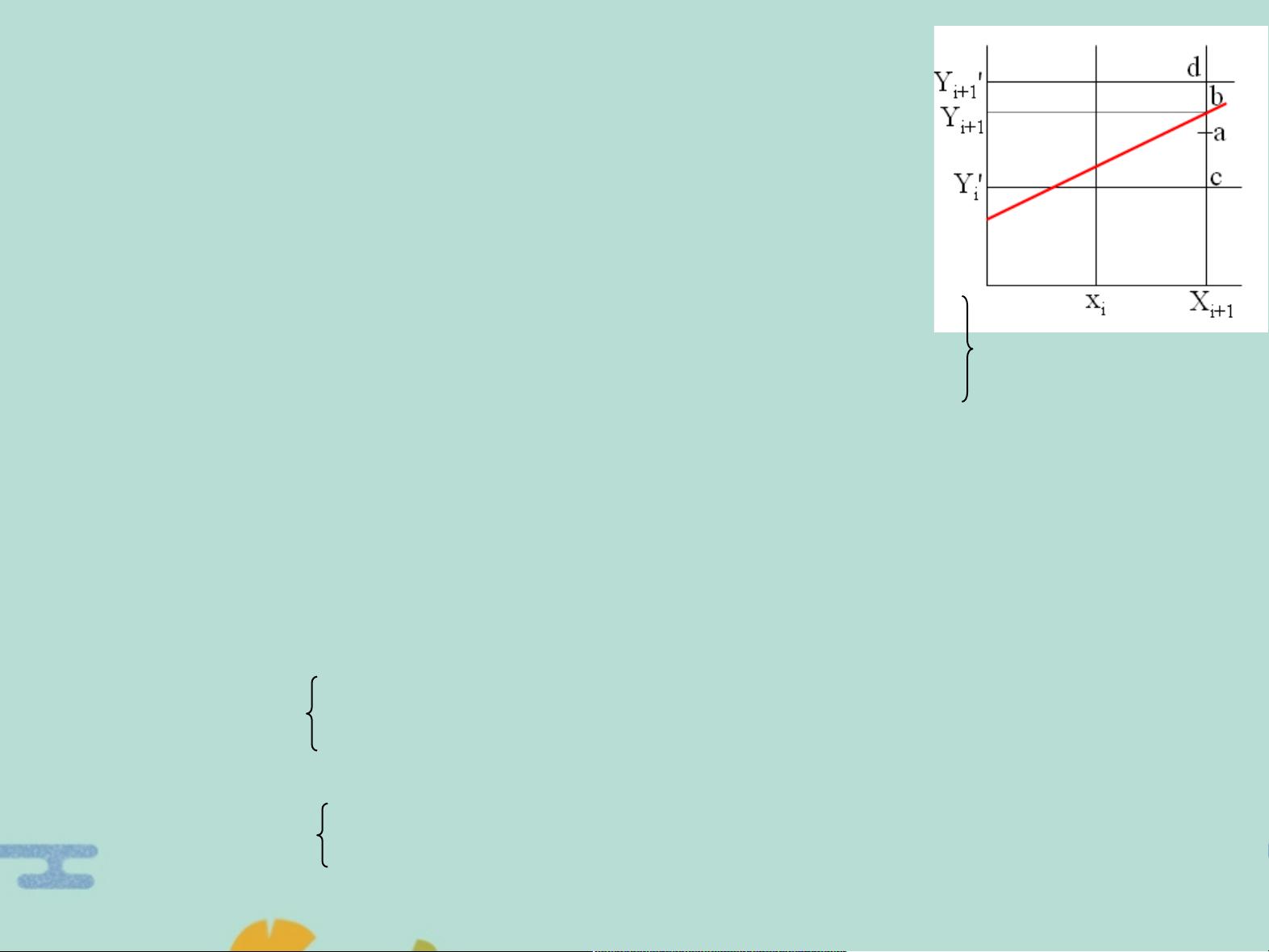
本文主要介绍了计算机图形学概论中关于二维图形生成技术的内容。其中第三章讨论了直线图形的生成，首先介绍了生成直线的数字差分分析(DDA)算法。无论是光栅扫描显示器还是绘图机，都可以看成有一个网格存在，对显示器来说每一个像素就是一个网格点，对绘图机来说笔每走一步的终点也可以看成是一个网格的结点。在光栅扫描显示器上表示一条直线，就是要用最靠近直线的一些网格点来代表这一直线。这个网格构成屏幕和绘图机纸张的一个坐标系，相邻两个网点的距离取为1，每个网格点的坐标均取整数。假设直线的起点坐标为P1 (x1,y1)，终点坐标为P2 (x2,y2)，则可以根据△x和△y的增量以及直线的斜率来求得直线P1P2和y方向网格线的交点，从而用象素点(图中的网格结点)来表示。 接着，文档介绍了直线的中点画线算法。直线的中点画线算法是八分之一法则来进行计算的，其基本思想是从左下到右上，沿直线路径逐象素点递增。文档对中点画线算法进行了详细的数学推导和实例展示，说明了该算法的具体实现步骤和计算方法。 在介绍完直线的生成算法后，文档还讨论了直线段的裁剪问题。在实际的计算机图形学中，经常会遇到需要对直线段进行裁剪的情况。文档介绍了直线段裁剪的基本概念、裁剪算法和实例演示，包括了Cohen-Sutherland裁剪算法、Liang-Barsky裁剪算法等，对这些算法的原理和具体实现进行了详细的讲解。 除了直线图形的生成技术，文档还介绍了圆弧与椭圆的生成算法。对于圆弧与椭圆的生成，文档分别介绍了中点画圆弧算法和中点画椭圆算法，并通过实例演示展示了算法的具体实现过程和计算原理。 总的来说，本文介绍了计算机图形学概论中关于二维图形生成技术的相关内容，包括了直线图形的生成算法和直线段的裁剪问题，以及圆弧与椭圆的生成算法。通过详细的数学推导、算法原理讲解和实例演示，使读者能够全面了解和掌握这些二维图形生成技术，为进一步深入学习计算机图形学打下扎实的基础。