几何中线屈服方程：Tresca与双剪应力轨迹间的创新

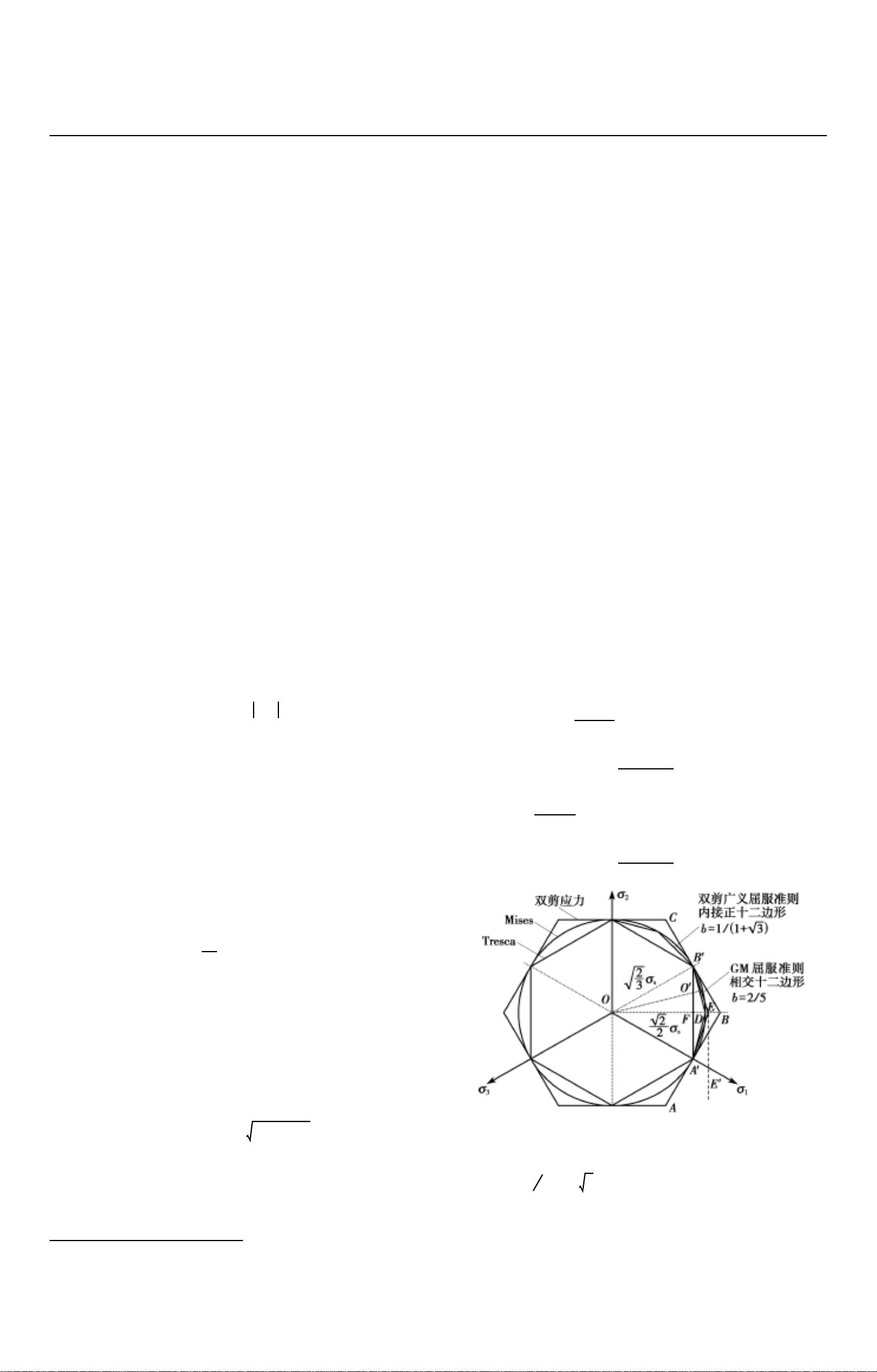
"由Tresca和双剪应力两轨迹间误差三角形中线确定的屈服方程 (2004年)" 这篇论文探讨了一种新的材料屈服准则，称为“几何中线屈服方程”或简称为GM屈服准则。该准则的建立基于Tresca屈服准则和双剪应力屈服轨迹之间的误差三角形的几何中线。在π平面（即主应力平面）上，Tresca屈服轨迹和双剪应力屈服轨迹形成一个误差三角形，研究者通过选取这个三角形的中线来定义新的屈服轨迹。 Tresca屈服准则，也称为最大剪切应力理论，指出材料屈服发生在两个最大正应力之差等于材料的屈服应力（σs）时。而双剪应力准则，是俞茂宏提出的，它考虑了最大剪切应力和平均剪切应力，当任一条件满足时，材料也会发生屈服。 在Haigh Westergaard应力空间中，研究者建立了GM屈服准则的应力方程。这个新准则的一个关键特性是它的线性性质，这意味着在描述材料屈服行为时，它提供了简单且直观的数学表示。此外，GM准则的屈服轨迹表现为与Mises屈服轨迹相交的等边非等角十二边形，这与Mises准则（von Mises屈服准则）的圆形轨迹不同。 论文还证明了GM准则的单位塑性功率表达式，并对其对Mises圆的逼近精度进行了分析。结果显示，GM准则与Mises准则相比，最大误差不超过2.9%，平均误差仅为0.95%，优于MY（平均屈服）准则的逼近精度1%。这表明GM屈服准则在描述塑性变形时具有较高的精度。 此外，论文提到GM准则的单位体积塑性功率表达式也是线性的，这进一步简化了在实际工程应用中的计算。通过实例和精度分析，GM屈服准则被证实是一种有效且精确的描述材料屈服行为的方法，特别是在金属成形等领域的应用。 关键词涉及Tresca准则、双剪应力轨迹、误差三角形、几何中线、等边非等角十二边形以及线性屈服准则，这些都是构建和理解GM屈服准则的核心概念。该研究对于理解材料的塑性行为和改进工程设计的计算模型具有重要意义。