图形与游戏开发3D数学基础教程

3星 · 超过75%的资源需积分: 10 54 浏览量更新于2024-07-27 收藏 12.32MB PDF 举报

《3D数学基础：图形与游戏开发指南》（3D Math Primer for Graphics and Game Development）由Fletcher Dunn和Ian Parberry合著，于2002年出版。该书是专为图形设计师和游戏开发者量身打造的实用教程，深入浅出地介绍了3D数学在图形与游戏制作中的核心概念和技术。本书由Wordware Publishing, Inc.发行，旨在帮助读者掌握三维空间中的向量、矩阵、坐标系转换、投影、光照、纹理映射等基础知识，这些都是构建3D世界和创建沉浸式游戏体验的基础。书中首先在第一章“引言”中，作者会解释3D数学对于现代图形和游戏开发的重要性，以及为何对这些基本数学原理有深入理解至关重要。1.1节可能会探讨3D数学与传统2D图形的区别，以及如何通过3D数学拓展游戏设计的可能性。第二章到第四章可能会详细介绍向量和矩阵运算，包括向量的加减乘除、标量和向量的点积和叉积、以及矩阵的乘法和逆运算，这些都是3D空间变换和动画的关键。作者会通过实际例子展示这些概念如何应用于游戏物体的位置、旋转和缩放。第五章可能会讲解几何体建模和坐标系统，如笛卡尔坐标、极坐标和柱坐标，以及它们在游戏中的应用，比如场景构建和碰撞检测。接下来章节可能涉及投影技术，如透视投影和正交投影，这对于实现真实感的3D视图至关重要。光线追踪和阴影计算在游戏中的表现力是另一个重点，这会在第六章至第七章详细讨论，包括光源、光衰减、反射和折射等概念。同时，作者会介绍如何通过着色器实现这些效果，尤其是在GPU上进行高效的处理。第八章和第九章将深入讲解纹理映射，包括UV坐标、贴图过滤和纹理合成，这对于纹理丰富的游戏和材质处理非常重要。最后，第十章可能会总结全文，回顾主要的概念，并提供一些项目示例或实战练习，以帮助读者巩固所学知识并将其应用于实际项目中。《3D数学基础：图形与游戏开发指南》是一本实用性极强的参考资料，适合想要提升3D图形和游戏开发技能的专业人士，也适合对3D数学感兴趣但缺乏系统学习路径的学生和爱好者。通过阅读这本书，读者不仅能掌握必要的数学工具，还能更好地理解和创造复杂的3D世界。

1.3 What You Should Know Before Reading

This Book

The theory part of this book assumes a prior knowledge of basic algebra and geometry, such as:

Manipulating algebraic expressions

Algebraic laws, such as the associative and distributive laws

Functions and variables

Basic 2D Euclidian geometry

In addition, some prior exposure to trigonometry is useful, but not required. A brief review of

some key mathematical concepts is included in Appendix A.

For the practice part, you need to understand some basics of programming in C++:

Program flow control constructs

Functions and parameters

Object-oriented programming and class design

No specific compiler or target platform is assumed. No “advanced” C++ language features are

used. The few language features that you may be unfamiliar with, such as operator overloading

and reference arguments, will be explained as they are needed.

1.4 Overview

Chapter 1 is the introduction, which you have almost finished reading. Hopefully, it has

explained for whom this book is written and why we think you should read the rest of it.

Chapter 2 explains the Cartesian coordinate system in 2D and 3D and discusses how the Car

tesian coordinate system is used to locate points in space.

Chapter 3 discusses examples of coordinate spaces and how they are nested in a hierarchy.

Chapter 4 introduces vectors and explains the geometric and mathematical interpretations of

vectors.

Chapter 5 discusses mathematical operations on vectors and explains the geometric interpre

tation of each operation.

Chapter 6 provides a usable C++ 3D vector class.

Chapter 7 introduces matrices from a mathematical and geometric perspective and shows

how matrices can be used to perform linear transformations.

Chapter 8 discusses different types of linear transformations and their corresponding matri

ces in detail.

Chapter 9 covers a few more interesting and useful properties of matrices.

Chapter 10 discusses different techniques for representing orientation and angular displace

ment in 3D.

Chapter 1: Introduction

from 1596 to 1650. Descartes is not just famous for inventing Cartesian mathematics, which at the

time was a stunning unification of algebra and geometry. He is also well known for taking a pretty

good stab at answering the question “How do I know something is true?” This question has kept

generations of philosophers happily employed and does not necessarily involve dead sheep

(which will disturbingly be a central feature of the next section), unless you really want it to. Des

cartes rejected the answers proposed by the ancient Greeks, which are ethos (roughly, “because I

told you so”), pathos (“because it would be nice”), and logos (“because it makes sense”), and set

about figuring it out for himself with a pencil and paper.

2.1 1D Mathematics

You’re reading this book because you want to know about 3D mathematics, so you’re probably

wondering why we’re bothering to talk about 1D math. Well, there are a couple of issues about

number systems and counting that we would like to clear up before we get to 3D.

Natural numbers, often called counting numbers, were invented millennia ago, probably to keep

track of dead sheep. The concept of “one sheep” came easily (see Figure 2.1), then “two sheep”

and “three sheep,” but people very quickly became convinced that this was too much work. They

gave up counting at some point and invariably began using “many sheep.” Different cultures gave

up at different points, depending on their threshold of boredom. Eventually, civilization expanded

to the point where we could afford to have people sitting around thinking about numbers instead of

doing more survival-oriented tasks, such as killing sheep and eating them. These savvy thinkers

immortalized the concept of zero (no sheep), and while they didn’t get around to naming all of the

natural numbers, they figured out various systems whereby we could name them if we really

wanted to, using digits such as “1”, “2”, etc. (or if you were Roman, “M”, “X”, “I,” etc.). Mathe

matics was born.

6 Chapter 2: The Cartesian Coordinate System

Figure 2.1: One dead sheep

Figure 2.2: A number line for the natural

numbers

The habit of lining sheep up in a row so that they can easily be counted leads to the concept of

a number line, that is, a line with the numbers marked off at regular intervals, as in Figure 2.2. This

line can, in principle, go on for as long as we wish, but to avoid boredom we have stopped at five

sheep and put on an arrowhead to let you know that the line can continue. Clear thinkers can visu

alize it going off to infinity, but historical purveyors of dead sheep probably gave this concept little

thought, outside of their dreams and fevered imaginings.

At some point in history it was probably realized that you can sometimes, if you are a particu

larly fast talker, sell a sheep that you don’t actually own, thus, simultaneously inventing the

important concepts of debt and negative numbers. Having sold this putative sheep, you would in

fact own “negative one” sheep. This would lead to the discovery of integers, which consist of the

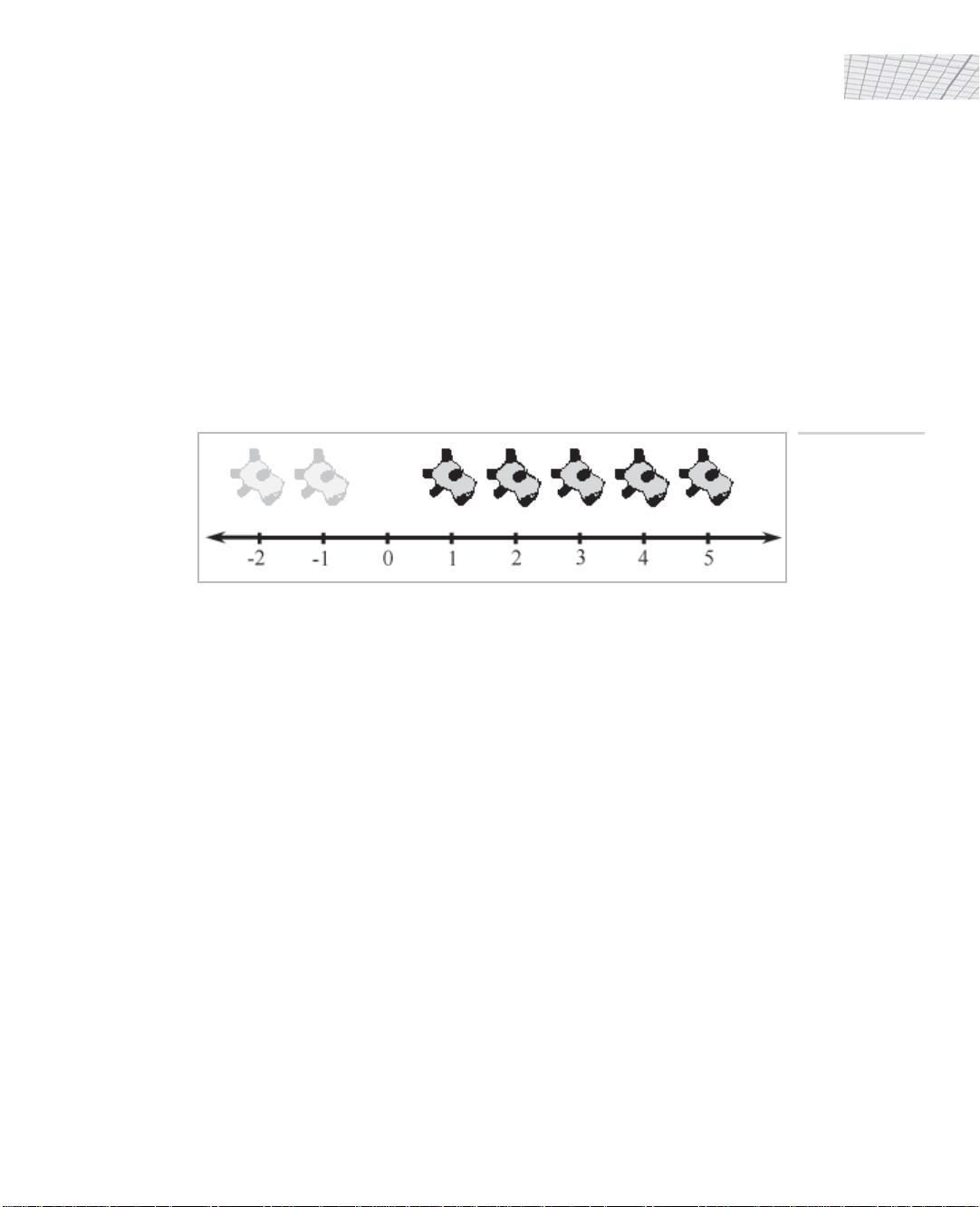
natural numbers and their negative counterparts. The corresponding number line for integers is

shown in Figure 2.3.

The concept of poverty probably predated that of debt, leading to a growing number of people who

could afford to purchase only half a dead sheep, or perhaps only a quarter. This lead to a burgeon-

ing use of fractional numbers, consisting of one integer divided by another, such as 2/3 or 111/27.

Mathematicians called these rational numbers, and they fit in the number line in the obvious

places between the integers. At some point, people became lazy and invented decimal notation,

like writing “3.1415” instead of the longer and more tedious 31415/10000.

After a while, it was noticed that some numbers that appear to turn up in everyday life are not

expressible as rational numbers. The classic example is the ratio of the circumference of a circle to

its diameter, usually denoted as p (pronounced “pi”). These are the so-called real numbers, which

include rational numbers and numbers such as p that would, if expressed in decimal form, require

an infinite number of decimal places. The mathematics of real numbers is regarded by many to be

the most important area of mathematics, and since it is the basis for most forms of engineering, it

can be credited with creating much of modern civilization. The cool thing about real numbers is

that while rational numbers are countable (that is, placed into one-to-one correspondence with the

natural numbers), real numbers are uncountable. The study of natural numbers and integers is

called discrete mathematics, and the study of real numbers is called continuous mathematics.

The truth is, however, that real numbers are nothing more than a polite fiction. They are a rela

tively harmless delusion, as any reputable physicist will tell you. The universe seems to be not

only discrete, but also finite. If there are a finite amount of discrete things in the universe, as cur

rently appears to be the case, then it follows that we can only count to a certain fixed number.

Thereafter, we run out of things to count — not only do we run out of dead sheep, but toasters,

mechanics, and telephone sanitizers also. It follows that we can describe the universe using only

Chapter 2: The Cartesian Coordinate System

Figure 2.3: A

number line for

integers (note the

ghost sheep for

negative

numbers)

剩余448页未读，继续阅读

CodeArhat

粉丝: 13
资源: 55

图形与游戏开发3D数学基础教程

3D数学基础：图形与游戏开发入门

3D数学基础：图形与游戏开发的数学原理

图形与游戏开发3D数学基础指南

3D Math Primer for graphics and game development

3D Math Primer for Graphics and Game Development 2nd

3D Math Primer for Graphics and Game Development.djvu

3D Math Primer for Graphics and Game Development Souce Code

3D Math Primer for Graphics and Game Development 2nd Edition

3D Math Primer for Graphics and Game Development英文版

3D Math Primer for Graphics and Game Development3.rar

最新资源