逻辑回归模型探究与参数估计

"这篇实验报告主要探讨了逻辑回归模型，由哈尔滨工业大学计算机科学与技术学院的学生沈子鸣完成。实验内容包括理解逻辑回归的基本原理，实现两种不同的参数估计方法，即无惩罚项和加入惩罚项，并可以使用梯度下降或共轭梯度法。报告还涉及了实验环境和设计思想，特别提到了sigmoid函数和正则化的应用以防止过拟合。" 在逻辑回归中，主要目标是构建一个模型来预测二分类问题，即输出可能是0或1的标签。模型基于sigmoid函数，它能够将连续的预测值映射到0到1的概率区间，便于转化成离散的类别标签。sigmoid函数的表达式为： \[ f(x) = \frac{1}{1 + e^{-x}} \] 逻辑回归的参数是权重向量 \( w \)，通常通过最大化似然函数来估计。在二项逻辑回归中，似然函数为正例和反例的概率乘积。然而，直接最大化似然函数计算困难，因此通常采用极大条件似然估计（MCLE），计算负对数似然函数，即损失函数。 损失函数通常采用对数损失，无惩罚项时为： \[ L(w) = -\sum_{i=1}^{n} [y_i log(p_i) + (1 - y_i) log(1 - p_i)] \] 其中，\( n \) 是样本数量，\( y_i \) 是第 \( i \) 个样本的真实标签，\( p_i \) 是模型预测的该样本为正类别的概率。 为了避免过拟合，可以引入L1或L2正则化项。L1正则化倾向于产生稀疏解，L2正则化则会使所有权重向量元素趋向于较小但非零的值。在梯度下降或共轭梯度法中，正则化项会添加到损失函数中，导致权重更新的方向和大小发生变化。 对于梯度下降法，损失函数变为： \[ L(w) = -\sum_{i=1}^{n} [y_i log(p_i) + (1 - y_i) log(1 - p_i)] + \lambda \sum_{j=1}^{d} |w_j| \] （L1正则化） 或 \[ L(w) = -\sum_{i=1}^{n} [y_i log(p_i) + (1 - y_i) log(1 - p_i)] + \frac{\lambda}{2} \sum_{j=1}^{d} w_j^2 \] （L2正则化） 其中，\( \lambda \) 是正则化参数，\( d \) 是特征维度。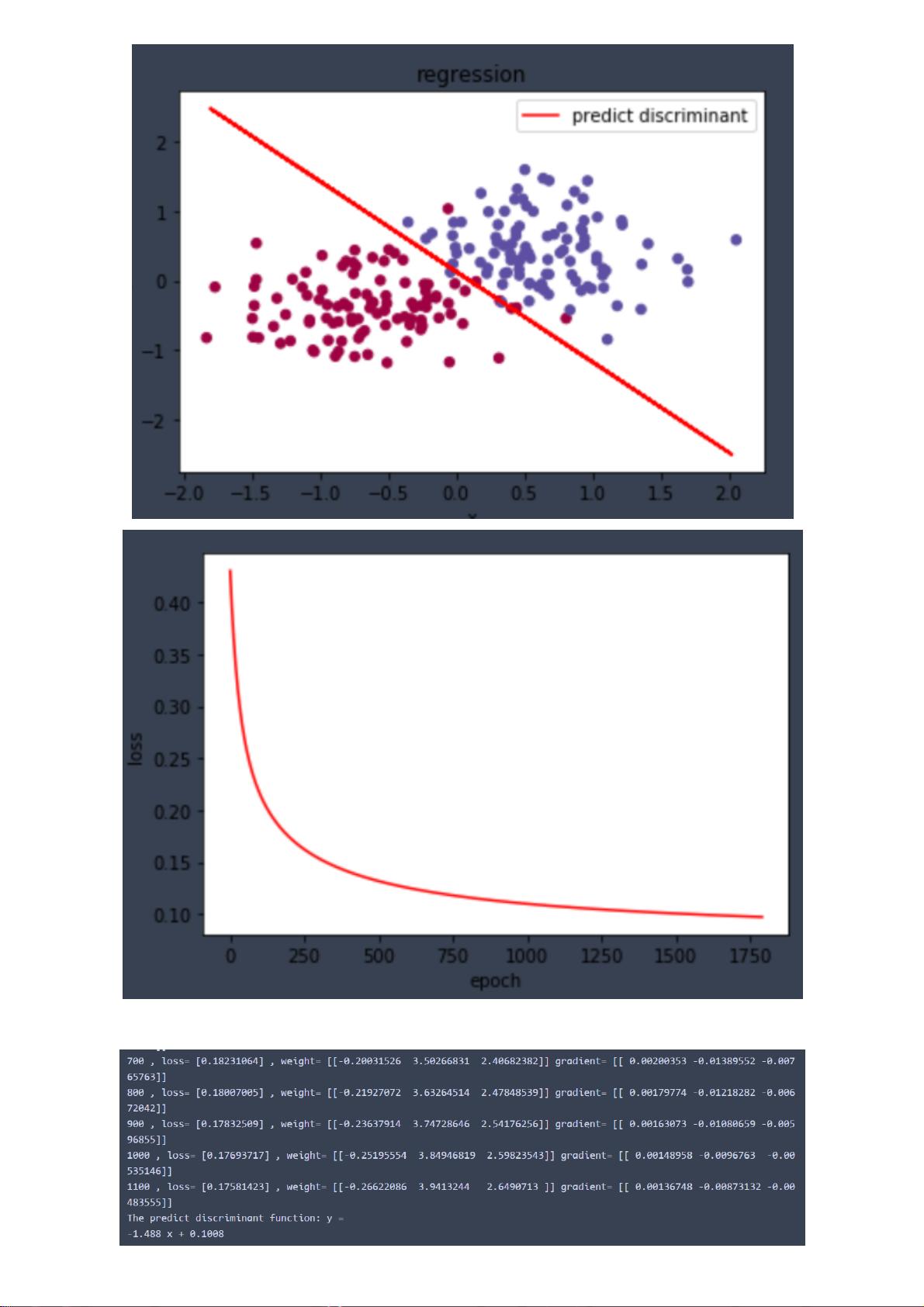 实验报告还讨论了线性决策面的概念，指出决策面的选择往往是最能增大两类样本之间“最短距离”的那一个。这个距离对应于分类边界与最近的样本点之间的间隔，有助于模型泛化能力的提升。 该实验报告深入浅出地介绍了逻辑回归的原理、实现方式以及正则化的应用，对于理解机器学习中的基础分类模型具有重要的参考价值。