C++实现Bellman-Ford算法：处理任意权值的单源最短路径

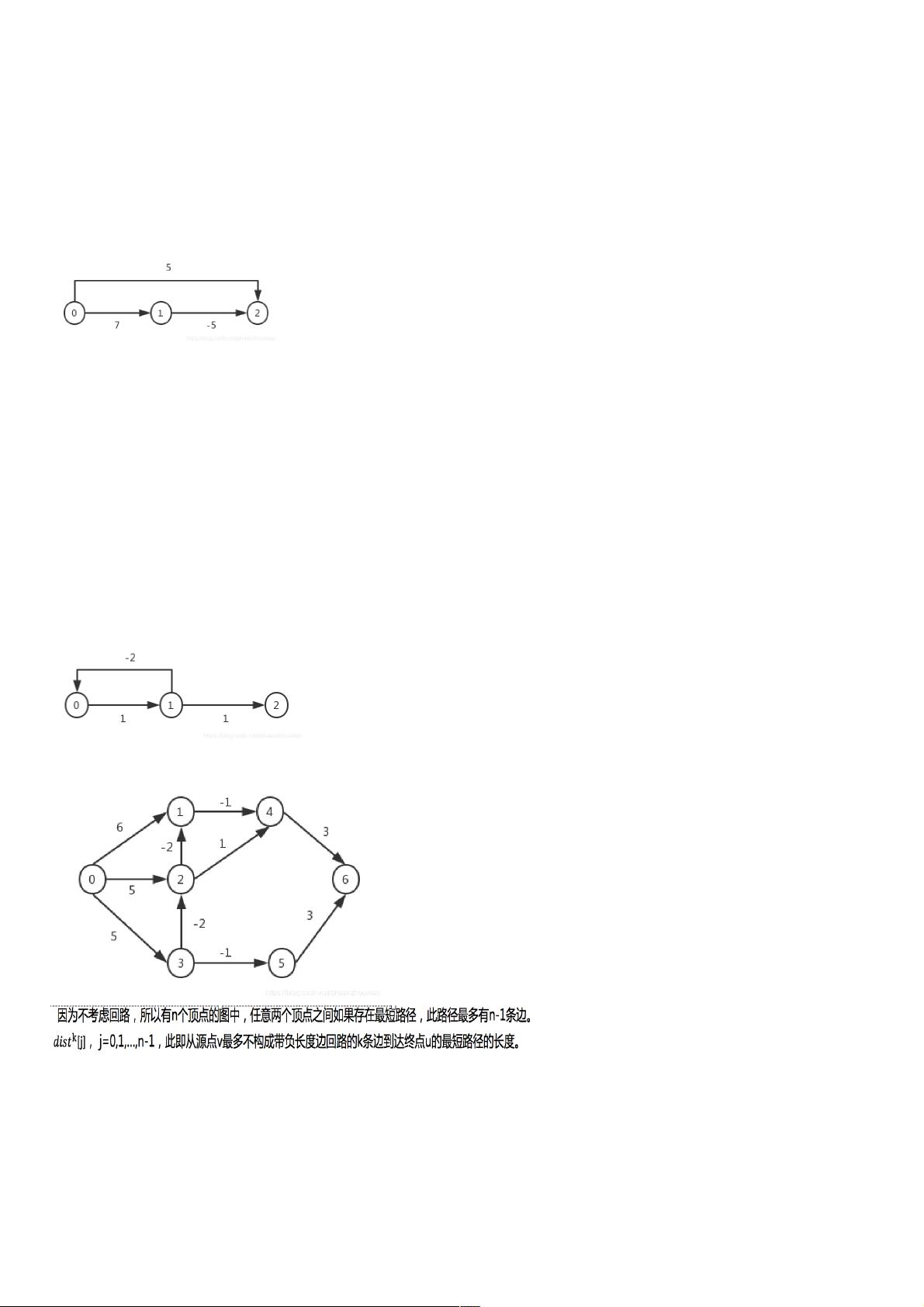
在IT领域，C++编程语言中处理图论问题时，单源最短路径是一个常见的需求。这里讨论的是如何使用Bellman-Ford算法来计算任意权值的单源最短路径，特别是在Dijkstra算法无法处理负权边的情况。Dijkstra算法基于贪心策略，只适用于非负权值图，一旦遇到负权边，可能会得到错误的结果。 Bellman-Ford算法是一种更为通用的求解单源最短路径的方法，特别适用于包含负权边的图。该算法的基本思想是进行多次迭代，每次迭代检查所有边，如果发现通过某个中间节点可以形成更短的路径，就更新目标节点的距离。这个过程会持续n-1次，其中n是图中的顶点数量，因为最多可能需要经过n-1步才能达到最远的顶点。在每次迭代后，都会确保已经找到了所有顶点到源点的最短路径，如果没有发现更短路径，那么算法可以确定结果是正确的，因为不可能再通过更多的边得到更短路径（存在负权回路的情况除外）。 例如，对于一个有向图，初始时顶点0到顶点1的距离可能是6，但通过一条负权边（如0->2->3，总距离为5-2=3），在第二轮迭代中，我们可能会发现更短的路径。这个过程不断重复，直到没有新的路径可以优化为止。 在C++实现上，代码通常会包括一个循环，内含一个for循环遍历所有顶点，每次更新距离数组（dist[]）和路径数组（path[]）。算法结束后，dist[]数组将存储每个顶点到源点的最短路径长度，而path[]则记录了这些最短路径的具体路径序列。 需要注意的是，Bellman-Ford算法的时间复杂度为O((V+E)×n)，其中V是顶点数，E是边数，这意味着它对于大规模图可能效率较低，但在需要处理负权边的情况下，它是必要的选择。对于Dijkstra算法，时间复杂度为O((V+E)logV)，这在无负权边的情况下更为高效。 C++中的Bellman-Ford算法是一个重要的工具，它能够处理复杂的单源最短路径问题，并且在实际编程中提供了可靠的解决方案。掌握这一算法，程序员可以在处理实际问题时灵活应对不同类型的图结构。