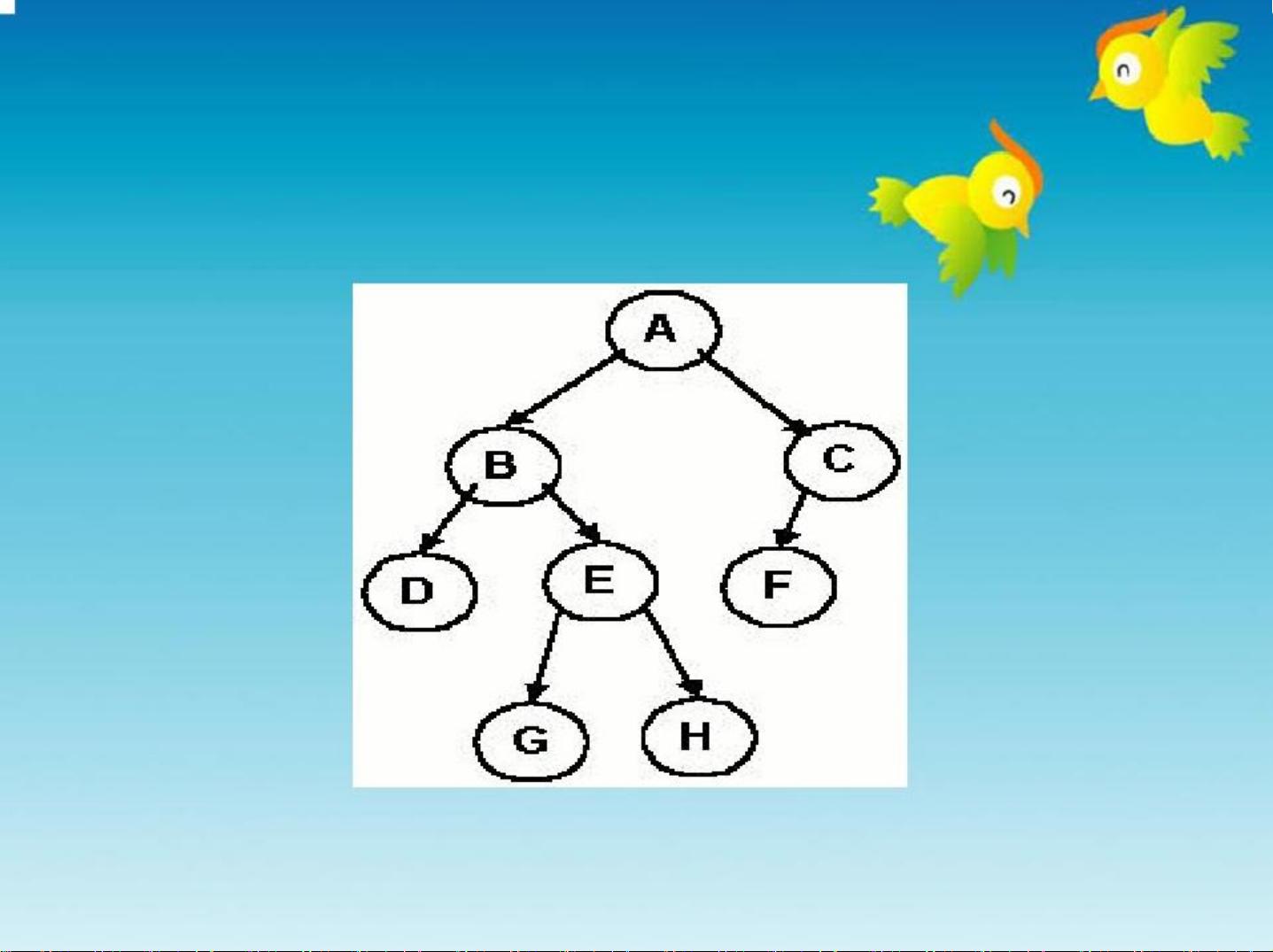
二叉树遍历：先序、中序、后序与层次解析

"二叉树的遍历是计算机科学中处理二叉树数据结构的一种基本操作，包括先序遍历、中序遍历、后序遍历和层次遍历。这些遍历方法通常采用递归和非递归两种算法实现。在二叉树的遍历过程中，节点的访问顺序对于理解和操作二叉树至关重要。" 二叉树遍历是数据结构领域中的核心概念，它涉及到对二叉树中的每个节点按照特定顺序进行访问。下面将详细解释四种主要的遍历方式： 1. **先序遍历（Preorder Traversal）**： - 访问顺序：根 -> 左子树 -> 右子树 - 在递归实现中，先访问当前节点，然后递归地遍历左子树，最后遍历右子树。非递归实现通常使用栈来模拟递归过程。 - 示例代码中的`void preorder(BTreeNode<T> *p, void visit(BTreeNode<T> *p))`函数实现了先序遍历。 2. **中序遍历（Inorder Traversal）**： - 访问顺序：左子树 -> 根 -> 右子树 - 对于二叉搜索树，中序遍历可以得到节点值的升序序列。 - 递归实现时，先遍历左子树，然后访问当前节点，最后遍历右子树。非递归实现同样可以使用栈来完成。 3. **后序遍历（Postorder Traversal）**： - 访问顺序：左子树 -> 右子树 -> 根 - 后序遍历在处理二叉树的复制和删除操作时非常有用。 - 递归实现中，首先遍历左子树和右子树，最后访问当前节点。非递归实现可能需要两个栈，一个用于存储待访问的节点，另一个用于保存已访问节点。 4. **层次遍历（Level Order Traversal）**： - 访问顺序：从根开始，逐层遍历，同一层的节点从左到右访问 - 层次遍历常用于二叉树的宽度优先搜索（BFS），常用队列实现。 - 示例代码中的`void layerorder(void visit(BTreeNode<T> *p))`函数用于层次遍历。 在实际应用中，二叉树遍历常被用于查找、排序、复制、删除等操作。递归和非递归算法各有优缺点：递归实现简洁直观，但可能导致栈溢出；非递归算法通常需要额外的数据结构，但避免了递归带来的问题。 二叉树遍历的理解和熟练掌握对于学习和解决计算机科学中的许多问题至关重要，特别是在数据结构、算法设计以及编译原理等领域。通过这些遍历方法，我们可以有效地遍历和操作二叉树，进而解决更复杂的问题。