最小二乘法详解：多项式拟合关键原理

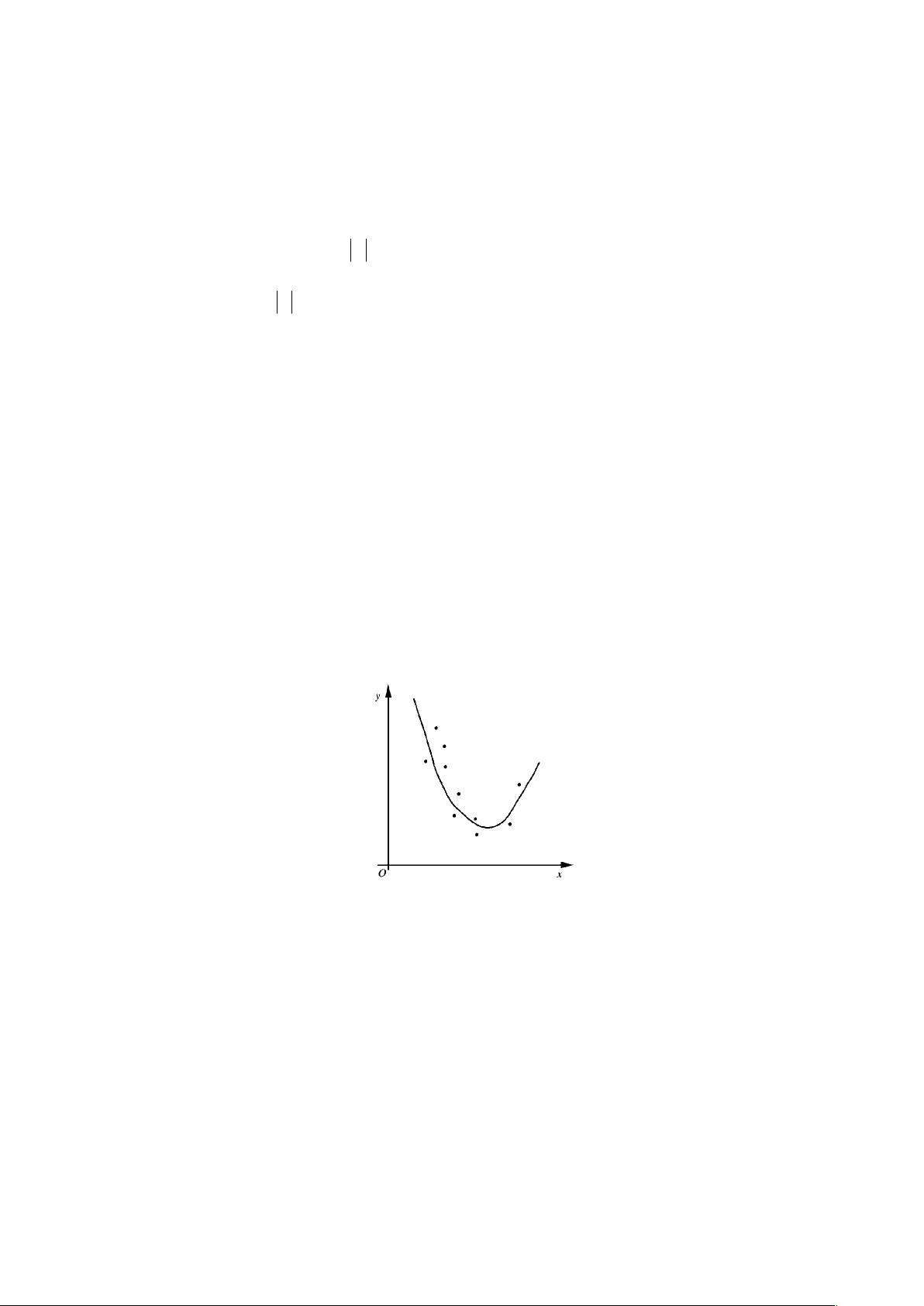
最小二乘法是一种广泛应用在统计学、机器学习和工程领域中的优化技术，它的基本原理是通过寻找一个函数，使得这个函数在一组数据点上的误差平方和最小化。这种方法在数据拟合和模型构建中尤其重要，因为它能提供一个简洁且可微分的解决方案。 首先，最小二乘法的核心思想是衡量误差的常用方法，包括绝对误差的最大值（∞范数）、误差的总和（1范数）以及误差平方和（2范数）。尽管前两者直观，但在实际计算中，2范数由于方便微分，常常被选为首选，因为它对应于误差的平方和，可以直接转化为欧几里得距离，直观地体现了数据点到拟合曲线的平均偏差。 在曲线拟合过程中，具体做法是选择一个给定的数据集，如[pic]中的(i=0,1,...,m)，在给定的函数类别[pic]中找到一个函数[pic]，使得这些数据点与其对应的函数值的误差平方和达到最小。这个最小化问题可以形式化为求解[pic]，使得[pic]，这实质上是一个优化问题，可以通过微分方法解决。 如果选择多项式作为函数类别，就形成了多项式拟合。例如，如果数据点是[pic]，而[pic]表示所有次数不超过n的多项式，那么目标是找到一个多项式[pic]，使得[pic]满足（1）。特别地，n=1时的线性拟合或直线拟合是最基础的情况。 求解多项式拟合的问题，可以将其转化为多元函数的极值问题。根据多元函数极值的必要条件，我们可以得到[pic]的线性方程组（3），进一步用矩阵形式表示为（4）。这个方程组被称为正规方程组或法方程组，它保证了系数矩阵是一个对称正定矩阵，这意味着存在且唯一解。 解出该线性方程组后，我们可以得到多项式的形式[pic]，其中[pic]被称为最小二乘拟合多项式的平方误差。这种拟合方式不仅确保了拟合效果好，而且计算过程相对直接，易于理解和实施。 总结来说，最小二乘法通过最小化误差平方和，提供了有效的方法来估计和拟合数据，尤其是在多项式拟合中，通过正规方程组的求解，我们可以得到精确的多项式表达式，这对于数据分析、模型预测等任务具有重要意义。