图论基石：最短路径、拓扑排序与关键路径详解

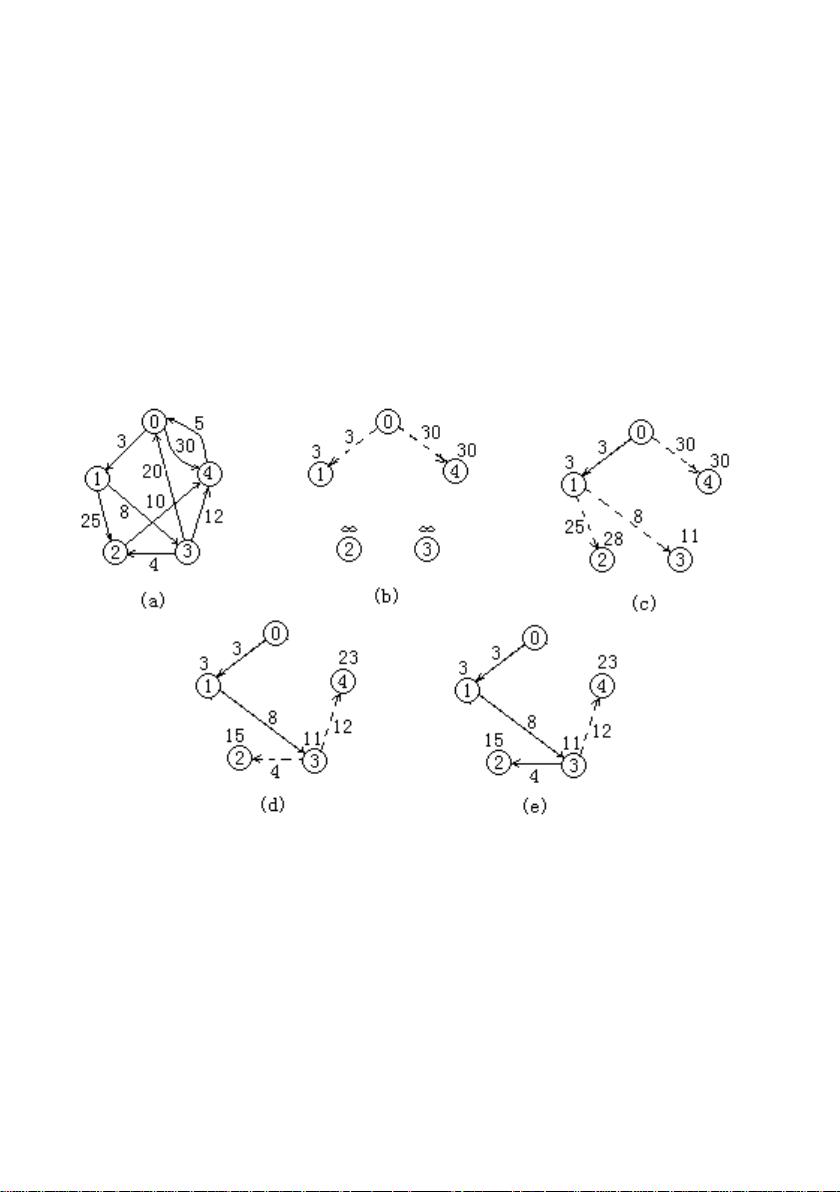
在数据结构课程中，图的最短路径、拓扑排序和关键路径是重要的概念。最短路径问题主要研究在有向或无向图中，从一个顶点到另一个顶点的路径中，如何找到路径长度最短的那条，无论是无权图中的简单边数量，还是带权图中边的权值之和。带权图中的最短路径问题更为广泛，因为可以将无权图视为所有边权重均为1的有向图。这种问题在实际应用中常见，如城市交通网络中，寻找两点之间的最短运输路线或最小运费。 最短路径问题分为两类：一是单源最短路径，即从指定的源点（如起点城市）到图中其他所有顶点的最短路径；二是所有对顶点之间的最短路径。对于单源最短路径问题，可能的路径包括直接相连的边，或者经过多个中间顶点的组合路径。例如，在图3-1中，从v0到v4的最短路径就是通过<0,1,3,4>这条路径，而不是仅考虑直接相连的边。 拓扑排序是一种对有向无环图（DAG）进行排序的方法，按照一定的顺序排列图中的顶点，使得对于任意一条有向边(i, j)，顶点i总是排在顶点j之前。这种排序没有固定顺序，不同的图可能会有不同的拓扑排序结果。拓扑排序在依赖关系分析、任务调度等领域有广泛应用，例如确定项目执行的先后顺序，避免循环依赖。 关键路径是图中决定整个任务完成时间最长的路径，它包含从起点到终点的最短路径，并且这些路径上的所有边都不允许延误，否则将影响整个任务的完成时间。关键路径的识别对于项目管理和优化至关重要。 在C++编程中，这些问题可以通过各种算法来解决，如迪杰斯特拉算法（Dijkstra's algorithm）用于单源最短路径，贝尔曼-福特算法（Bellman-Ford algorithm）适用于带有负权边的图，而拓扑排序则可以通过深度优先搜索（DFS）或拓扑排序算法实现。掌握这些算法不仅可以帮助理解理论概念，也能在实际开发中提高效率。