ATLAS探测器在13 TeV pp碰撞中寻找与W/Z玻色子关联的暗物质

164 浏览量更新于2024-07-16 收藏 1.47MB PDF 举报

"使用ATLAS探测器搜索碰撞中与强子衰变矢量玻色子相关的暗物质" 这篇研究文章是关于在大型强子对撞机（LHC）上使用ATLAS探测器进行的一项实验，该实验旨在寻找与强子衰变的W或Z玻色子相关联的暗物质。在s = 13 TeV能量下的pp碰撞数据中，研究人员分析了3.2 fb$^{-1}$的数据集，即3.2 femtobarns的逆面积。在这个过程中，他们关注的是那些表现出与W或Z玻色子衰变相符的强子束射流以及具有显著横向动量缺失的事件。这种横向动量缺失是暗物质存在的间接证据，因为它无法被探测到，但可以通过它对可检测粒子的动量不平衡来推断。 ATLAS探测器是LHC的一个复杂仪器，它能够探测并测量高能粒子碰撞的各种结果，包括可能与暗物质相互作用的事件。在这项研究中，科学家们比较了观测到的数据与标准模型的预测，标准模型是描述已知基本粒子和力的理论框架。数据的分析显示，观测结果与标准模型的预期一致，没有发现超出预期的现象。为了更深入地解释这些结果，研究团队采用了两种理论框架：有效场论（Effective Field Theory, EFT）和简化模型（Simplified Models）。EFT允许研究人员在不完全了解新物理现象的具体细节的情况下，对其可能的影响进行建模。而简化模型则引入了暗物质粒子及其与普通物质相互作用的特定假设，帮助科学家理解可能的信号。在EFT的框架下，研究人员探索了暗物质与W或Z玻色子的耦合可能如何影响碰撞事件的特征。同时，通过简化模型，他们考察了暗物质粒子可能的质量范围和与常规粒子的相互作用强度。尽管没有直接观察到暗物质粒子，但这些研究有助于限制这些模型的参数空间，从而进一步指导未来的搜索策略。最后，值得注意的是，这篇文章是开放获取的，这意味着公众和同行研究者可以自由访问和使用这些研究成果。这是科学研究的透明性和合作精神的重要体现，也是通过SCOAP3（促进开放科学的合作出版计划）资助的。此外，该研究遵循了Creative Commons Attribution 4.0许可证，允许他人在遵守一定条件的情况下自由使用、分发和修改文章内容。这项研究是寻找暗物质的前沿工作，通过高能粒子碰撞的观测数据，利用ATLAS探测器的精确测量能力，为理解宇宙中这一神秘成分提供了重要的线索。

254 The ATLAS Collaboration / Physics Letters B 763 (2016) 251–268

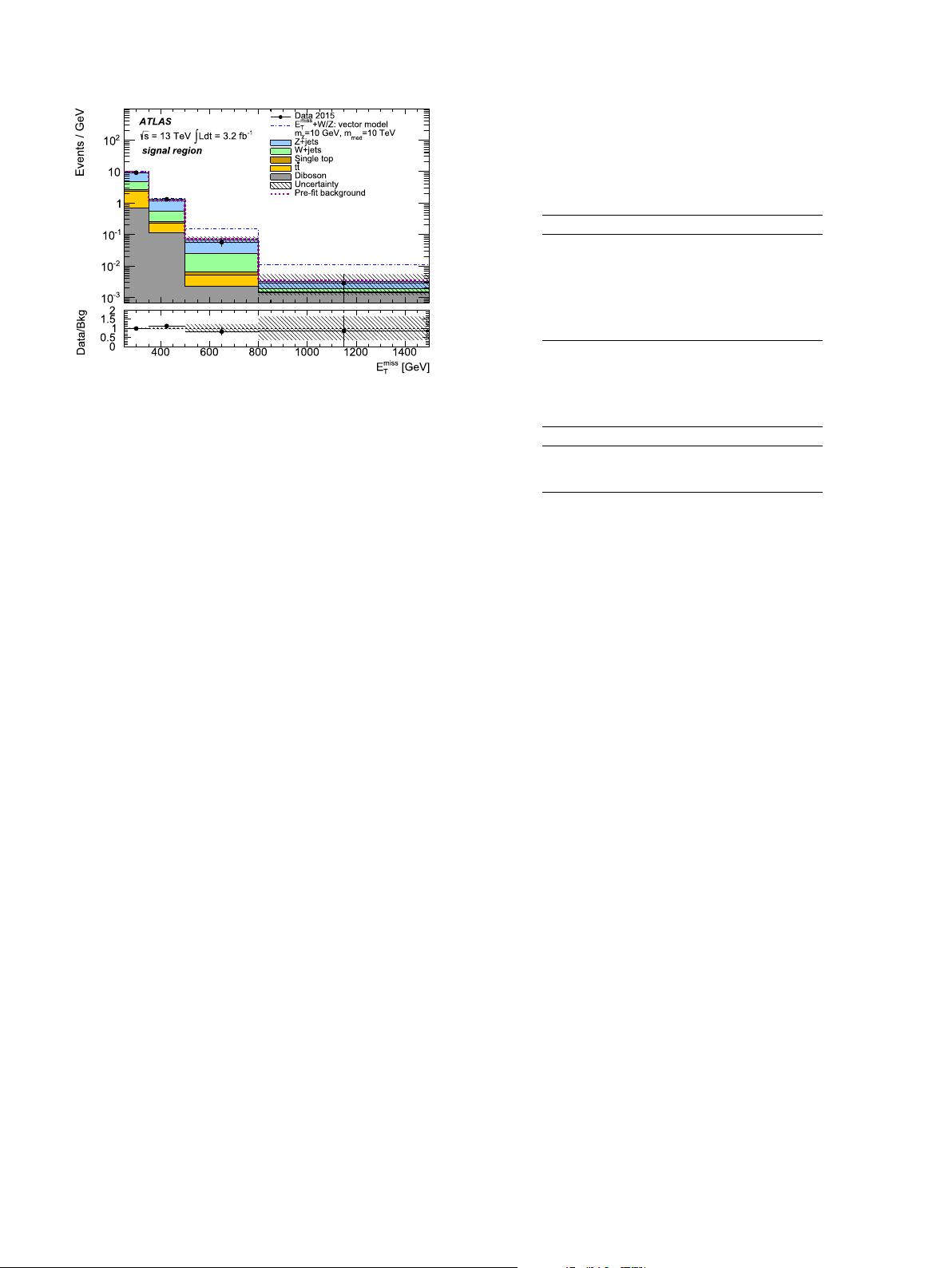
Fig. 4. The E

miss

distribution of the events in the signal region after the proﬁle-

likelihood

ﬁt to the data under the background-only hypothesis. The inset shows

the ratio of the data to the total background. Also shown is the E

miss

distribution

for the simpliﬁed model with a vector-boson mediator, scaled by a factor of 10

for

=10 GeV and m

med

=10 TeV. The total background before the ﬁt is shown as a

dashed line. The hatched bands represent the total uncertainty in the background.

(For interpretation of the references to color in this ﬁgure legend, the reader is re-

ferred

to the web version of this article.)

Samples of simulated W χ

χ and Z χ

χ events are generated us-

ing MadGraph5_aMC@NLO [55],

and the underlying event and par-

ton

showering are simulated with Pythia8.186 [53]. Two theoret-

ical

models are used as benchmarks: a seven-dimensional VVχχ

EFT [19] model (V meaning W or Z ) and a vector-mediated sim-

pliﬁed

model [56]. The strength of the EFT interaction is controlled

by a mass scale, M



, and the strength of the simpliﬁed model

interaction is controlled by the product of the couplings of the

mediator to the SM and the dark matter (DM) particles, g

The EFT model samples were generated with M



= 3000 GeV,

and the simpliﬁed model samples were generated with couplings

= 0.25 and g

= 1. The samples were generated as a func-

tion

of dark-matter particle mass m

for the EFT model and in a

grid of mediator mass m

med

and m

for the simpliﬁed model.

Major

sources of systematic uncertainty are uncertainties in the

modelling of large-R jet observables, which have a 5–13% impact

on the expected background and signal yields, and the energy

scale of the narrow jets, which contribute a 1–5% uncertainty to

the expected yields. Other sources of uncertainty include theoret-

ical

uncertainties in the simulated event samples used to model

the background processes (1–10%), parton distribution functions

(10–15%), and lepton reconstruction and identiﬁcation eﬃciencies

(up to 2%).

proﬁle-likelihood ﬁt [57] to the E

miss

,noμ

) distribution in

the signal region (control regions) is used to constrain the W bo-

son,

Z boson, and t

t backgrounds and extract the signal strength,

μ, for each model as an overall normalization factor for the signal

prediction. Besides the signal strength, three overall normalization

factors for the W boson, Z boson, and t

t backgrounds are pa-

rameters

in the ﬁt. The diboson and single-top backgrounds are

estimated from simulation, and the multijet background is negli-

gible.

The likelihood function is deﬁned as the product of Poisson

distributions over all bins in E

miss

and E

miss

,noμ

, and the likelihood

is simultaneously maximized over the signal and control regions.

Variations

of the expected signal and background to allow for

their systematic uncertainties are described with nuisance parame-

ters

constrained by Gaussian probability distribution functions, and

correlations across signal and background processes and regions

are taken into account.

Table 1

Predicted

and observed number of events in the signal re-

gion.

The yields and uncertainties of the backgrounds are

shown after the proﬁle-likelihood ﬁt to the data under the

background-only hypothesis. For comparison, the expected

yield in the VVχχ EFT model with M



= 600 GeV and

=500 GeV is 10.1 ±0.4events.

Process Events

Z + jets 544 ±33

+ jets 275 ±24

t and single-top 211 ±19

Diboson 89

±12

Total background 1120

±47

Data 1121

Table 2

Background

normalization factors relative to the initial

theoretical prediction, extracted from the proﬁle-likelihood

ﬁt under the background-only hypothesis.

Process Normalization factor

Z + jets 1.01 ±0.16

+ jets 0.90 ±0.16

t 0.91 ±0.18

A background-only (μ = 0) ﬁt, shows no deviation from SM

predictions, and Figs. 3 and 4 show kinematic distributions af-

ter

the proﬁle-likelihood ﬁt. The ﬂoating background-normalization

parameters are consistent with unity within one standard devia-

tion.

Tables 1 and 2 show the expected event yields after applying

the signal selection and the background normalization scale fac-

tors,

respectively. The values in these tables are estimated for the

background-only hypothesis.

Upper

limits at 95% conﬁdence level (C.L.) on μ are calculated

using the CL

method [58]. For the VVχχ EFT model, these lim-

its

are translated into constraints on the mass scale, M



. Fig. 5(a)

shows the limit on the mass scale, M



, in the EFT model, as a func-

tion

of m

. Fig. 5(b) shows the limits on the signal strength, μ,

for a vector-mediated simpliﬁed model generated with couplings

=0.25 and g

=1in the plane of m

and m

med

conclusion, this Letter reports ATLAS limits on dark-matter

production in events with a hadronically decaying W or Z bo-

son

and large missing transverse momentum. These limits from

3.2 fb

−1

of 13 TeV pp collisions at the LHC improve on earlier AT-

LAS

results. No statistically signiﬁcant excess is observed over the

Standard Model prediction.

Acknowledgements

We thank CERN for the very successful operation of the LHC,

as well as the support staff from our institutions without whom

ATLAS could not be operated eﬃciently.

acknowledge the support of ANPCyT, Argentina; YerPhI, Ar-

menia;

ARC, Australia; BMWFW and FWF, Austria; ANAS, Azerbai-

jan;

SSTC, Belarus; CNPq and FAPESP, Brazil; NSERC, NRC and CFI,

Canada; CERN; CONICYT, Chile; CAS, MOST and NSFC, China; COL-

CIENCIAS,

Colombia; MSMT CR, MPO CR and VSC CR, Czech Re-

public;

DNRF and DNSRC, Denmark; IN2P3-CNRS, CEA-DSM/IRFU,

France; GNSF, Georgia; BMBF, HGF, and MPG, Germany; GSRT,

Greece; RGC, Hong Kong SAR, China; ISF, I-CORE and Benoziyo

Center, Israel; INFN, Italy; MEXT and JSPS, Japan; CNRST, Mo-

rocco;

FOM and NWO, Netherlands; RCN, Norway; MNiSW and

NCN, Poland; FCT, Portugal; MNE/IFA, Romania; MES of Russia and

NRC KI, Russian Federation; JINR; MESTD, Serbia; MSSR, Slovakia;

ARRS and MIZŠ, Slovenia; DST/NRF, South Africa; MINECO, Spain;

SRC and Wallenberg Foundation, Sweden; SERI, SNSF and Cantons

剩余17页未读，继续阅读

weixin_38546459

粉丝: 7
资源: 915

ATLAS探测器在13 TeV pp碰撞中寻找与W/Z玻色子关联的暗物质

用ATLAS探测器在s = 13 TeV的pp碰撞中搜索与Z玻色子相关的无形衰变的希格斯玻色子或暗物质候选物

使用ATLAS探测器在矢量玻色子融合中搜索不可见的希格斯玻色子衰变

使用ATLAS探测器通过碰撞搜索→在强子最终状态中的衰变

用ATLAS探测器搜索希格斯玻色子衰变→和→碰撞

搜索与ATLAS探测器碰撞时希格斯玻色子的违反轻子味的衰变

使用ATLAS探测器在s = 8 $$ \ sqrt {s} = 8 $$ TeV的pp碰撞中使用矢量-玻色子融合搜索希格斯玻色子的无形衰减

使用ATLAS探测器的快速和位移特征搜索在13 TeV pp碰撞中产生的W玻色子衰变中的重中性轻子

用ATLAS探测器在碰撞的→→衰减通道中测量胶子-胶子融合和矢量-玻色子融合希格斯玻色子产生截面

ATLAS探测器在13 TeV pp碰撞中搜索希格斯玻色子与暗物质关联

ATLAS探测器揭示13 TeV下矢量玻色子融合中不可见希格斯衰变的最新限界

最新资源