动态规划与正态分布：疫苗生产优化问题的五一竞赛解法

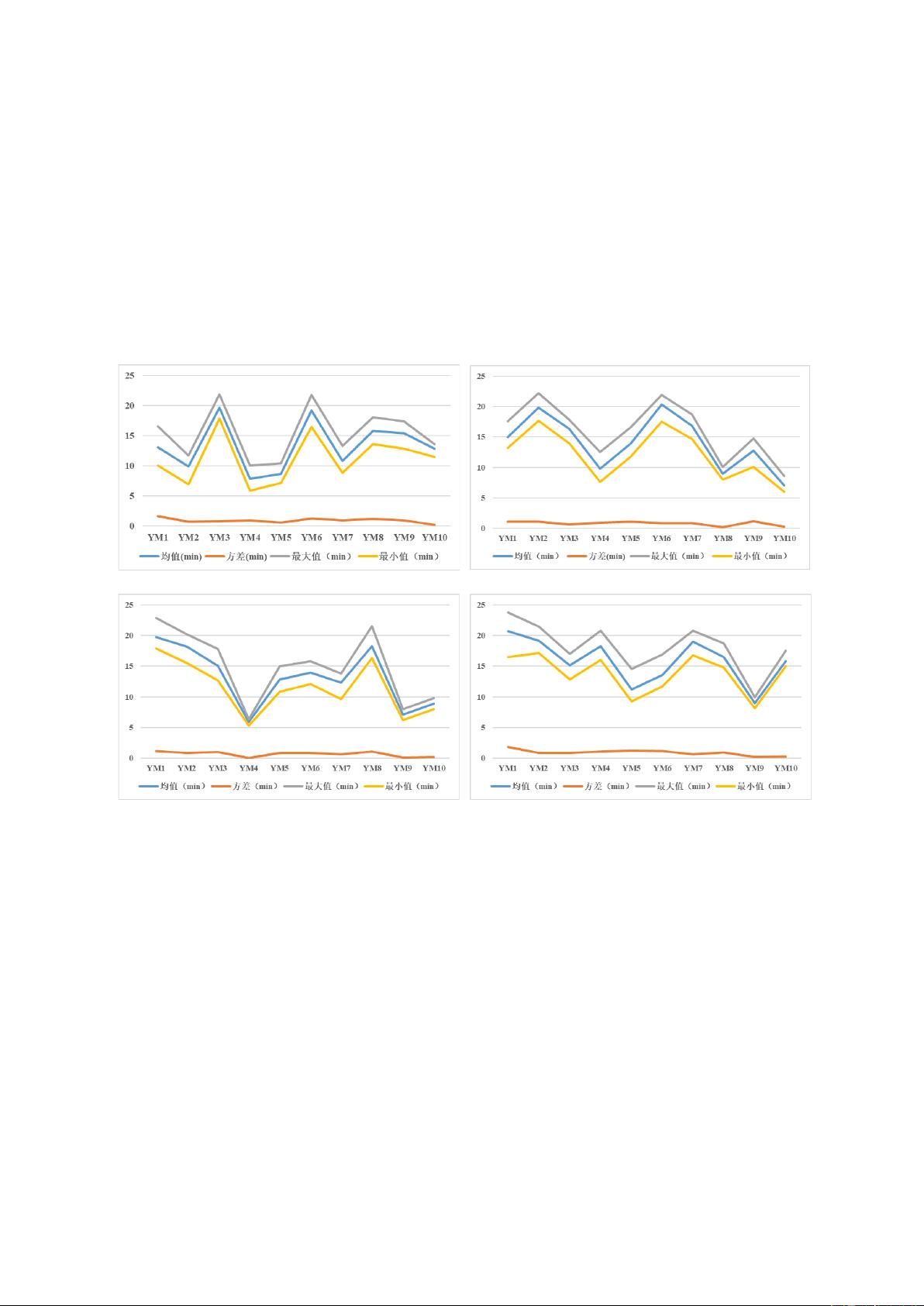
2021年五一数学建模竞赛的A题聚焦于疫苗生产过程的优化问题，主要围绕动态规划、车间排序和调度、以及概率模型等核心概念展开。参赛者针对实际疫苗生产中的挑战，设计了多个解决方案。 首先，针对疫苗生产时间的控制，研究者通过对附件1提供的数据进行深入分析，计算并记录了每个工位生产每箱疫苗的时间分布特征，包括平均值、方差和最值，以便直观展示生产效率。他们发现生产时间符合正态分布，以(13.2840, 1.60)作为均值和方差的例子。 问题二涉及动态规划模型的应用，通过引入0-1变量，对排序后的10种疫苗进行重新编号，目标是优化疫苗加工顺序以减少总加工时间。通过Lingo软件求解，优化后的疫苗加工总时间最短达到188分钟。 进一步，问题三采用概率模型来决定加工顺序，考虑疫苗加工时间的随机性。利用正态分布的特性进行随机采样，计算加工序列在给定概率下的最优组合，如YM4、YM9等依次加工，最大概率为95%。 针对可靠性要求，问题四建立了一个动态规划模型，结合问题三的结果，为不同工位和疫苗类型计算出在90%可靠性的条件下所需加工时间。通过假设法和Lingo软件求解，最低完成任务所需的天数为198天。 最后，问题五将疫苗生产问题转化为经典的多重背包问题，通过朴素算法和二进制编码策略将其转换为0-1背包问题，目标是最大化疫苗的销售额。通过优化后的算法，确定了在满足销售收益最大化的条件下，疫苗的生产配置方案。 这份论文展示了如何运用数学建模技术解决疫苗生产中的实际问题，包括生产时间优化、工作流程安排、概率决策以及资源分配策略，以提升整体生产效率和经济效益。通过这些方法，参赛者不仅提升了疫苗生产的灵活性，还展示了严谨的数学思维和实际应用能力。