C语言实现Prim最小生成树算法详解

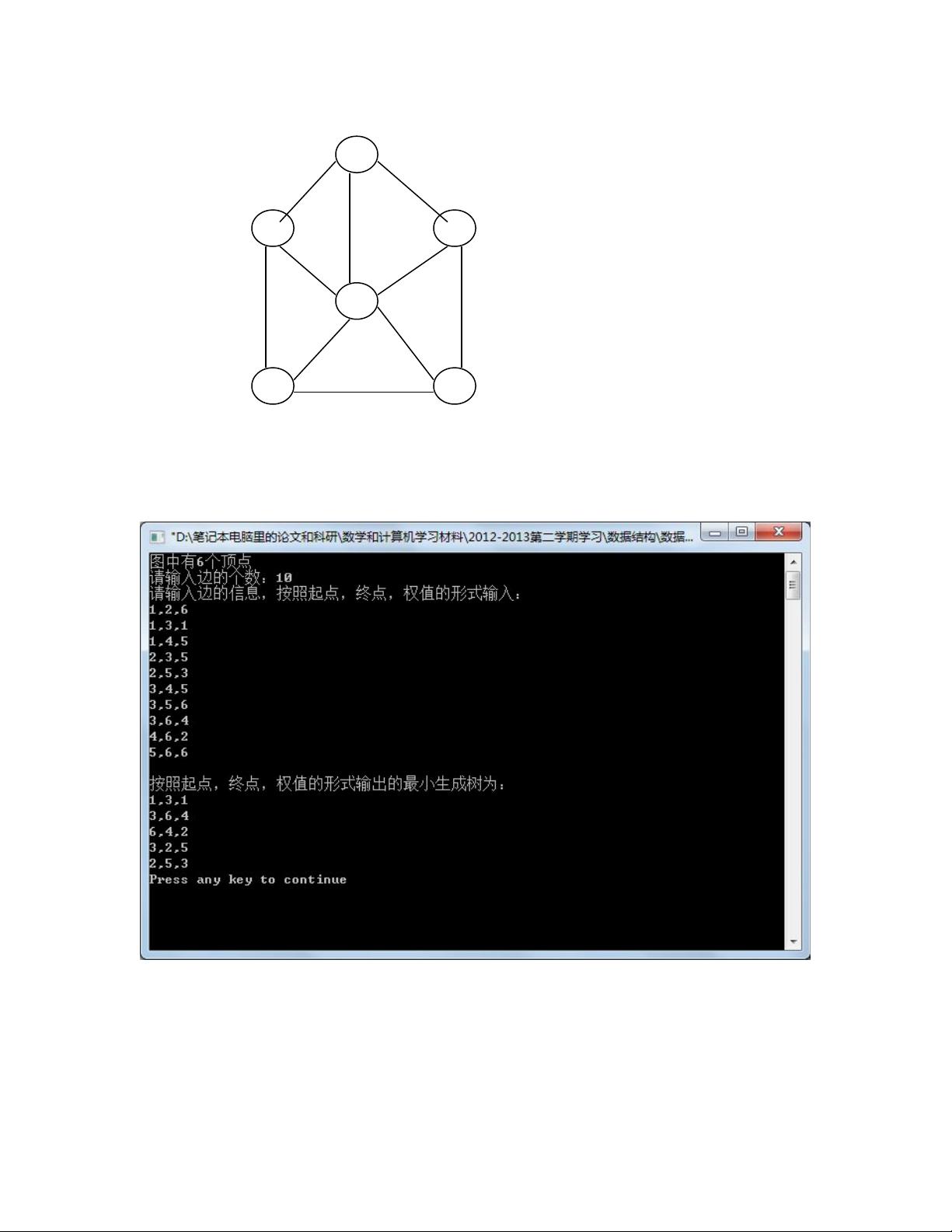
"这篇资源是关于使用C语言实现Prim算法的教程，包含了程序代码和测试例子。Prim算法是一种用于寻找图中最小生成树的经典算法，适用于加权无向图。文章通过创建邻接矩阵来表示图，然后逐步构建最小生成树。" 在计算机科学中，Prim算法是解决网络优化问题的一种方法，它主要用于找到加权无向图中的最小生成树。最小生成树是一棵树形子图，包含了原图的所有顶点，且边的权重之和最小。Prim算法采用贪心策略，每次从当前已选择的顶点集合中找到与未选顶点相连的边中权重最小的一条，将该边的另一端顶点加入集合。 在提供的代码中，首先定义了必要的数据结构和常量。`adjmatrix` 是一个二维数组，用来表示邻接矩阵，其中`n`表示顶点的数量，`MaxNum`用于初始化邻接矩阵，设定一个较大的数值表示无边或边权重无穷大。`Edge` 结构体用于存储边的起始顶点、结束顶点和权重，`EdgeNode` 是指向`Edge`结构体的指针。 接着，`CreatMatrix` 函数用于初始化邻接矩阵，根据用户输入构建图的结构。用户需输入顶点数量和边的信息（起点、终点、权值），程序将这些信息存储到邻接矩阵中。 `InitEdge` 函数初始化边集数组，将所有边的权重设为0，这将在计算最小生成树时使用。 `GetEdgeSet` 函数根据邻接矩阵生成边集数组，只包含非零权重的边，即实际存在的边。这个函数会跳过对角线元素（因为它们表示顶点到自身的边，权重为0）以及矩阵中的最大值（代表不存在的边）。 `SortEdge` 函数对边集数组进行升序排序，这样可以确保每次添加的边是当前未被包含的边中权重最小的一条。 在Prim算法的具体实现中，通常会使用一个优先队列（如二叉堆）来快速获取当前最小的边。然而，这里的代码没有显示这部分，可能是通过循环和临时变量`k`来寻找当前最小权重边的。算法的核心步骤包括： 1. 初始化最小生成树为任意一个顶点。 2. 在剩余的顶点中，找到与最小生成树连接的边中权重最小的一条。 3. 将这条边的另一端顶点加入最小生成树，并更新邻接矩阵或边集数组。 4. 重复步骤2和3，直到所有顶点都包含在内。 Prim算法的时间复杂度为O(ElogE)或O(ElogV)，其中E是边的数量，V是顶点的数量，这取决于优先队列的实现。对于稠密图（E接近V^2）和稀疏图（E远小于V^2）来说，Prim算法都有较好的性能。