C语言实现二叉树遍历及概念解析

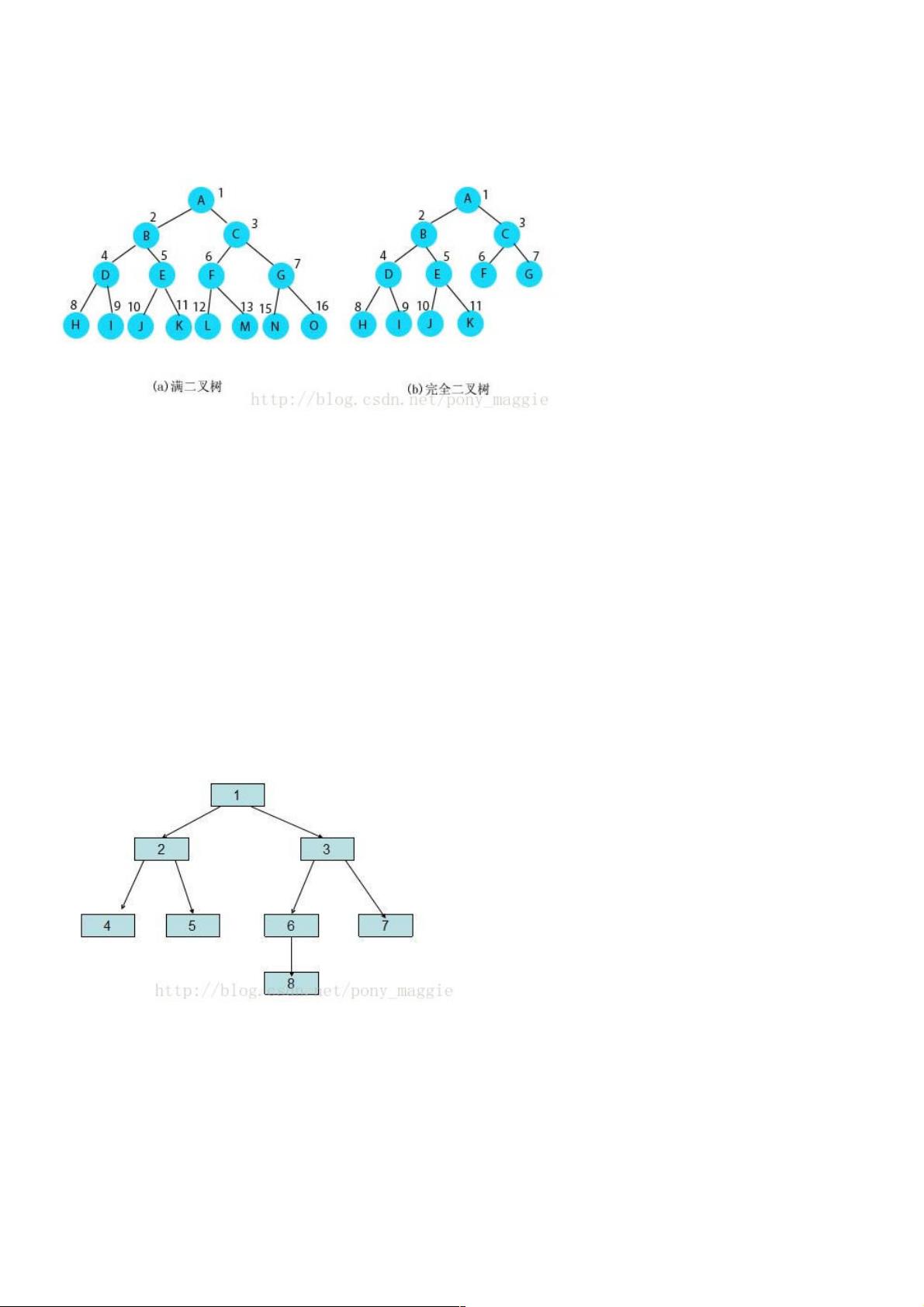
"C语言二叉树几种遍历方法详解及实例" 在计算机科学中，二叉树是一种特殊的树形数据结构，其中每个节点最多有两个子节点，通常称为左子节点和右子节点。二叉树分为不同类型，如满二叉树和完全二叉树。满二叉树是所有非叶节点都有两个子节点的二叉树，而完全二叉树是每一层（除了可能的最后一层）都被完全填满，并且所有节点尽可能地集中在树的左侧的二叉树。因此，满二叉树一定是完全二叉树，但反之不成立。 二叉树的深度是指从根节点到最远叶节点的最长路径上的边数。例如，一个深度为k的二叉树最多可以有2^k - 1个节点。此外，二叉树中的节点间存在特定关系：孩子节点是直接连接到父节点的节点，兄弟节点是具有相同父节点的节点，而父节点则是其子节点的直接上级。 在C语言中实现二叉树时，通常采用链式存储结构，因为顺序存储会导致大量空间浪费。链式结构定义了一个包含数据、指向左子节点和右子节点指针的结构体。创建二叉树通常通过递归进行，根据用户输入或预定义的序列来决定节点的左右子树是否存在。 二叉树的遍历是访问其所有节点的过程，常见的遍历方法有三种：先序遍历、中序遍历和后序遍历。 1. 先序遍历（根-左-右）：首先访问根节点，然后递归地遍历左子树，最后遍历右子树。 2. 中序遍历（左-根-右）：首先遍历左子树，然后访问根节点，最后遍历右子树。对于二叉搜索树，中序遍历会得到节点值的升序序列。 3. 后序遍历（左-右-根）：首先递归地遍历左子树和右子树，最后访问根节点。后序遍历在计算节点的子树大小时非常有用。 遍历二叉树的C语言实现通常涉及递归函数，如下所示： ```c void PreOrderTraversal(pBiTree root) { if (root != NULL) { printf("%d ", root->data); // 访问根节点 PreOrderTraversal(root->leftChild); // 遍历左子树 PreOrderTraversal(root->rightChild); // 遍历右子树 } } void InOrderTraversal(pBiTree root) { if (root != NULL) { InOrderTraversal(root->leftChild); // 遍历左子树 printf("%d ", root->data); // 访问根节点 InOrderTraversal(root->rightChild); // 遍历右子树 } } void PostOrderTraversal(pBiTree root) { if (root != NULL) { PostOrderTraversal(root->leftChild); // 遍历左子树 PostOrderTraversal(root->rightChild); // 遍历右子树 printf("%d ", root->data); // 访问根节点 } } ``` 这些函数可以通过给定的二叉树根节点调用，以按照指定的遍历顺序打印出节点的值。理解并能熟练运用这些遍历方法对于理解和操作二叉树至关重要，它们在算法设计和数据结构的学习中扮演着重要角色。