最小二乘法与多项式拟合原理解析

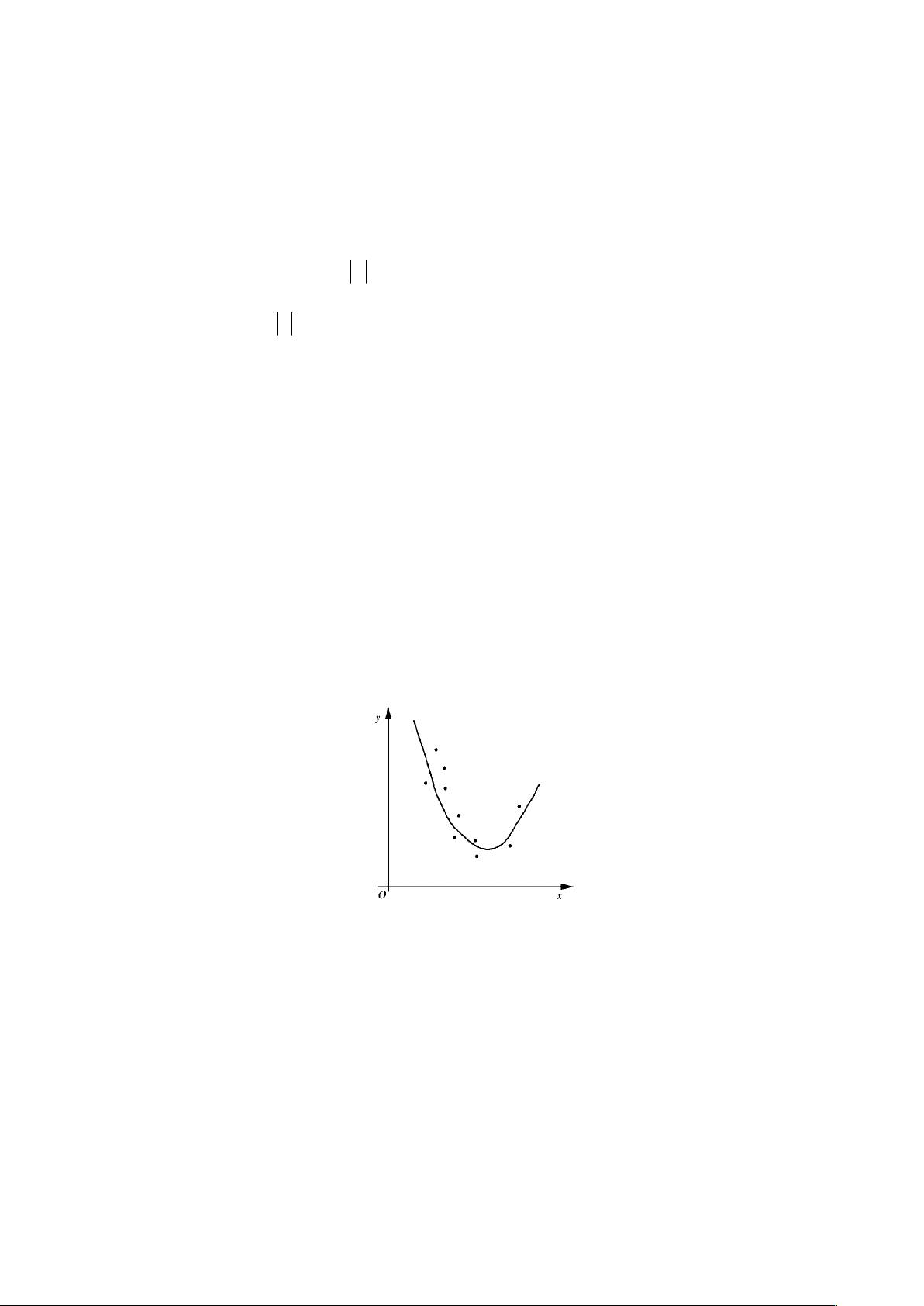
本文主要介绍了最小二乘法的基本原理及其在多项式拟合中的应用。最小二乘法是一种常见的数据拟合方法，通过最小化误差平方和来寻找最佳拟合曲线。这种方法在处理实际问题时具有较高的计算效率和实用性。 一、最小二乘法的基本原理 最小二乘法的核心思想是找到一个函数，使得该函数与给定数据点之间的误差平方和最小。误差平方和是指每个数据点到拟合曲线距离的平方和。在数学表达式中，如果给定数据点 (x_i, y_i) (i=0,1,...,m)，拟合函数为 f(x)，则误差平方和 E 可以表示为： \[ E = \sum_{i=0}^{m}(f(x_i) - y_i)^2 \] 在曲线拟合中，通常选择误差平方和作为衡量拟合优度的标准，因为它便于进行微分运算，有助于求解极值问题。 二、多项式拟合 多项式拟合是利用次数不超过 n 的多项式来逼近给定的数据点。对于数据点 (x_i, y_i)，目标是找到一个 n 次多项式 f(x) = p_n(x) + p_{n-1}(x) + ... + p_1(x) + p_0，其中 p_k 是 x 的 k 次幂的系数，使得误差平方和最小。 当 n=1 时，多项式拟合简化为线性拟合，即直线拟合。对于一般情况，我们可以将拟合问题转化为求解多元函数的极值问题。通过建立多元函数的偏导数为零的条件，可以得到一组关于多项式系数的线性方程组，即正规方程组（法方程组）： \[ \sum_{i=0}^{m}x_i^k y_i = \sum_{i=0}^{m}x_i^k p_j(x_i), \quad j=0,1,...,n \] 这个方程组的系数矩阵是对称正定的，因此存在唯一的解。解出这个方程组，就可以得到拟合多项式 p_n(x) 至 p_0(x) 的系数，从而构建出拟合多项式 f(x)。 三、最小二乘拟合多项式的平方误差 拟合多项式 f(x) 的平方误差定义为所有数据点误差平方的平均值，表示为： \[ \bar{E} = \frac{1}{m+1}\sum_{i=0}^{m}(f(x_i) - y_i)^2 \] 平方误差提供了评估拟合质量的指标，越小说明拟合效果越好。 总结来说，最小二乘法通过最小化误差平方和来确定最佳拟合曲线，尤其在多项式拟合中，通过解决正规方程组找到拟合多项式的系数，从而实现对数据的精确描述。这种方法在数据分析、工程建模等领域有着广泛的应用。