ID3算法详解：从熵到信息增益

"ID3算法是一种用于分类的决策树算法，它通过计算信息增益来选择最佳属性进行划分。该算法基于熵的概念，熵是用来衡量数据集合纯度的统计特性。ID3算法首先计算整个样本集的熵，然后通过计算每个属性分割后的条件熵，找出信息增益最大的属性作为分裂节点。信息增益是熵减少的程度，表示选择该属性进行划分时能提供的分类信息。 在ID3算法中，熵的计算公式为：Entropy(S) = Σ-p(I)log2p(I)，其中p(I)是属于类I的样本在S中的比例，C是类别总数。当所有样本属于同一类别时，熵为0，表示数据已经完全分类；反之，若样本均匀分布，熵接近1，表示数据完全随机。 条件熵Entropy(S, A)计算的是属性A在样本集S上的熵，它是通过计算属性A所有可能值v的子集Sv的熵并加权平均得到的：Entropy(S, A) = Σ(|Sv|/|S|) * Entropy(Sv)。|Sv|表示子集Sv的样本数量，|S|表示样本集S的总样本数。 信息增益Gain(S, A)是熵减少的度量，公式为：Gain(S, A) = Entropy(S) - Entropy(S, A)。信息增益越大，表明属性A对于分类的贡献越大。ID3算法会选择信息增益最高的属性作为决策树的下一个分支。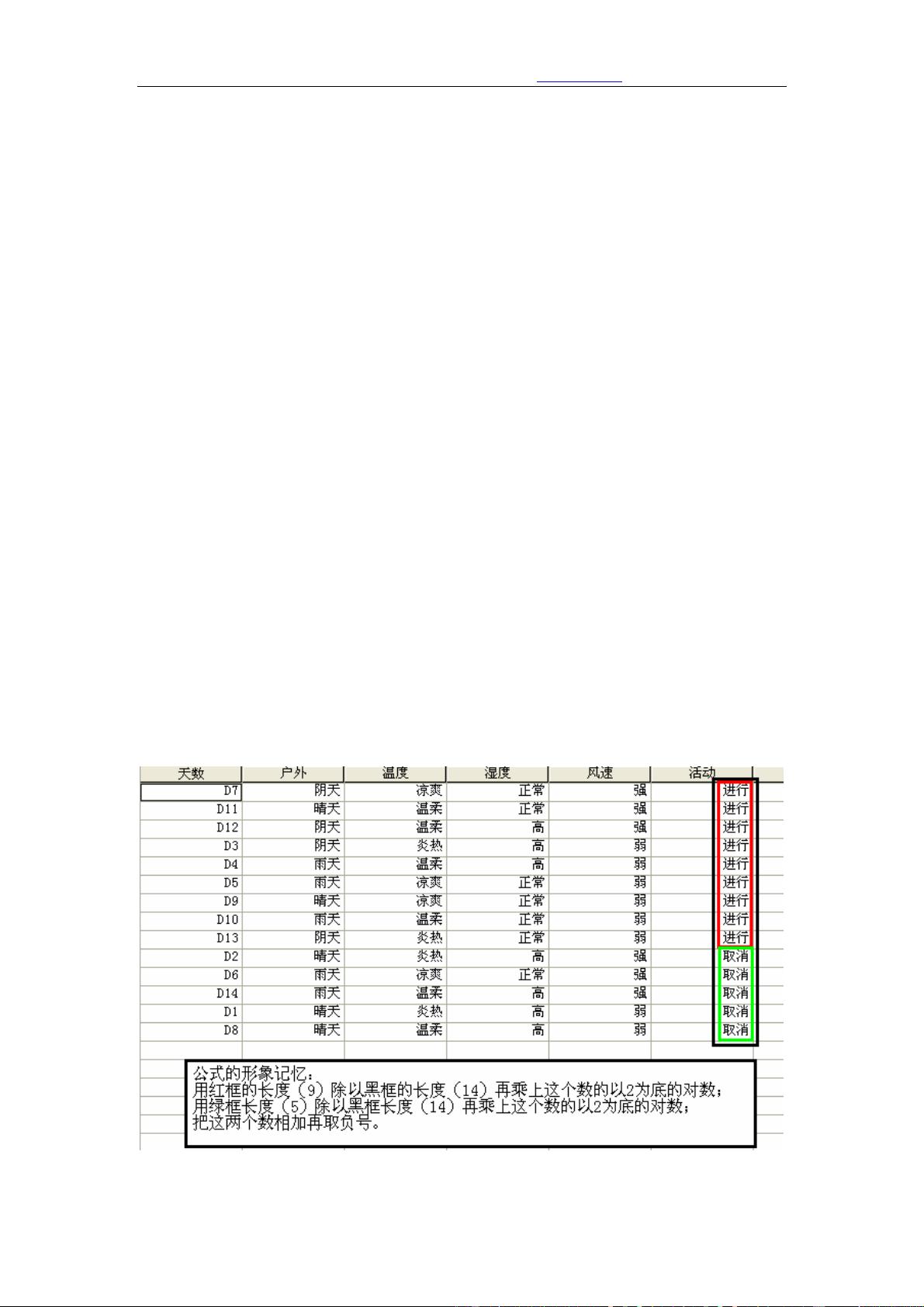 以一个简单的例子来说明，假设我们要根据天气情况判断是否适合打垒球。数据集包含14天的记录，有两个类别（可以或不可以打垒球），四个属性（户外、温度、湿度和风速）。每个属性都有多个可能的值。ID3算法会遍历所有属性，计算信息增益，然后选择信息增益最大的属性作为决策树的第一个节点，以此类推，构建出完整的决策树。 这个例子中，ID3会首先计算所有14天数据的整体熵，然后分别计算每个天气属性（户外、温度、湿度和风速）分割后的条件熵，进而计算信息增益。选择信息增益最大的属性作为决策树的根节点，接着对每个分支继续这个过程，直到所有数据被正确分类或者没有更多的属性可以分割为止。 总结来说，ID3算法是一种基于信息论的决策树构建方法，它通过比较属性的信息增益来确定最佳划分，从而生成一个能够有效分类数据的决策树模型。虽然在处理连续属性和大规模数据集时效率较低，但其直观的决策规则和易于理解的结构使得ID3成为机器学习领域经典的基础算法之一。"