二叉树与哈夫曼树详解：概念、遍历与应用

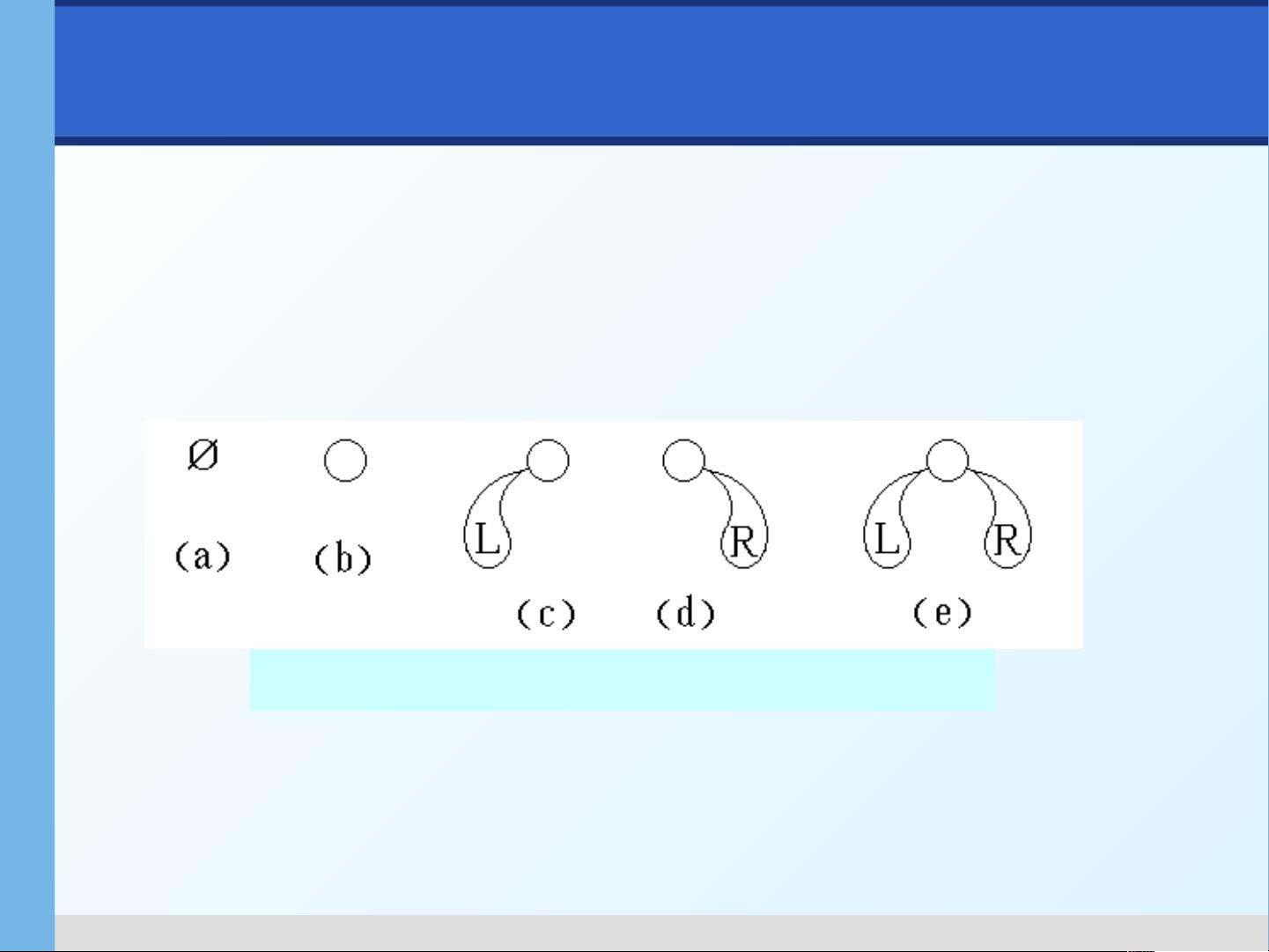
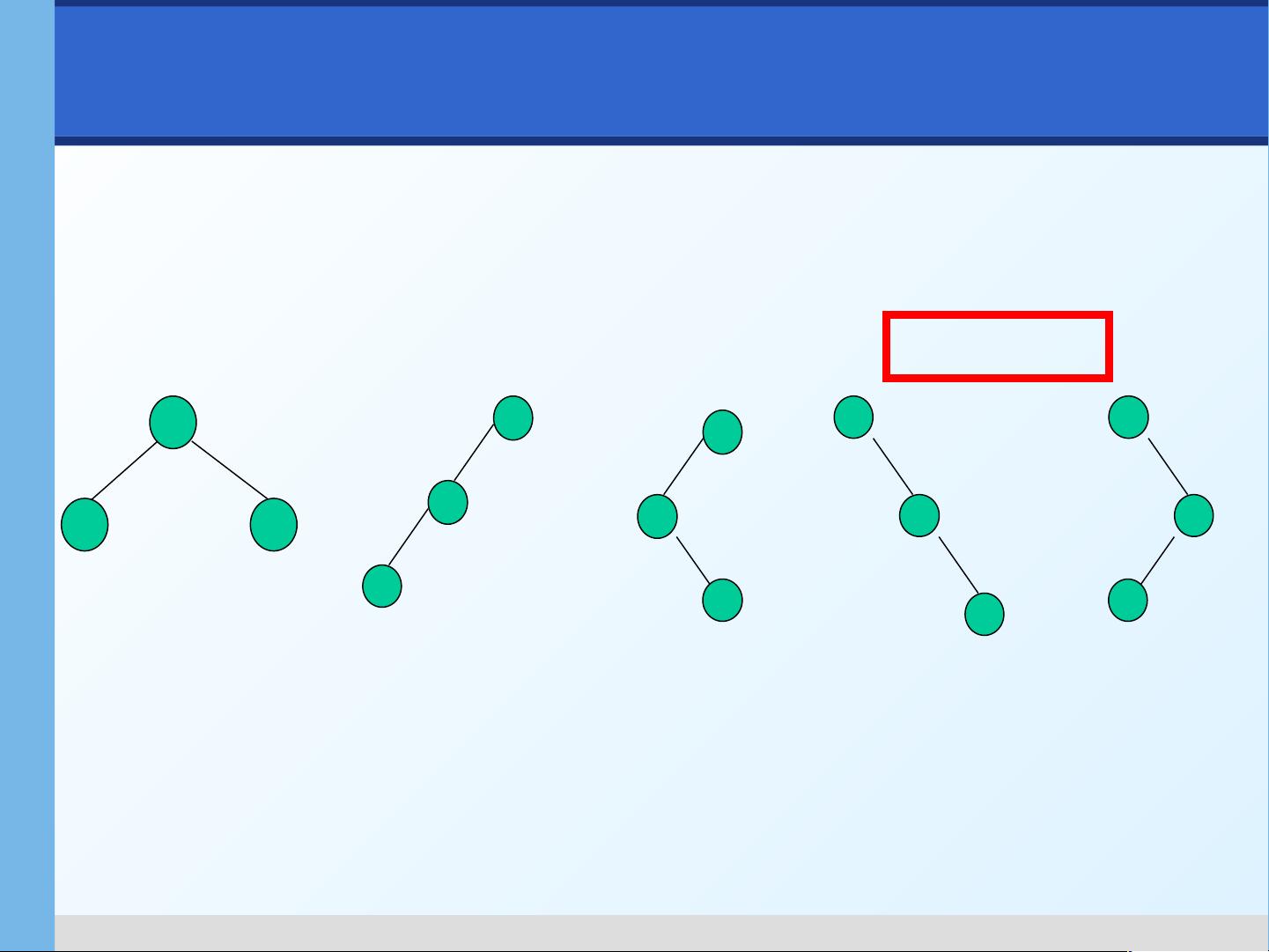
"本资源为数据结构相关的教学材料，主要讲解了树和二叉树的相关概念，包括定义、性质、存储结构以及遍历方法。重点介绍了二叉树的前、中、后序遍历，线索化二叉树，哈夫曼树的构建和应用。此外，还涉及了森林与二叉树的转换以及树的遍历方法。" 在数据结构中，树是一种重要的抽象数据类型，它由若干个节点组成，每个节点可以有零个或多个子节点。树的根节点没有父节点，而其他节点有一个父节点，多个子节点之间互不相交。树的高度表示为从根节点到最远叶节点的最长路径上的边数，树的深度则是所有节点层数的最大值。节点的度指的是该节点的子节点数量，而树的度则是所有节点度的最大值。 二叉树是树的一个特殊类型，每个节点最多有两个子节点，分为左子节点和右子节点，这种结构使得二叉树在很多操作上比普通树更有效率。二叉树的遍历方式有三种：前序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根）。线索二叉树是一种特殊形式的二叉树，通过添加线索（指向其前驱和后继节点的指针），可以在O(1)时间内查找任意节点的前驱和后继，增强了二叉树的遍历能力。 哈夫曼树，也称为最优二叉树，是一种带权路径长度最短的二叉树，常用于数据压缩。构造哈夫曼树的过程包括合并最小的两个权值节点直至只剩一个根节点，这个过程也称为哈夫曼编码。哈夫曼编码是每个字符对应的唯一二进制码，码长与字符出现频率成反比，高频字符编码短，低频字符编码长，从而达到高效压缩的目的。 森林是由多棵树构成的集合，森林与二叉树之间的转换是数据结构中的一个重要话题。通常，一棵树可以通过将其根节点作为二叉树的左子节点，其子树转换为二叉树并连接为右子节点来转换为二叉树。反之，二叉树也可以通过删除所有右子节点并重新排列左子树来转换为森林。 本教学资料旨在帮助学习者掌握树和二叉树的基础知识，包括它们的定义、性质、遍历方法以及在实际问题中的应用，如数据压缩。通过深入理解和实践这些概念，能够提升解决复杂算法问题的能力。