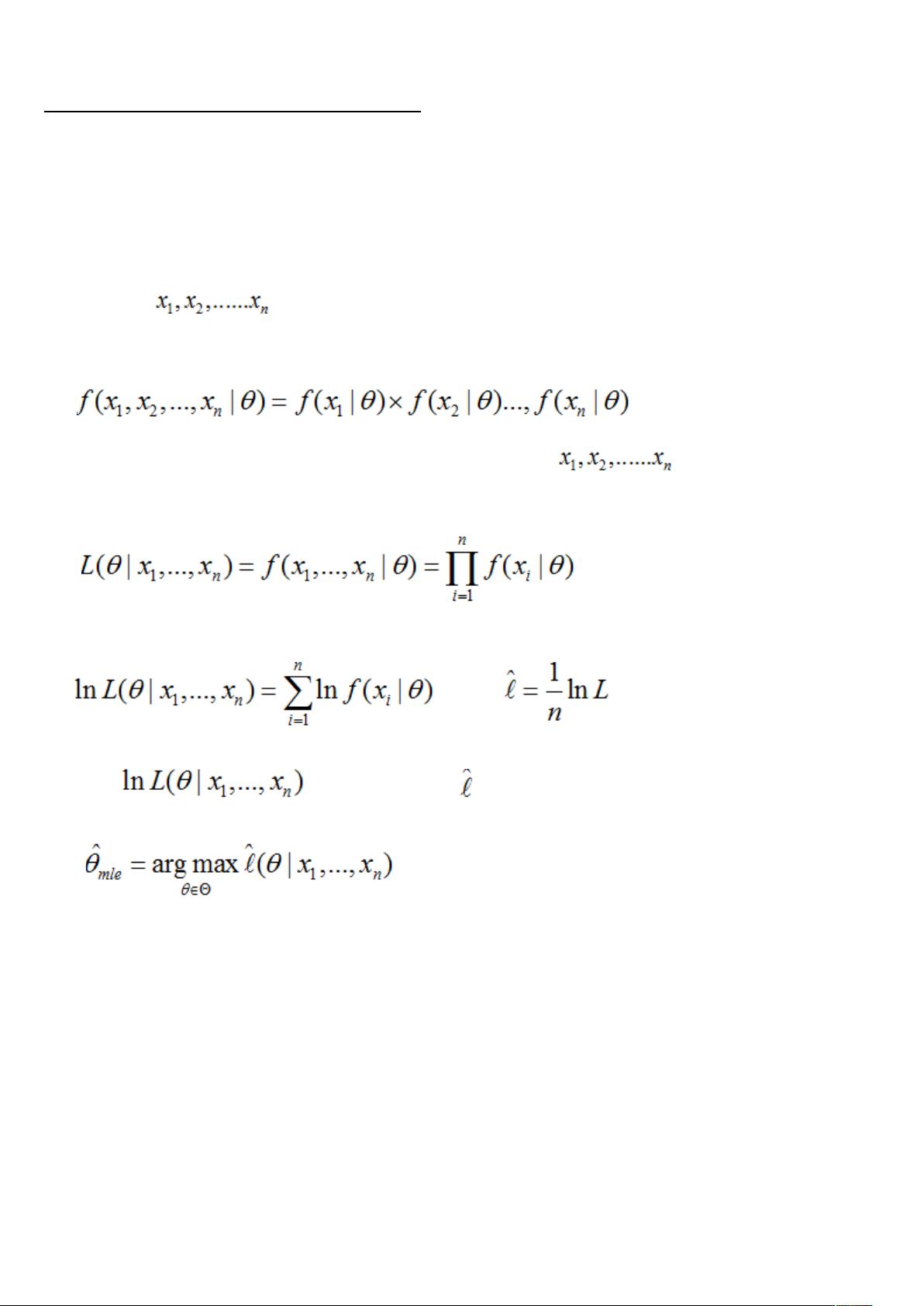最大似然估计与最大验后估计解析

"最大似然估计与最大验后估计是两种在统计学和机器学习中用于参数估计的重要方法。本文将详细介绍这两种方法，并通过实例进行解释。 最大似然估计（Maximum Likelihood Estimation, MLE）是一种基于观察数据来确定模型参数的常见技术。在MLE中，我们假设有一个模型，但模型的参数未知。例如，如果我们想估计全国人口的身高分布，可以假设身高服从正态分布，但不知道具体的均值和方差。通过采样一部分人的身高，我们可以使用最大似然估计来估计正态分布的均值和方差。关键假设是所有采样都是独立同分布的。 具体来说，设我们有独立同分布的样本集X = {x1, x2, ..., xn}，模型f依赖于参数θ，最大似然估计就是找到使样本集出现概率最大的参数θ。似然函数L(θ|X)定义为在给定参数θ下，样本集X出现的概率，即L(θ|X) = f(x1; θ)f(x2; θ)...f(xn; θ)。在实际计算中，通常取对数似然函数log L(θ|X)来简化优化过程，因为对数函数是非负且单调增加的。最大化对数似然等价于最大化平均对数似然，即求解使得E[log L(θ|X)]最大的θ，这被称为最大对数似然估计。 以黑白球比例的例子来说明，假设罐中有一定数量的黑白球，比例未知。我们多次抽取并记录球的颜色，每次抽取后球放回，形成独立同分布的样本。如果100次抽取中有70次是白球，我们想要估计白球的比例p。根据最大似然估计，我们寻找使得样本出现概率最大的p，即最大化P(Data|M)，其中Data是抽取的结果，M是模型（每次抽到白球的概率为p）。计算这个概率时，我们考虑每次抽取的独立性，将所有抽取结果的概率乘起来。 最大验后估计（Maximum A Posteriori, MAP）是最大似然估计的一种扩展，它考虑了先验知识。在MAP中，除了似然函数外，还包括了参数的先验概率分布。假设参数θ有先验概率分布π(θ)，那么MAP估计是找到使得后验概率P(θ|Data)最大的θ，即： \[ \hat{\theta}_{MAP} = \arg\max_{\theta} P(\theta|Data) = \arg\max_{\theta} \frac{P(Data|\theta) \cdot \pi(\theta)}{P(Data)} \] 其中P(Data)是归一化常数，不影响θ的选择。因此，MAP估计实际上是最大化似然函数与先验概率的乘积。 总结来说，最大似然估计只依赖于观察数据，而最大验后估计则结合了先验信息。在实际应用中，两者都是估计模型参数的重要工具，选择哪种方法取决于我们是否有可用的先验信息以及如何权衡先验与数据的重要性。"