有限域上的椭圆曲线密码体制-ECC详解

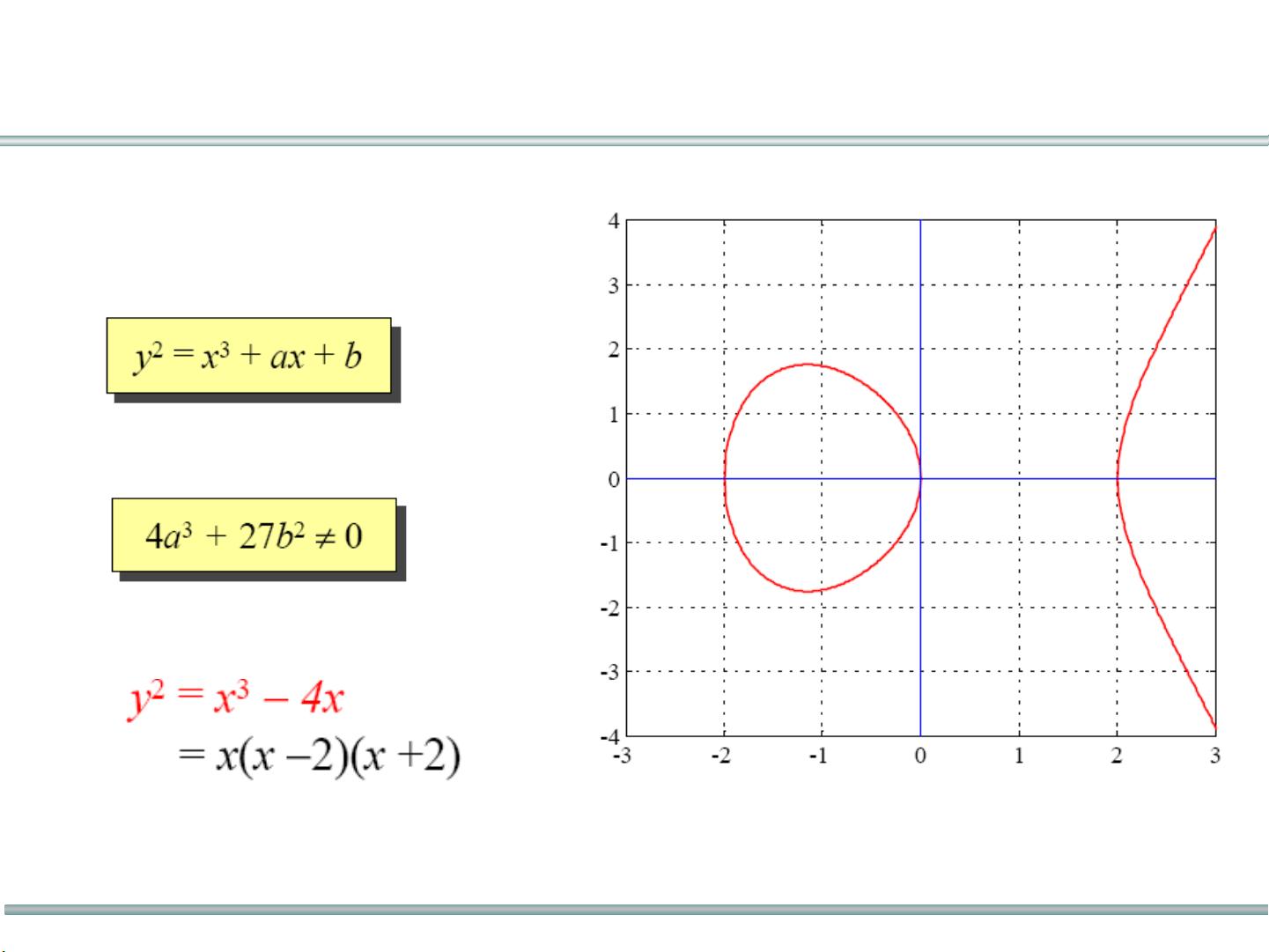
"该资源是关于有限域上椭圆曲线密码学（ECC）的课件，涵盖了椭圆曲线的基本概念、ECC的发展历史、相关标准以及其在密码学中的优势。ECC是一种基于椭圆曲线数学的加密技术，与RSA相比，它能提供相同级别的安全性但使用更短的密钥。椭圆曲线在数学上由韦尔斯特拉斯方程定义，并且在密码学中通常定义在有限域上，如GF(p)。ECC还涉及群、环和域的概念，这些是理解其数学基础的关键。" 在密码学中，有限域上的椭圆曲线（ECC）是一种重要的公钥加密算法，其理论基础源于代数几何。椭圆曲线的定义是一个二次方程的形式，即`y^2 = x^3 + ax + b (mod p)`，其中`a`和`b`是有限域GF(p)内的元素，`p`是一个大素数，且满足特定条件以确保曲线的非奇异性。这种特殊的曲线形式在密码学中有着广泛的应用，因为它提供了丰富的数学结构，能够用于构建安全的加密和签名方案。 ECC的概念由N. Koblitz和V. S. Miller在1985年分别提出，作为公钥密码体制的一种替代方案。传统的RSA加密系统需要较长的密钥来保证安全，而ECC则能在保持相同安全强度的情况下使用更短的密钥，这在计算资源有限的环境中尤其有利。例如，一个RSA需要1024位的密钥，而相应的ECC可能只需要160位，这意味着ECC在效率上有显著优势。 ECC的相关标准包括IEEE P1363, P1363a, ANSI X9.62, X9.63以及ISO/IEC 14888等，它们为ECC的实施和应用提供了框架。随着时间的推移，ECC已经从理论研究进入实际应用阶段，许多国家和公司都进行了实现和部署。 椭圆曲线的数学特性使得它们可以构造出群结构。群是一个集合，其中定义了一个二元运算，满足封闭性、结合律、存在单位元以及每个元素都有逆元。在椭圆曲线上，这个运算通常是点的加法，它允许两个点或一个点和无穷远点进行组合，得到一个新的点。这种群结构是ECC的核心，因为它允许对密钥进行操作并实现加密和解密过程。 在更深层次的数学背景下，椭圆曲线也可以被看作是环和域的一部分。环是具有加法和乘法运算的集合，而域除了环的性质外，还需要乘法运算满足交换性和存在乘法逆元。这些概念是理解ECC中如何利用椭圆曲线的结构来构建安全加密算法的基础。 有限域上的椭圆曲线密码学是一种高效且安全的加密方法，它的出现极大地推动了密码学领域的发展，尤其在物联网设备和移动通信等对计算资源要求严格的场景中，ECC的使用显得尤为重要。