椭圆曲线密码学(ECC)详解：概念、优势与应用

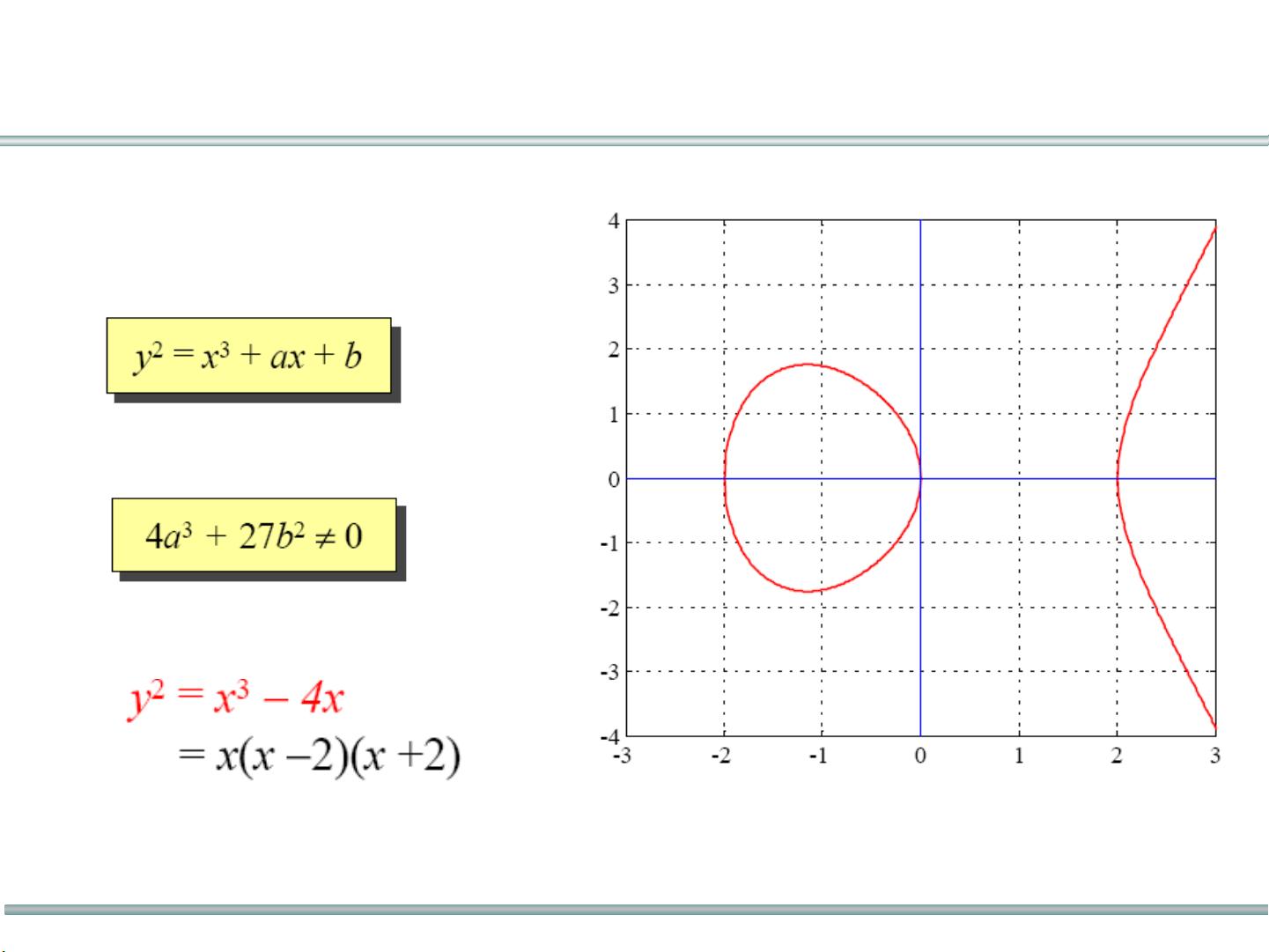
"ECC示例续-ECC相关课件" 本文主要介绍的是椭圆曲线密码学（ECC，Elliptic Curve Cryptography）的相关知识，这是一种基于椭圆曲线数学的加密技术。ECC在1985年由N.Koblitz和V.S.Miller分别提出，并逐渐发展成为一种重要的公钥加密体制，相关的标准文档包括IEEEP1363、P1363a、ANSIX9.62、X9.63以及ISO/IEC14888等。 与传统的RSA加密相比，ECC的一个显著优势在于它能提供相同安全级别但所需的密钥长度更短，这大大减少了存储和计算的需求。例如，为了达到与1024位RSA相当的安全性，ECC仅需210位的密钥，使得ECC在资源有限的设备上更具实用性。目前，许多国家和公司已经实现了ECC技术。 椭圆曲线是通过韦尔斯特拉斯（Weierstrass）方程定义的平面几何形状，该方程中的系数定义在一个基域K上，通常在有限域上使用。椭圆曲线并非我们通常理解的椭圆形，它们是由特定数学关系定义的一类曲线。 群论的概念在ECC中起着核心作用。群是一个集合，其中定义了一个二元运算，满足封闭性、结合率、存在单位元以及每个元素都有逆元。在椭圆曲线密码体制中，这些性质体现在曲线上的点集，这些点可以通过特定的加法操作进行组合，形成一个群结构。例如，示例中的点P、Q可以通过加法运算得到新的点，如P+Q或2P。 椭圆曲线上的加法操作并不直观，不同于常规的几何加法。两个点的加法可能涉及到对称轴反射，或者在某些情况下，当两个相同的点相加时，结果是曲线的无穷远点O。例如，ECC示例中展示了点P和O的加法，以及点P的双倍（2P）。 此外，环和域的概念也在此处提及。环是一个集合，其中定义了两个二元运算（加法和乘法），满足特定的代数性质。域是在环的基础上进一步要求每个非零元素都有乘法逆元的结构。 ECC利用椭圆曲线上的群结构和代数特性，构建了一种高效且安全的加密方法，广泛应用于现代网络安全、数字签名和身份验证等领域。随着技术的发展，ECC的重要性将持续增长，尤其是在物联网设备和移动通信等对资源要求严格的场景中。