椭圆曲线密码学(ECC)与点加运算

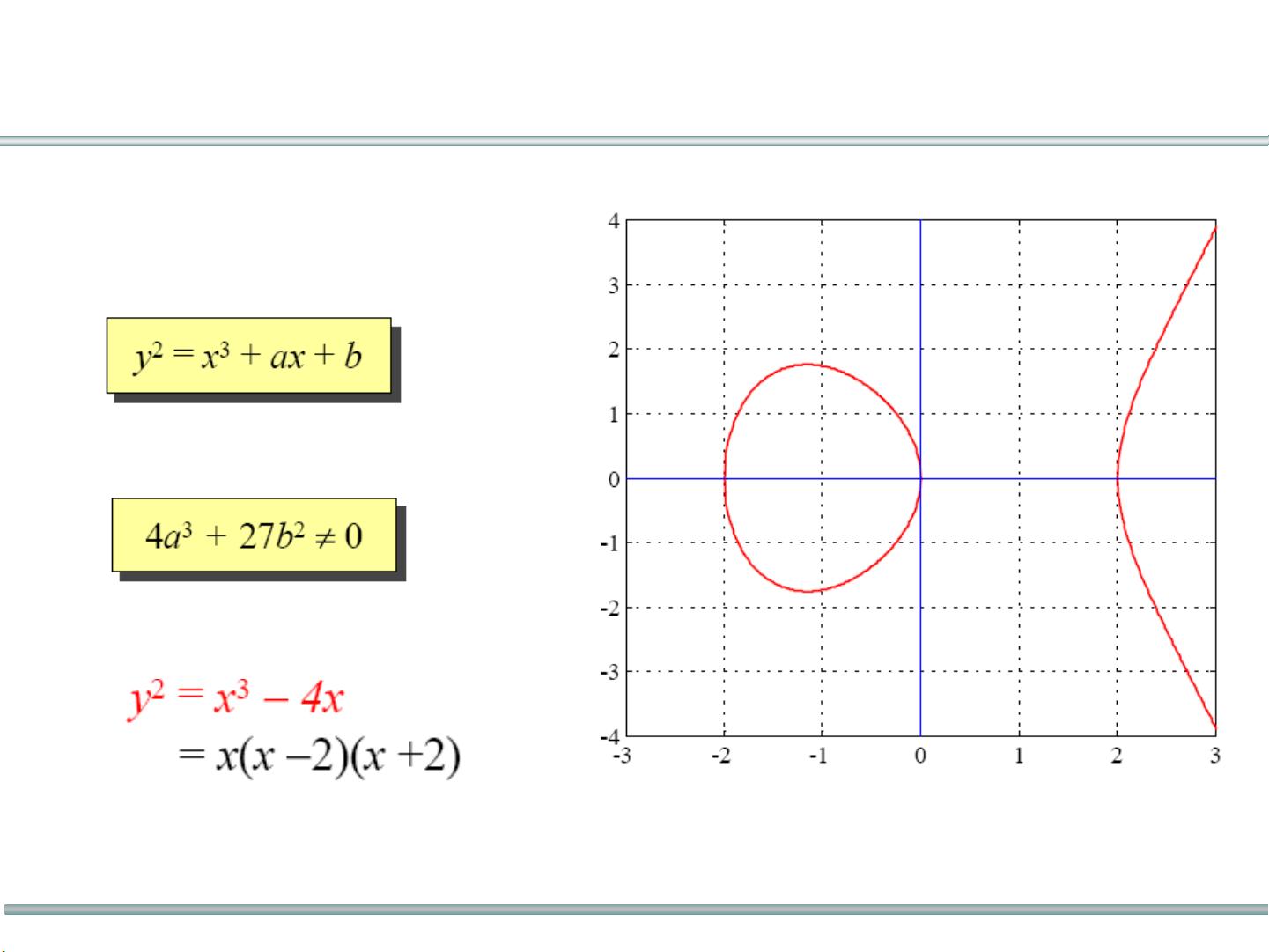
"椭圆曲线点加运算-ECC相关课件" 本文主要介绍的是椭圆曲线密码学（ECC）中的核心概念——椭圆曲线点的加法运算，以及该技术的发展和优势。椭圆曲线密码体制自1985年由N.Koblitz和V.S.Miller提出后，已成为一种重要的公钥加密技术，并被多个国际标准组织如IEEE、ANSI、ISO等制定相关标准。ECC由于其高效性和安全性，已在多个国家和公司的实际应用中得到广泛采用。 椭圆曲线（Elliptic Curve Cryptography, ECC）的核心是利用椭圆曲线上的数学性质来构建加密算法。椭圆曲线是一类由韦尔斯特拉斯方程定义的几何对象，通常形式为y^2 = x^3 + ax + b，其中系数a和b在特定的域（如有限域GF(11)）上取值。这里的例子中，曲线方程为y^2 = x^3 + x + 6 mod 11，且我们关注点(2, 4)的加法运算。 在椭圆曲线上，点的加法运算是通过特定规则进行的，即使得两个点P和Q相加得到新的点R。在这个例子中，我们展示了如何进行点的自加运算，例如2P=P+P和3P=P+P+P。这种运算在有限域GF(11)上进行，意味着所有的计算都限制在11的整数倍范围内。 椭圆曲线上的点加法构成一个群结构，具有封闭性、结合律、单位元（无穷远点）和逆元（每个非无穷远点都有一个逆元，即与之相加得到无穷远点的点）。群论的概念在这里至关重要，因为它是理解椭圆曲线加密算法的基础。群的这些特性使得椭圆曲线上的点加法运算能够形成一个安全且可预测的数学模型。 相比传统的RSA加密体制，ECC的主要优势在于其更高的效率和安全性。尽管RSA的安全性依赖于大素数分解的难度，但随着计算能力的提升，所需密钥长度也不断增长，导致加密和解密过程耗时较长。而ECC则可以在较短的密钥长度下提供相同的加密强度，这降低了存储和计算的需求，使得ECC在资源受限的设备中特别有用。 例如，为了达到相同的安全水平，ECC的密钥可能只有RSA密钥长度的五分之一至十分之一。这种效率差异使得ECC在物联网设备、移动通信和区块链技术等领域成为理想的加密选择。 总结来说，ECC是一种利用椭圆曲线上的群论性质设计的密码系统，它提供了与RSA等传统方法相比更高效、更安全的加密手段。通过对椭圆曲线上的点进行加法运算，ECC能够实现安全的数据加密，且在有限域内进行的运算确保了计算的可行性。随着技术的发展，ECC的应用越来越广泛，成为现代信息安全领域不可或缺的一部分。