离散信号处理:冲激响应与系统分析示例
需积分: 3 11 浏览量
更新于2024-09-09
收藏 137KB DOC 举报
数字信号处理是一门研究如何将连续时间信号转换成离散时间信号,并对其进行分析、加工和恢复的学科。在这个领域,我们通过数学模型和算法来处理电信号、音频信号和其他形式的数据。本资源提供了一系列实验内容,涵盖了离散时间系统的基础概念以及关键操作。
首先,实验一的重点是离散卷积和单位脉冲响应。函数`pr1()`展示了如何定义一个二阶差分方程,并利用`filter()`函数计算其单位脉冲响应(即系统对单位脉冲输入的响应)。通过`stem()`函数绘制了冲激响应图,观察系统对突发信号的反应。同时,使用`tf2zp()`函数将传递函数转换为零极点图,帮助理解系统的动态特性。`impseq()`函数用于创建一个特定序列。
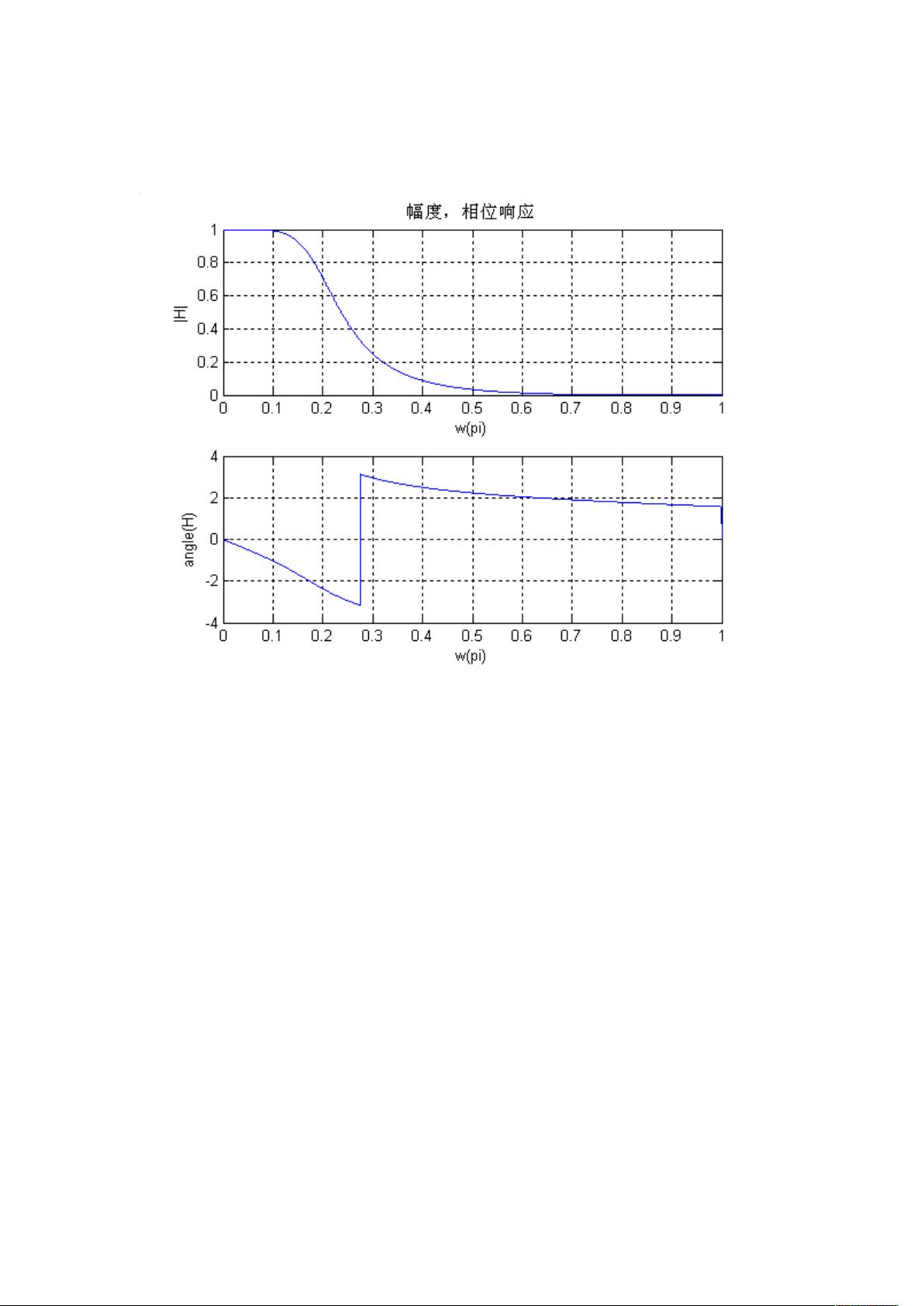
接着,实验二进一步探讨了离散系统的频率响应。通过定义一个特定的系统函数H,该函数由系数b和a确定,我们计算了系统的幅频和相频响应。`pr2()`函数中,我们使用复数指数形式表示系统函数,然后计算其模(幅度)和幅角(相位),分别绘制在两个子图中。这些分析有助于了解系统的频率响应特性,如增益和相位变化随频率的变化情况。
总体来说,这部分内容涉及了数字信号处理中的基础概念,包括离散时间系统的数学模型、卷积的概念、以及对系统性能的频域分析。这对于理解和设计数字信号处理器件、滤波器、通信系统以及音频处理等应用至关重要。通过实际编程和可视化,学生可以深入理解数字信号处理的核心原理和技术。
1329 浏览量
1299 浏览量
1470 浏览量
101 浏览量
1142 浏览量
859 浏览量
563 浏览量
126 浏览量
qq_28042291
- 粉丝: 0
- 资源: 1