Trie树与后缀树：字符串算法解析

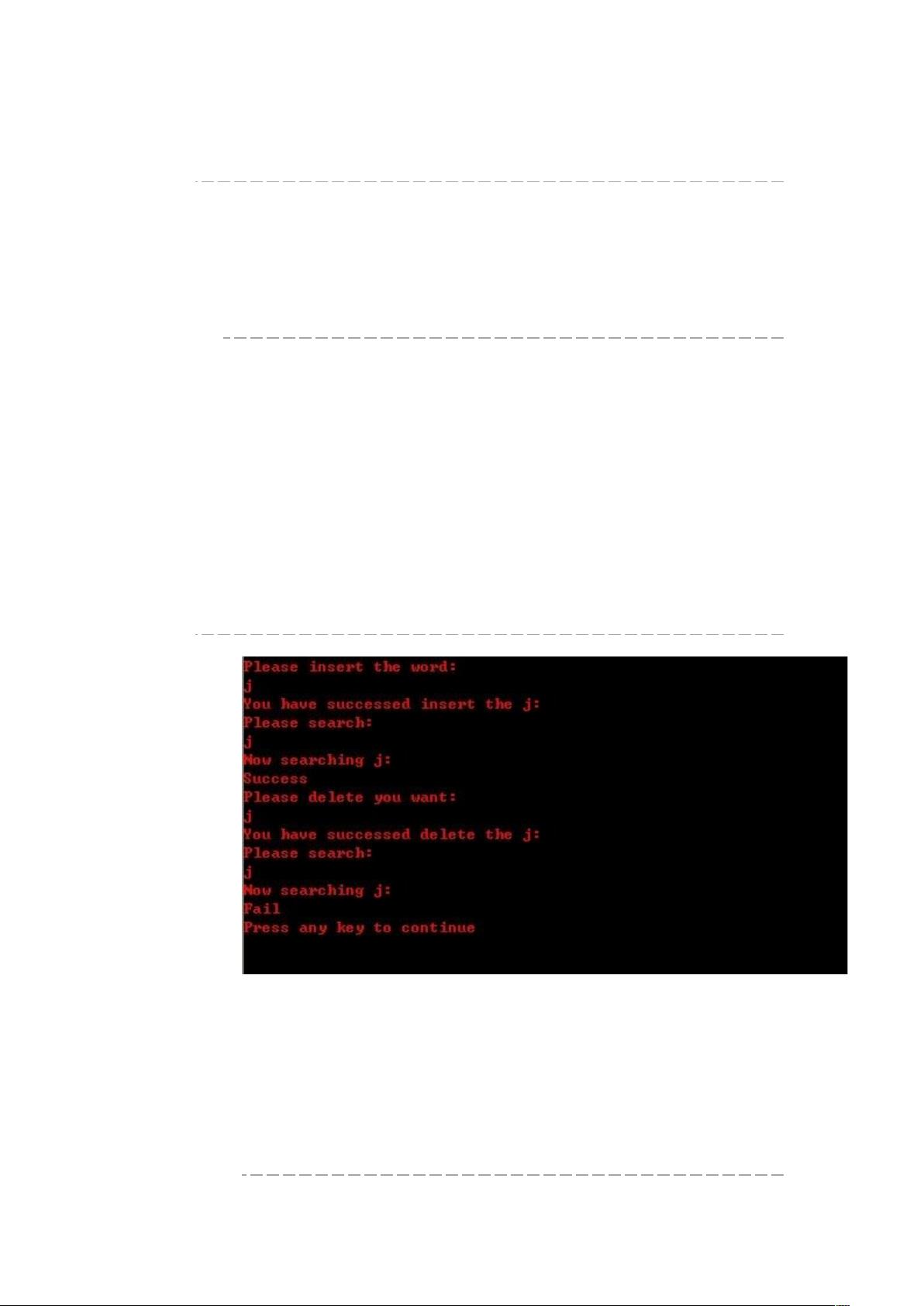
"从Trie树到后缀树的字符串匹配算法" Trie树，又称字典树或前缀树，是一种用于高效存储和检索字符串的数据结构。它通过将字符串的字符按照字典序进行展开，形成一棵树，使得每个节点代表一个字符串的前缀。在Trie树中，从根节点到任一叶子节点的路径上的边所对应的字符序列即为该叶子节点代表的字符串。这样的结构使得插入和查询操作的时间复杂度可以达到O(k)，其中k为查询字符串的长度。 对于第一个问题，利用Trie树可以有效地统计单词出现的频率。当读取文件时，将每一行的单词作为键插入Trie树，同时在节点中记录出现次数。由于Trie树的特性，同一单词的不同实例都会指向相同的节点，因此节点的计数就能反映单词的总出现次数。统计完成后，找到计数最多的10个节点即可。时间复杂度分析，构建Trie树的时间复杂度为O(n*le)，其中n为单词总数，le为单词平均长度。查找最频繁的10个词，如果使用堆，时间复杂度为O(n*lg10)。总的时间复杂度取决于两者中的较大者。 后缀树是一种更为强大的字符串数据结构，它能够存储一个字符串的所有后缀，并且每个后缀只占用一次空间。后缀树的构建通常基于Ukkonen算法或McCreight算法。在后缀树中，任何字符串S1是字符串S的子串，如果存在S的一个后缀等于S1，那么S1在后缀树上可以通过从根节点开始的某条路径表示出来。 对于第二个问题，寻找最长回文子串，后缀树是理想的工具。可以遍历后缀树，找到具有相同前缀的回文串，这些回文串的共同部分就是最长回文子串。例如，对于输入字符串"XMADAMYX"，在后缀树中可以找到"MADAM"这个回文串。 后缀树还可以解决以下问题： 1. 查询字符串S是否包含子串S1，通过在后缀树上进行查找，时间复杂度与KMP算法相当。 2. 找出字符串S的最长重复子串，通过寻找具有相同前缀的后缀，最长的那个就是最长重复子串。 3. 找出字符串S1和S2的最长公共子串，可以在S1的后缀树中查找S2的后缀，找到的最长公共部分即为最长公共子串。 4. LZW无损压缩算法，LZW利用后缀树构建动态字典，快速地为出现过的字符串分配压缩码，从而实现数据压缩。 Trie树和后缀树是字符串处理中的重要工具，它们在字符串匹配、搜索和压缩等领域有着广泛的应用。Trie树适合于统计和查找频繁项，而后缀树则更擅长解决复杂的字符串模式匹配问题。理解并熟练运用这两种数据结构，对于解决实际的字符串问题至关重要。