门爱东教授讲解：离散傅里叶变换与快速傅里叶变换

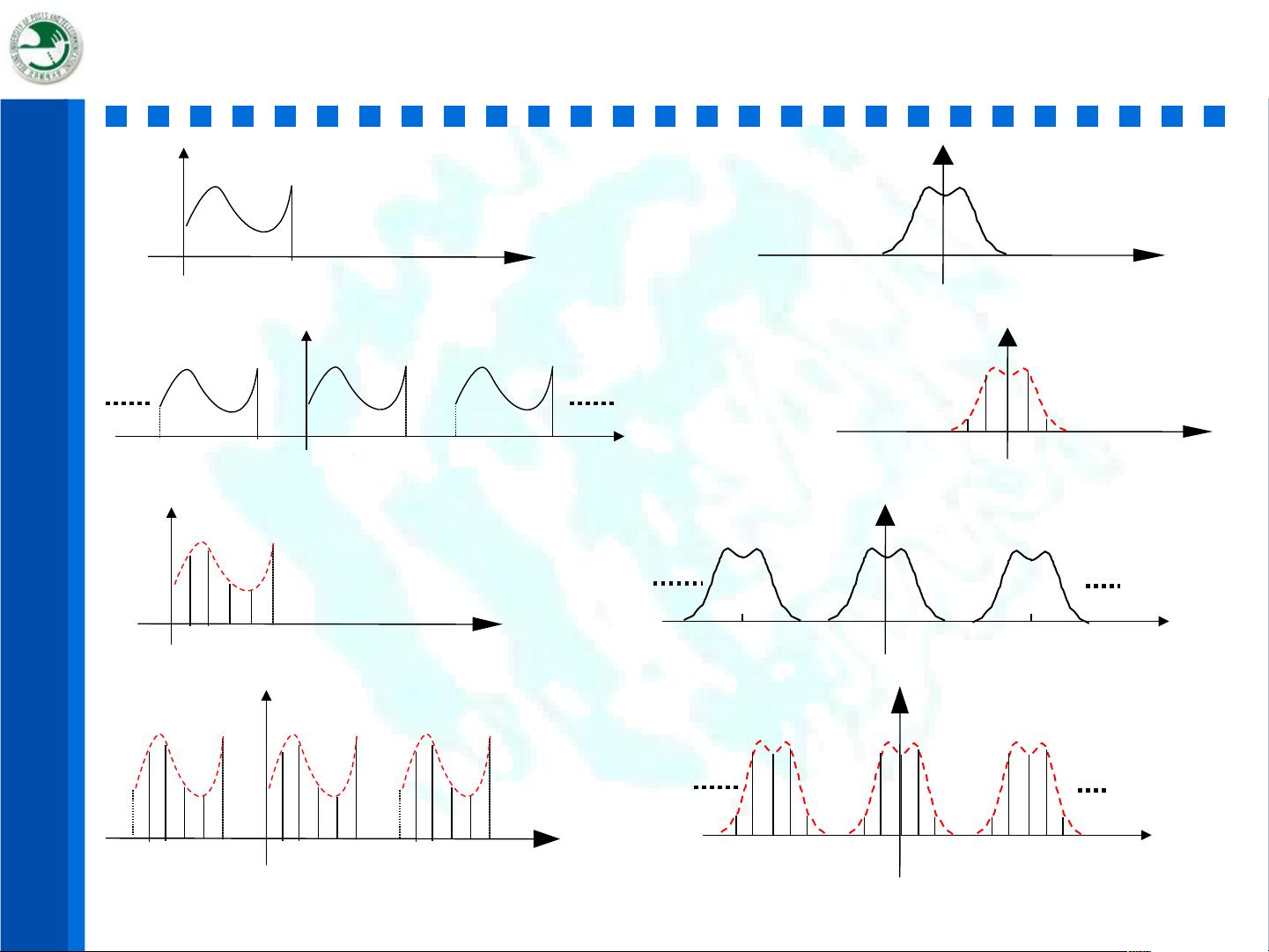
"该资源是北京邮电大学信息与通信工程学院多媒体技术中心门爱东教授的《数字信号处理》第二版的PPT，主要涵盖了离散傅里叶变换（Discrete Fourier Transform, DFT）和快速傅里叶变换（Fast Fourier Transform, FFT）的相关内容。" 在数字信号处理领域，离散傅里叶变换（DFT）和快速傅里叶变换（FFT）是至关重要的工具，用于分析和处理离散时间信号。离散傅里叶变换是一种数学工具，它将离散时间序列转换到频率域，从而揭示信号的频率成分。DFT定义为有限长序列的离散傅里叶级数（DFS），它可以表示一个离散信号在所有可能频率上的幅度和相位。 离散傅里叶变换的计算通常涉及到大量的复数乘法和加法，对于长序列来说，这个计算过程非常耗时。快速傅里叶变换正是为了解决这个问题而提出的，它通过使用分治策略和对称性来大幅减少计算量。FFT算法是DFT的一种高效实现，大大降低了计算复杂度，从O(N^2)降低到O(N log N)，使得大规模信号处理成为可能。 此外，PPT还可能涉及了Z变换，它是离散时间信号分析的另一种方法，类似于连续信号的拉普拉斯变换，但使用复变量z作为自变量，可以处理无限长序列以及稳定性和因果性的问题。 在数字信号处理的其他章节，可能会讨论IIR（无限脉冲响应）和FIR（有限脉冲响应）数字滤波器的设计和实现，这些滤波器常用于信号的频率选择性衰减或增益。数字滤波器设计通常结合离散傅里叶变换和快速傅里叶变换来完成，例如使用窗函数或频率采样方法。 最后，数字信号处理中的有限字长效应对实际系统中的量化误差进行了探讨，由于计算机内部存储和运算的限制，信号在数字化过程中不可避免地会出现精度损失，这可能会影响信号处理的结果。 门爱东教授的《数字信号处理》第二版PPT深入讲解了离散傅里叶变换和快速傅里叶变换的基本概念、计算方法以及它们在数字信号处理中的应用，是学习和理解数字信号处理理论与实践的重要参考资料。