机械系统数字控制入门：应用导向教程

需积分: 10 88 浏览量更新于2024-07-17 收藏 1.08MB PDF 举报

"《应用数字控制入门》第二版是机械工程领域为高级或初级研究生提供的一本关于机械系统数字控制的教材，特别强调实际应用。作者格雷戈里·S·斯特拉在编写本书时，对现有的数字控制教科书感到不满，尽管它们内容详尽，但更适合于查阅而非教学指导。斯特拉认为，尽管近年来已有更多以学生为导向的新教材出现，但市场仍缺乏一本针对初学者的、更侧重实践应用的教材。书中深入浅出地讲解了数字控制系统的设计与分析，特别是如何利用MATLAB这样的工具进行实时系统建模、仿真和优化。作者强调了MATLAB在实际工程中的重要性，并提供了大量的MATLAB脚本和实例，帮助读者掌握这一关键技能。斯特拉感谢了他的家人，包括妻子安妮和四个儿子保罗、基思、马克和杰夫，他们在本书准备和修订过程中给予了极大的支持，同时他也怀念已故的父亲杜克·斯特拉，他鼓励那些热爱数学和摩托车的儿子。通过这本书，读者可以学习到如何将数字控制理论应用于机械系统的实际问题解决，包括传感器数据处理、控制器设计、系统辨识以及闭环控制系统的调试和优化。书中不仅涵盖了基本概念，还涉及现代技术趋势，如网络化控制和嵌入式系统，使得学生在进入职场后能迅速适应快速发展的数字化控制领域。《应用数字控制入门》旨在为机械工程专业学生提供一个实用且全面的学习平台，弥补了传统教材在教学实用性上的不足。"

2 CHAPTER 1. INTRODUCTION AND SCOPE OF THIS BOOK

Computer

A/D

Clock

D/A Plant

Sensor

r(t) e(t) e(kT)

u(kT) u(t)

w(t)

y(t)

v(t)

y(t)

r = reference input or setpoint

u = control force (actuator input)

y = controlled variable or output

ˆy = measurement of controlled variable

e = r − ˆy = error signal

w = disturbance acting on the plant

v = measurement noise

A/D = analog-to-digital converter

D/A = digital-to-analog converter

Figure 1.1: Basic digital control system.

1.1.2 Digital control

Digital control systems employ a computer as a fundamental component in the controller. The

computer typically receives a measurement of the controlled variable, also often receives the reference

input, and produces its output using an algorithm. This output is usually converted to an analog

signal using a D/A converter, then ampliﬁed by a power ampliﬁer to drive the plant. A block

diagram of a typical digital control system is shown in Figure 1.1.

When compared to a continuous-time system, there are three new elements in the block diagram of

Figure 1.1:

• A/D converter. This device acts on a continuous physical variable, typically a voltage, and

converts it into an integer number. A/D converters typically have unipolar ranges of 0–5 V,

0–10 V, or bipolar ranges of ± 5 V, or ± 10 V. These are often jumper-selectable. The A/D

conversion causes quantization q, given by the resolution of the converter in bits. Common

resolutions are 8 bits (256 levels), and 12 bits (4096 levels). A 12-bit A/D converter of range

±10 volts would have a conversion quantum of q = 20/4096 = 4.88 mV. Note that quantization

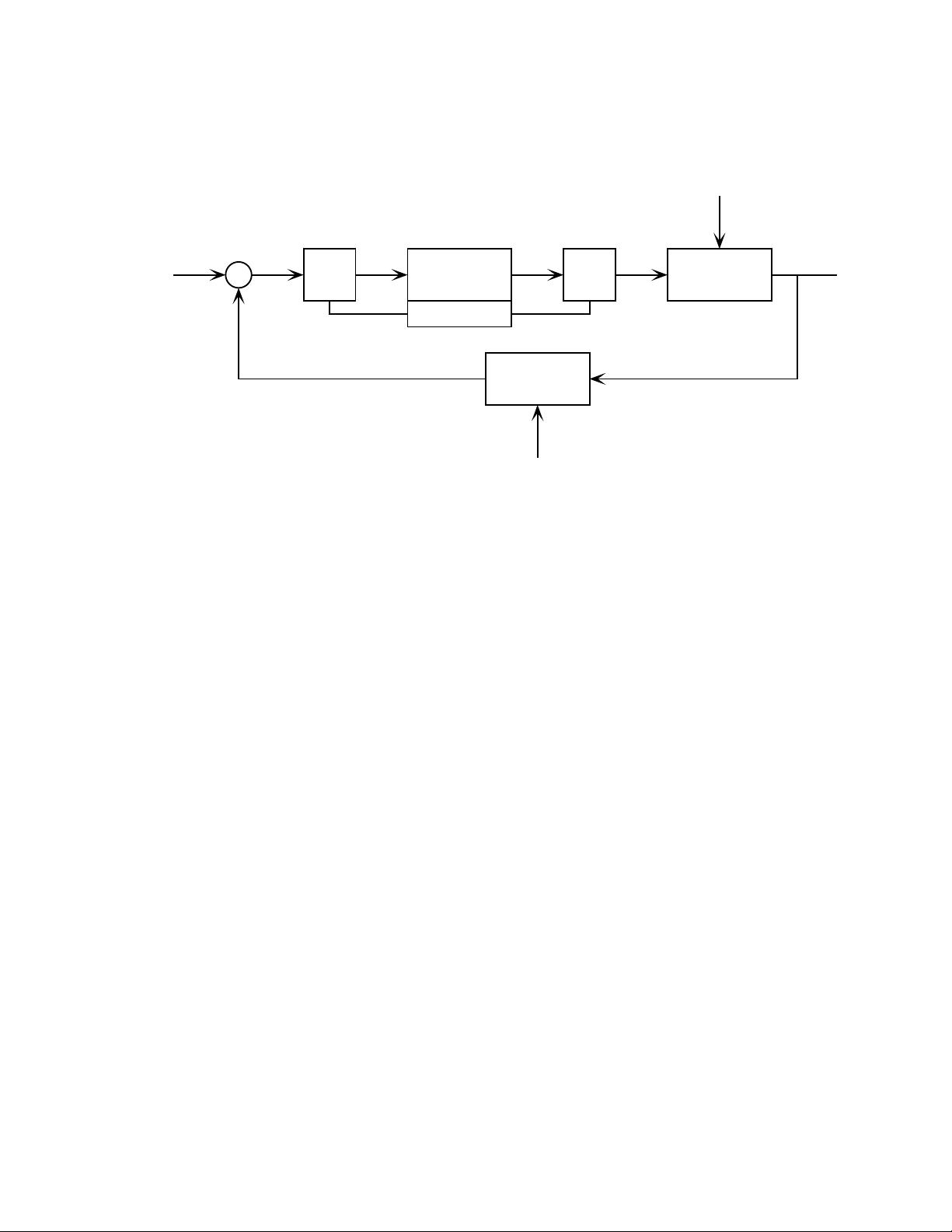
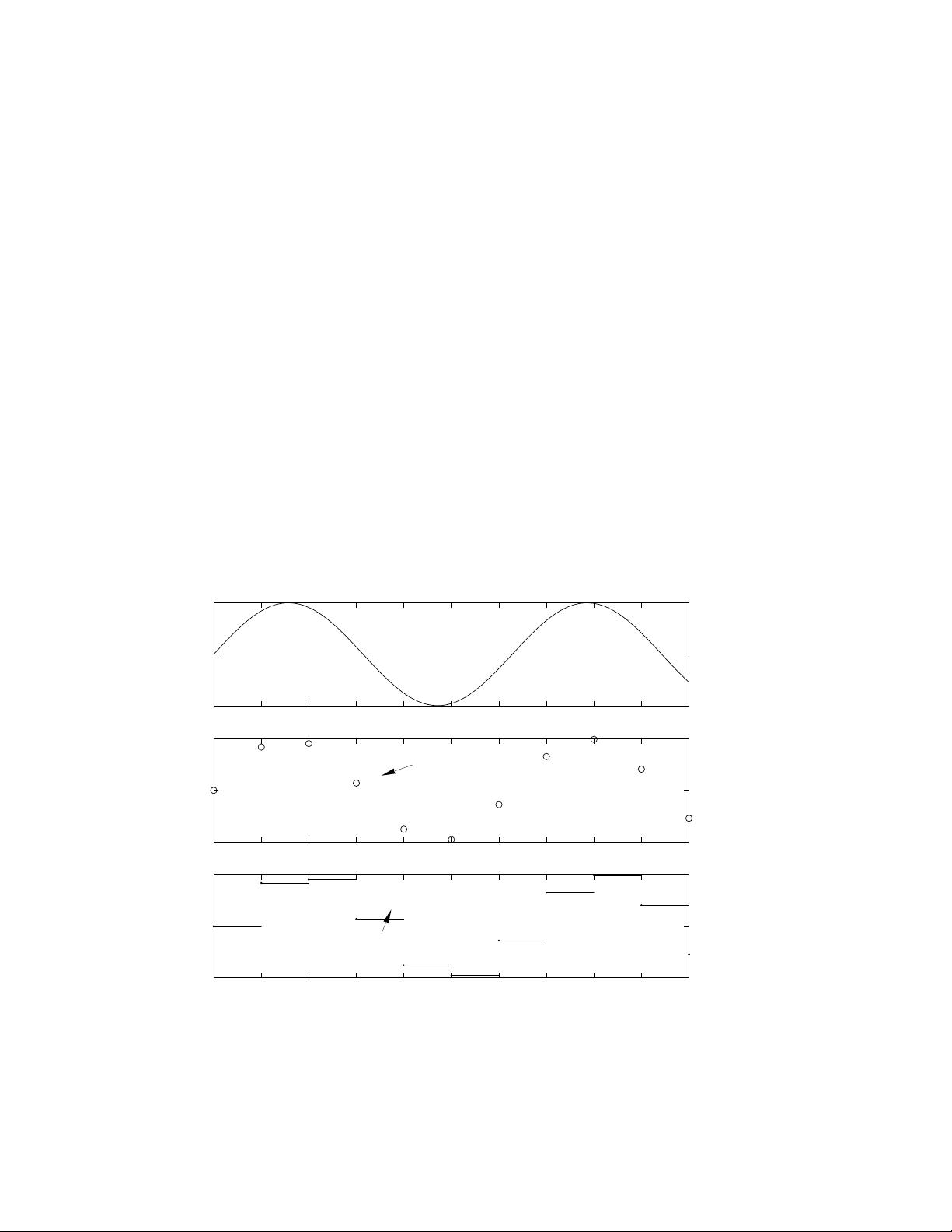
4 CHAPTER 1. INTRODUCTION AND SCOPE OF THIS BOOK

Much of the task of designing a digital controller is in accounting for the eﬀects of quantization

and sampling, especially sampling. If both T and q are small, digital signals approach continuous

signals, and continuous methods of analysis and design may be used. However, when this is not the

case, continuous methods can lead to erroneous results.

1.2 Philosophy and Text Coverage

The philosophy of this course is to present the basic material necessary for the analysis and design

of digital control systems. We assume a background in continuous systems, and relate the digital

problem to its continuous counterpart. The emphasis is on understanding the physical reality behind

the analysis.

The eight chapters in this book contain the following material:

Chapter 1. This chapter. Describes philosophy and content of book. Some deﬁnitions. Rationale

for studying digital control.

Chapter 2. Sampled (discrete-time) variables. Introduction of the z-transform for discrete vari-

ables, which is analogous to the Laplace transform for continuous variables.

Chapter 3. Discrete simulations of continuous systems. Several methods of simulation are given,

speciﬁcally numerical integration, pole-zero mapping, and zero-order hold equivalence.

Chapter 4. Frequency spectra of sampled signals. The impulse modulation model of sampling.

Aliasing and its eﬀects.

Chapter 5. Transform-based design of digital control systems, primarily using the root locus

method. When sampling can be ignored, and when it must be considered.

Chapter 6. State-space modeling and analysis of continuous systems, including nonlinear systems.

Chapter 7. State-space design of digital control systems, primarily using pole placement. Control

law design and state estimation. Introduction of the reference input.

Chapter 8. System identiﬁcation using the least squares method.

It is the author’s observation that digital control systems are so widely used that it is rare to see a

completely continuous control system. There are several reasons for this:

• Computers are getting faster, cheaper, and more reliable.

• Control systems incorporating computers are inherently more ﬂexible than those without, e.g.

during the prototyping phase, tuning gains to achieve satisfactory performance is simply a

matter of changing numbers in a computer program, rather than changing hardware.

• Advanced control techniques such as optimal and adaptive control can only be realized digitally.

剩余196页未读，继续阅读

qq_35751287

粉丝: 0
资源: 1

机械系统数字控制入门：应用导向教程

Introduction to applied mathematics

Alan Davies： An Introduction to Applied Linguistics-From Practice to Theory 2nd Edition[2007][T]

introduction to robotics mechanics and control 3rd edition

an introduction to stochastic differential equations version微盘

introduction to linear optimization pdf

introductionto3dgameprogrammingwithdirectx12 pdf

coursera introduction to power electronics free

Introduction to Linear Optimization

Introduction to Statistics Stanford University

introduction to data science

最新资源