Lattice ispMACH 4A系列：高性能可编程逻辑器件

ispMACH 4A系列是Lattice公司提供的高性能E2CMOS工艺的CPLD（复杂可编程逻辑器件）解决方案，其特点是架构灵活、易于使用且提供可靠的硅产品和软件工具。这款CPLD适用于快速逻辑设计，确保了用户在开发过程中的稳定性和效率。 ispM4A5-12864-10YI是该系列中的一员，它提供了从32到512个宏观单元的密度选择，同时实现100%的利用率和100%的引脚保留，支持5V或3.3V工作电压。这一型号的特点包括： 1. **卓越的一次到位（First-Time-Fit）和重构（re-fit）特性**：设计更改后无需重新布局，方便系统集成，确保了在设计变化后的无缝对接。 2. **速度锁定（SpeedLocking）技术**：通过使用最多20个产品术语（product terms）来驱动输出，ispM4A5能够提供高达5.0ns的典型延迟时间（tPD）和182MHz的最大频率（fCNT），从而确保了固定时序性能的稳定性。 3. **高速接口**：无论是商业级（5.0ns tPD）还是工业级（7.5ns tPD），以及182MHz的极限频率，ispM4A5表现出极高的数据传输速度。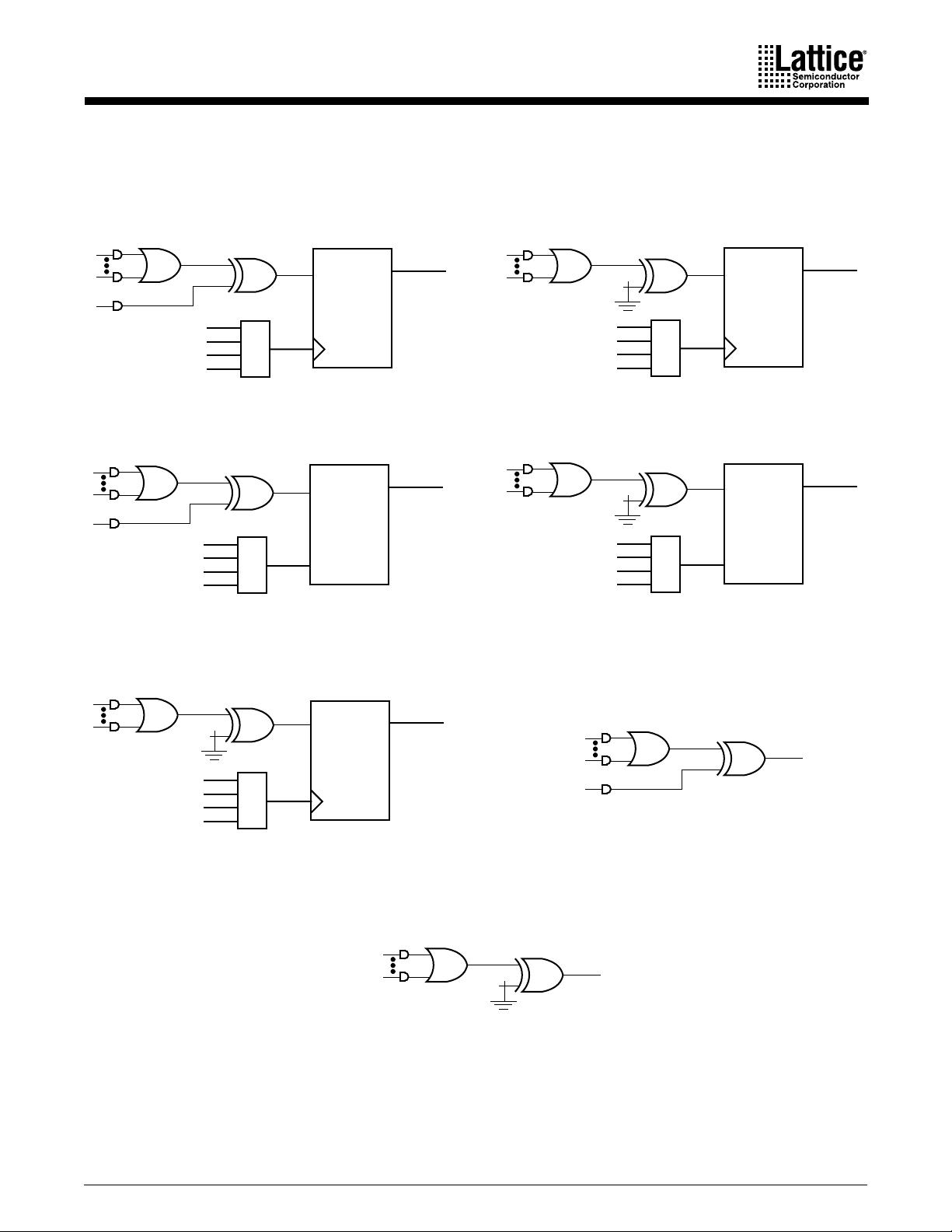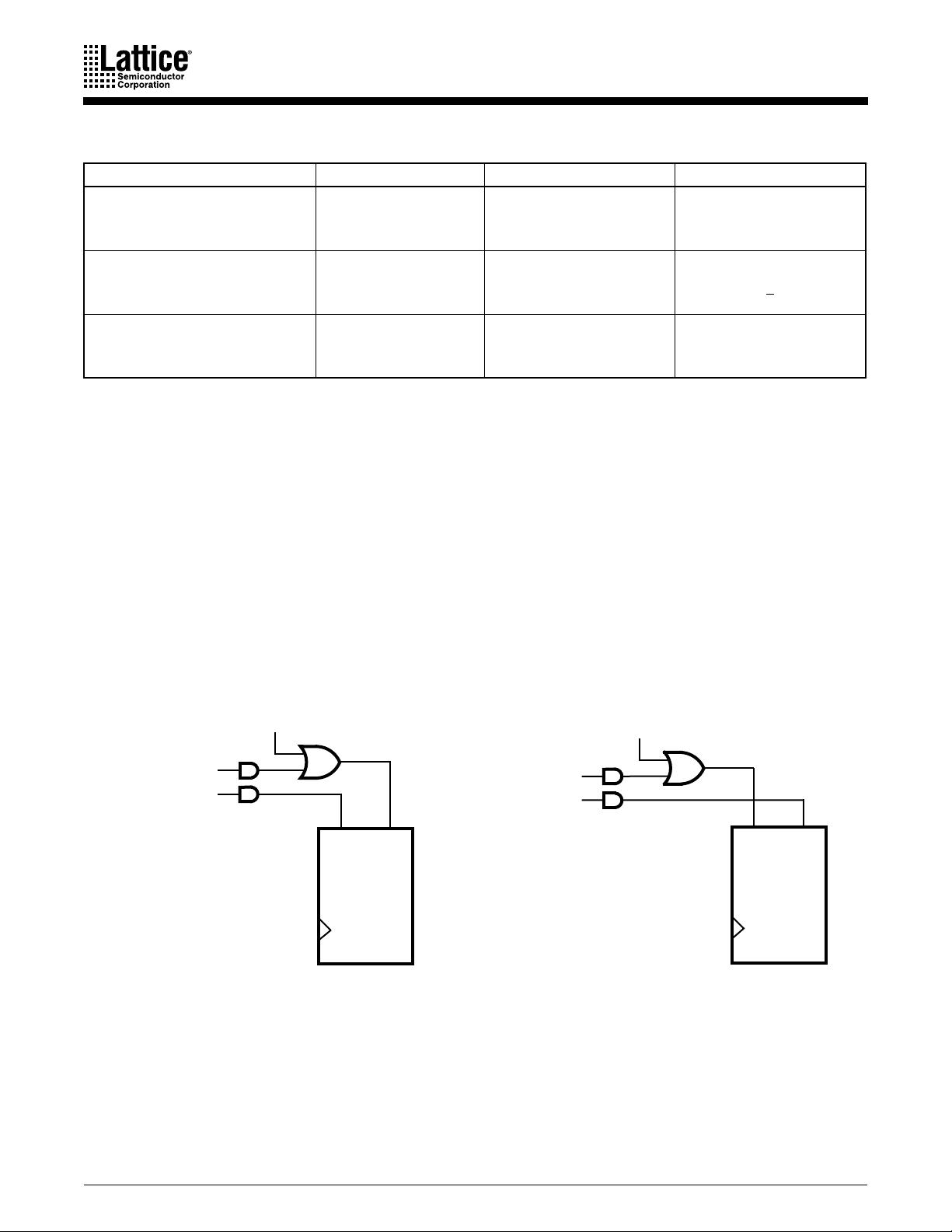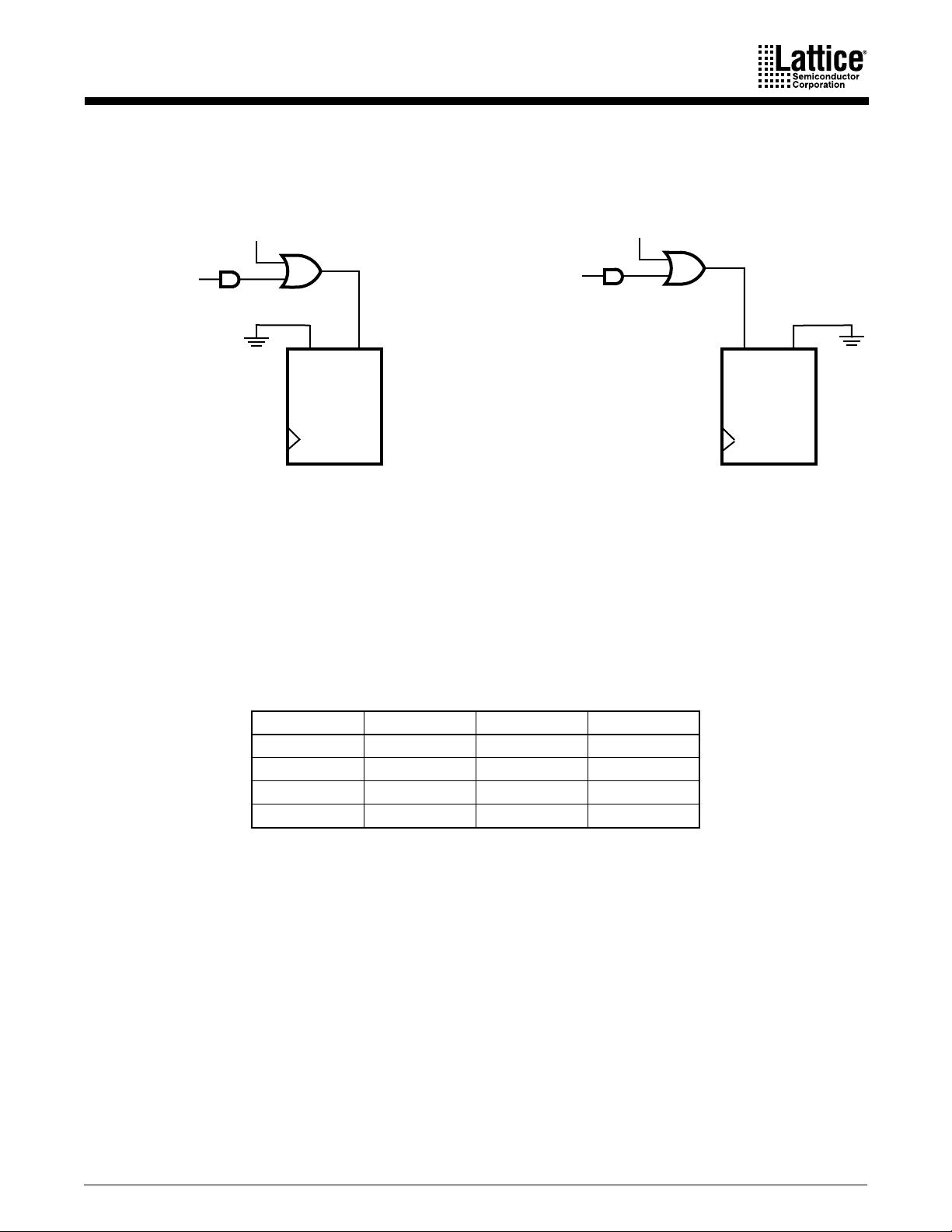 4. **丰富的功能集**：包括多样的设计风格支持，如D/T寄存器和触发器、同步或异步模式、专用输入寄存器、可编程极性、重置/预置信号交换等，提供了极大的设计灵活性。 5. **高级系统集成特性**：ispM4A5兼容3.3V和5V的JEDEC标准操作，支持JTAG（IEEE 1149.1）进行边界扫描测试，便于自动化设备的测试。此外，它还具备5V和3.3V的JTAG内系统编程能力，符合PCI标准，并能在混合供电电压系统设计中安全运行。 6. **封装选项**：ispM4A5提供多种封装类型，如PLCC、PQFP、TQFP、BGA、FBGA和cBGA，满足不同应用对引脚数和封装需求。 ispM4A5-12864-10YI是一款高度灵活且性能优越的CPLD，适合各种高性能应用，通过强大的功能和广泛的兼容性，极大地简化了用户的设计流程，降低了成本并加快了产品的上市时间。