动态规划算法详解:从概念到应用
需积分: 0 129 浏览量
更新于2024-07-01
1
收藏 9.02MB PDF 举报
"本资源主要介绍了动态规划法的学习要点,包括理解动态规划的概念,掌握其基本要素:最优子结构和重叠子问题性质,以及设计动态规划算法的步骤。此外,还对比了动态规划与分治法、贪心法的异同,并通过多个应用范例如多段图问题、最短路径、最长公共子序列、0/1背包问题、流水作业调度问题来阐述动态规划算法的设计策略。资源涵盖了动态规划的一般方法、基本要素、与分治法的区别,以及动态规划在实际问题中的应用。"
动态规划是一种解决最优化问题的有效方法,由贝尔曼等人在20世纪50年代提出。它的核心思想是将复杂问题分解为相互关联的子问题,通过解决子问题逐步构建整个问题的最优解。与分治法相似,动态规划也会将问题分解为子问题,但关键区别在于动态规划的子问题通常存在重叠,且这些子问题的解会被存储并重复利用,以避免不必要的计算,从而提高效率。
动态规划算法的基本要素包括:
1. **最优子结构**:最优解包含其子问题的最优解。这意味着解决大问题的最优策略可以从解决其子问题的最优策略中推导出来。
2. **重叠子问题**:在解决问题的过程中,相同的子问题会多次出现。这是动态规划算法的关键特征,它使得我们可以通过存储子问题的解来避免重复计算。
设计动态规划算法的步骤通常包括:
1. **定义状态**:确定问题的决策空间,每个状态代表问题的一个可能阶段或配置。
2. **定义决策**:识别每个状态可能的下一步动作或决策。
3. **定义价值函数**:确定如何评估每个状态的价值,这通常是目标函数或者成本函数。
4. **构造状态转移方程**:描述从一个状态转移到另一个状态的关系,即如何根据当前状态的决策得到下一个状态的解。
5. **计算初始状态的解**:从最基础的状态开始,逐步计算出所有状态的解。
6. **存储中间结果**:使用记忆化技术,保存已经计算过的子问题解,以便后续使用。
通过一系列应用范例,我们可以更好地理解动态规划的运用:
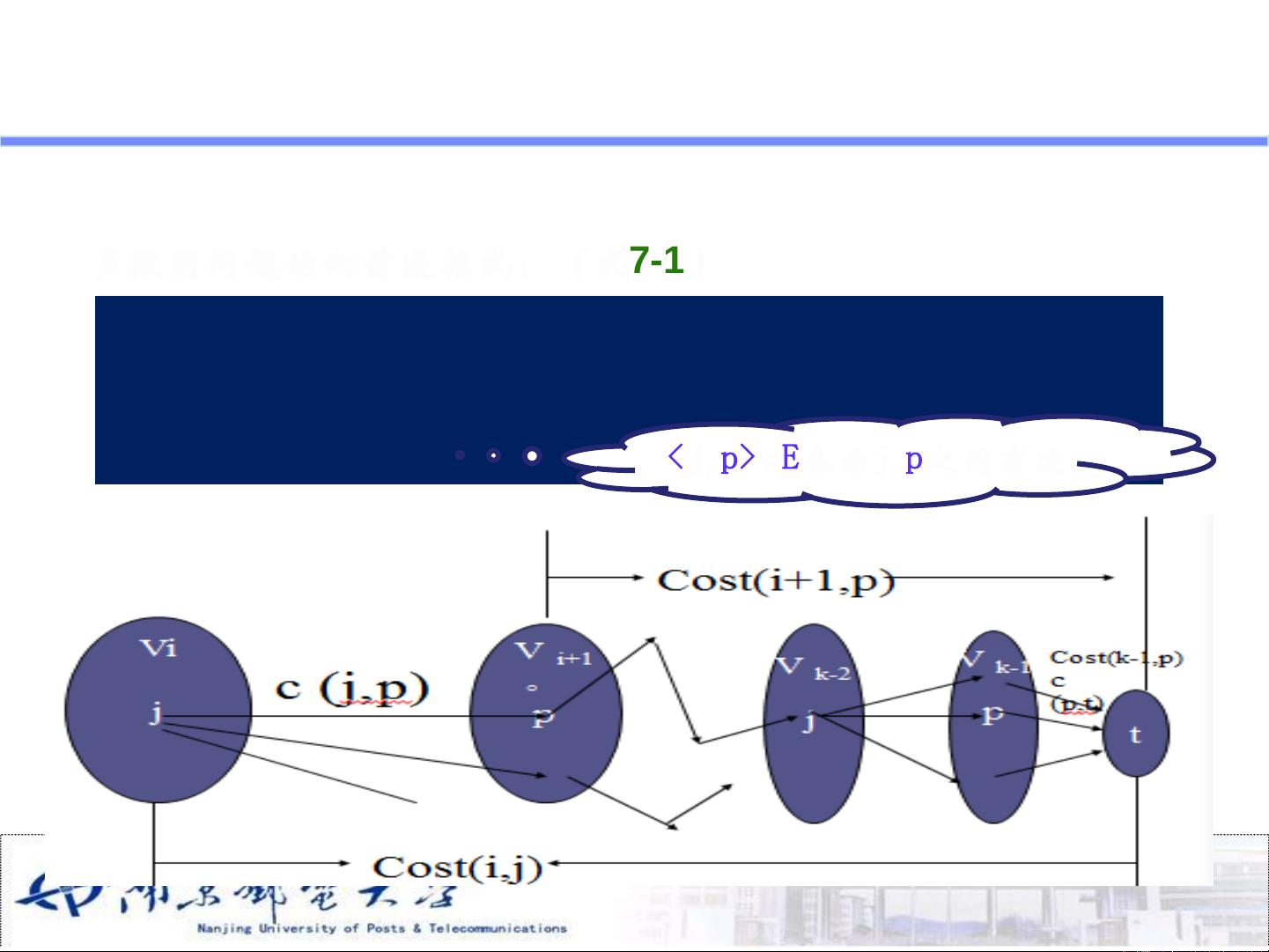
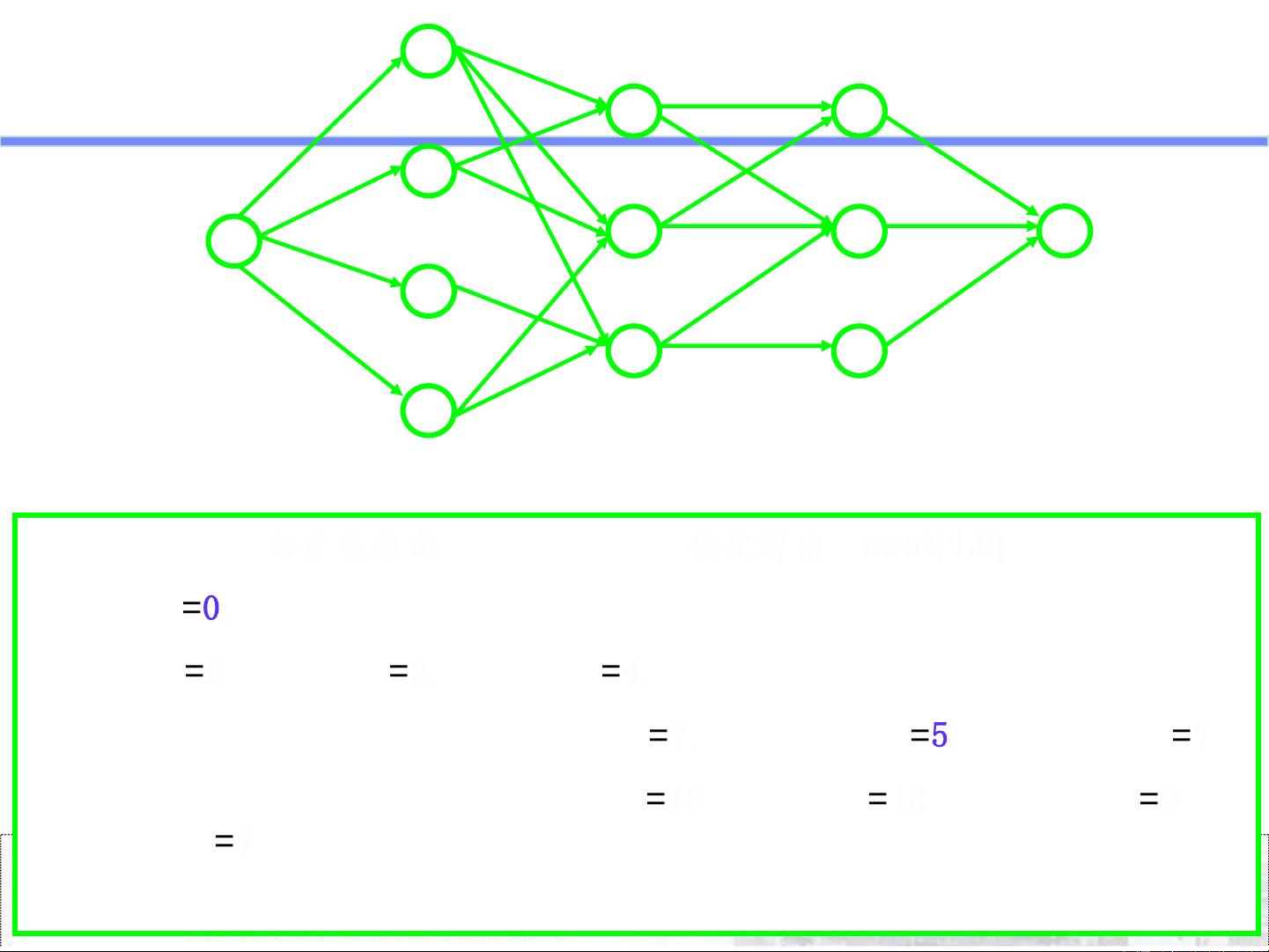
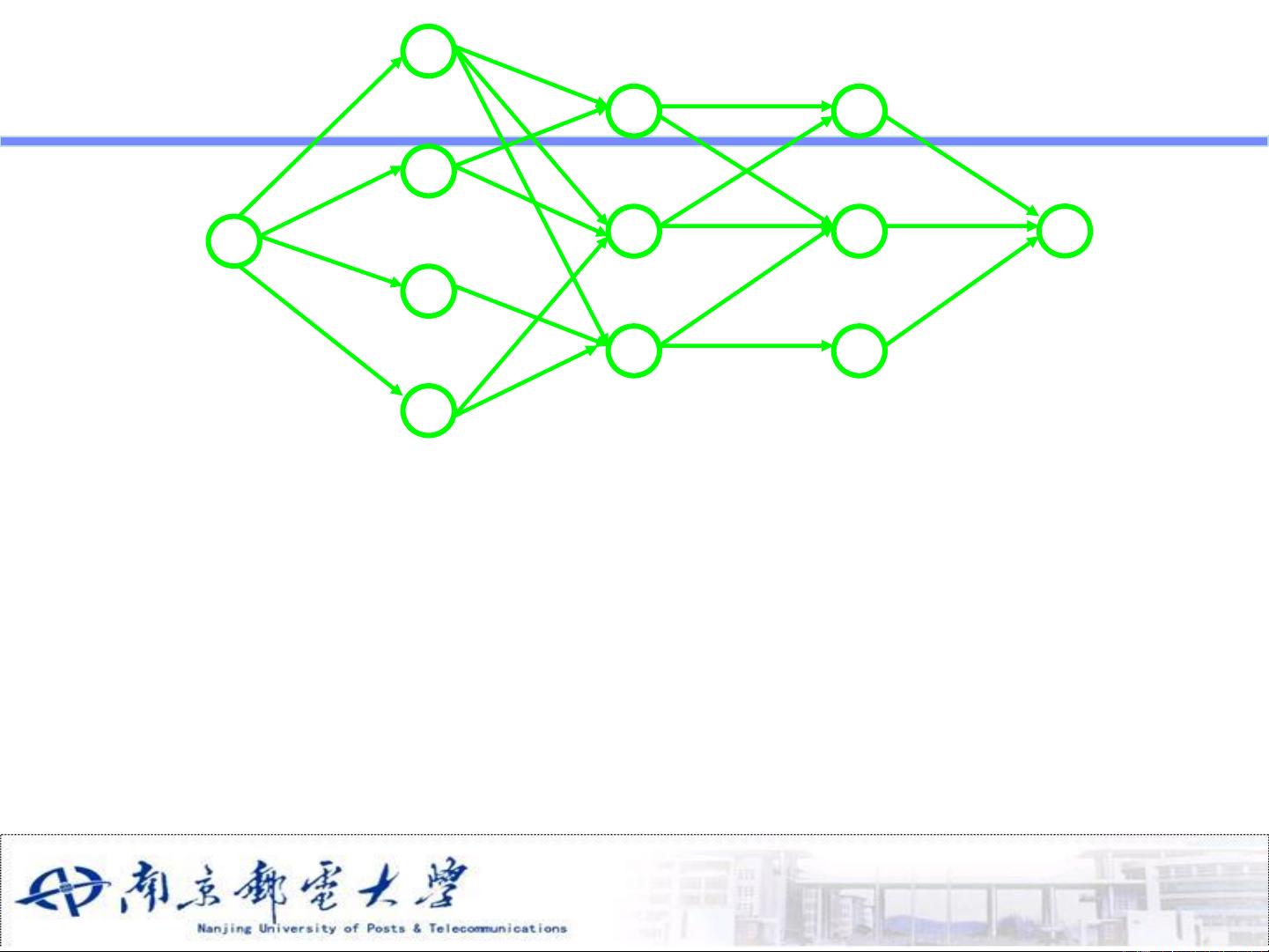
- **多段图问题**:寻找从起点到终点的最短路径,其中路径可能分为多个阶段。
- **每对结点间的最短路径**:如Dijkstra算法或Floyd-Warshall算法,找到图中任意两个节点之间的最短路径。
- **矩阵连乘**:最小化多个矩阵相乘的运算次数,如Strassen算法或Kasami-Wilf算法。
- **最长公共子序列问题**:找到两个序列的最长子序列,该子序列在原序列中分别不需连续但顺序相同。
- **0/1背包问题**:在容量有限的背包中选择物品以最大化总价值,每个物品要么完全放入要么不放。
- **流水作业调度问题**:优化生产流程,安排作业以最小化完成所有作业的总时间。
动态规划与分治法、贪心法的主要区别在于,分治法通常处理的是独立的子问题,而贪心法在每个步骤都采取局部最优解,但不保证全局最优。动态规划则是在考虑全局最优的情况下,通过解决重叠子问题来达到目标。
2013-03-20 上传
170 浏览量
2022-12-15 上传
2011-07-28 上传
2012-08-05 上传
点击了解资源详情
202 浏览量
华亿
- 粉丝: 51
- 资源: 308
最新资源
- dontleaveme:eg恳求用户留在您的网站上。 (愚人节早期的玩笑:clown_face:)
- SC同步法_SC同步_
- python代码自动办公 Excel_案例_把文件夹整理到Excel中项目源码有详细注解,适合新手一看就懂.rar
- linq 转换 sql
- jQuery卡通幸运大转盘特效代码
- crud-react:创建该项目只是为了练习React
- 准网站:Quassel IRC网站的资源,网址为https:quassel-irc.org
- programming-interviews-exposed:书中的实践
- 电脑软件Ansys教程.rar实用
- jishibenaand_java_
- node-tlv:节点电视
- wpstarter:Webpack WordPress入门主题。 可以使用WordPress 5.0+,具有许多很棒的功能,例如自定义徽标,SCSS基础,Webpack支持,自定义程序和小部件开发
- TengineKit_Demo_Identity_Protection
- 图书馆
- python代码自动办公 用Python分析文本数据的词频 项目源码有详细注解,适合新手一看就懂.rar
- jquery tool实现windows桌面效果特效代码