旋转卡壳：凸多边形的对踵点对与经典问题解析

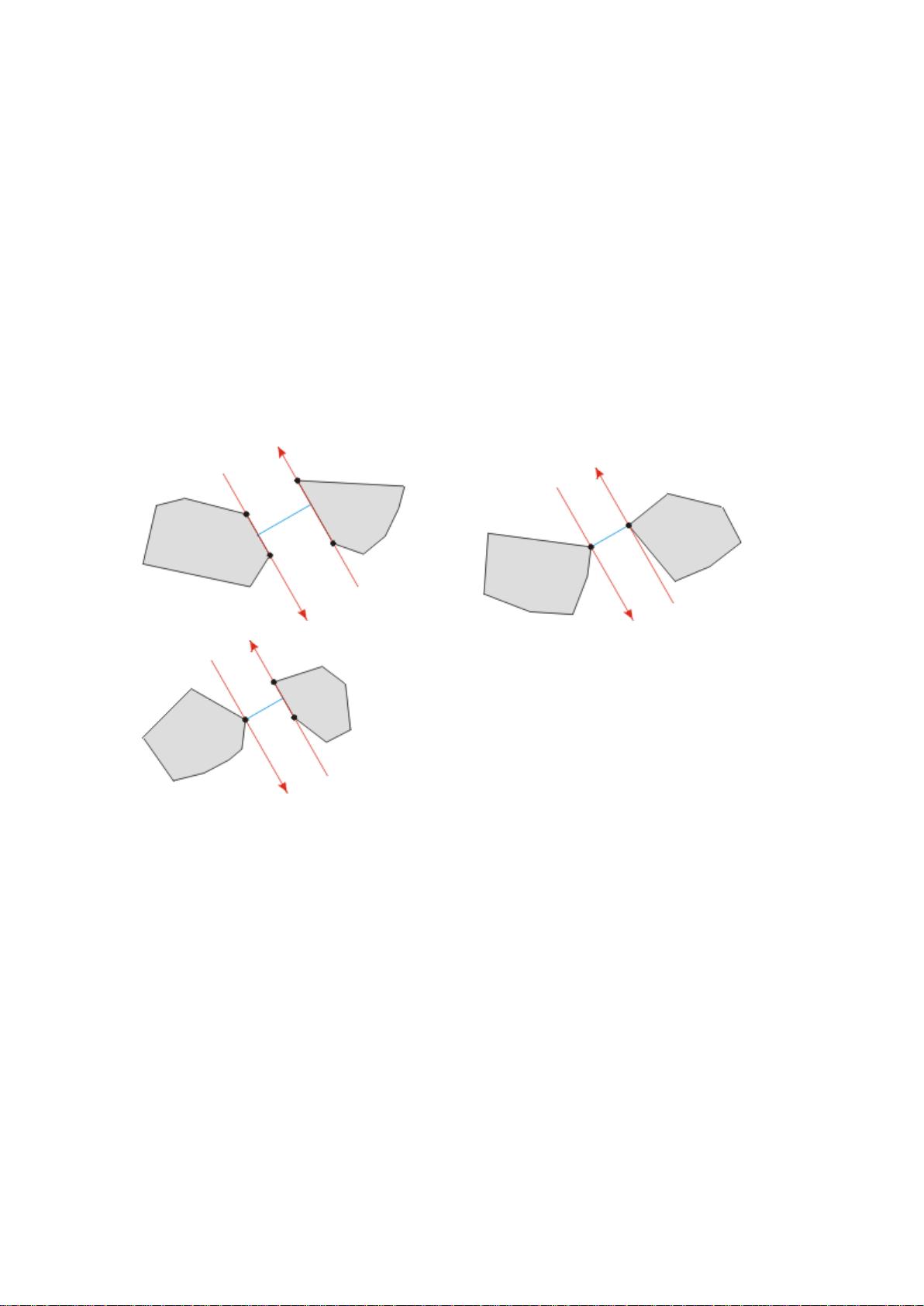
计算几何是计算机科学中研究几何形状与算法之间关系的重要领域，它在图形学、机器人学、地理信息系统等多个应用中扮演关键角色。本文主要聚焦于"旋转卡壳"这一概念，它是以M.I. Shamos在1978年的论文为起点，他在论文中介绍了一个简单但高效的方法来确定凸多边形的直径，即通过比较一对对踵点对的距离来计算。对踵点对指的是两个点p和q，它们位于两条相互平行的切线上，且这两条切线分别与多边形相交于不同的位置。 Shamos的算法是通过围绕多边形旋转一组切片，这些切片类似于一对卡壳，从而得名"旋转卡壳"。这一技术随后被Toussaint在1983年的论文中扩展，用于解决一系列计算几何问题，包括但不限于： 1. 凸多边形的对踵点对：理解这对点如何形成对踵点对，有助于优化多边形的操作，如求直径、宽度、最小/最大距离等。 2. 凸多边形的宽度：测量多边形两侧边界之间的最宽距离，这对于形状分析和变形控制很有价值。 3. 凸多边形间最小/最大距离：计算两个或多边形之间的最短或最长距离，涉及空间布局和碰撞检测等问题。 4. 外接矩形问题：找到凸多边形的最小面积或最小周长的外接矩形，这是尺寸约束和布局设计的关键要素。 5. 三角剖分：如螺旋三角剖分和洋葱三角剖分，是将多边形分割成更小的子形状的过程，对于图形表示和数据结构优化至关重要。 6. 四边形剖分：针对特定的四边形处理方法，可能是分割、裁剪或组合操作。 7. 凸包合并：当多个凸包需要组合或合并时，对踵点对的概念也起到关键作用。 8. 公切线查找：找出多边形共有的切线，这对碰撞检测和图形交互有重要意义。 9. 凸多边形的矢量和和临界切线：涉及多边形的总体动态行为和边界条件的分析。 10. 最薄横截带：研究如何找到穿过多边形的最窄区域，这对路径规划和最优化问题有帮助。 对踵点对在计算几何中是一个核心概念，它不仅提供了求解多边形属性的有效手段，还促进了多项实用算法的发展。通过理解和应用旋转卡壳原理，可以大大提高处理复杂几何形状问题的效率。